上海市奉贤区2022年九年级中考数学二模试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 如果实数a与3互为相反数,那么a是( )A、 B、 C、3 D、2. 的计算结果是( )A、2 B、3 C、 D、3. 据2022年北京冬奥会新闻发言人透露,中国大陆地区约316000000人次收看了冬奥会的开幕式.数据316000000用科学记数法表示为( )A、 B、 C、 D、4. 小明为了解本班同学一周课外书的阅读量,随机抽取班上20名同学进行调查,调查结果如下表,那么这20名同学该周课外书阅读量的平均数是( )
阅读量(本/周)
0
1
2
3
4
人数
2
5
4
5
4
A、2本 B、2.2本 C、3本 D、3.2本5. 如图,在中, , 点D在边的延长线上,根据图中尺规作图的痕迹,可知的度数为( ) A、 B、 C、 D、6. 如果一个矩形经过一个多边形的各顶点,那么我们把这个矩形叫做这个多边形的外接矩形.如图,矩形是正六边形的外接矩形,如果正六边形的边长为2,那么矩形长边与短边的比是( )
A、 B、 C、 D、6. 如果一个矩形经过一个多边形的各顶点,那么我们把这个矩形叫做这个多边形的外接矩形.如图,矩形是正六边形的外接矩形,如果正六边形的边长为2,那么矩形长边与短边的比是( )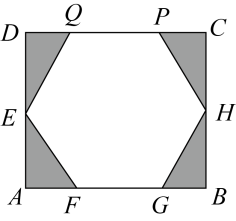 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. -27的立方根是.8. 如果单项式与是同类项,那么的值是 .9. 因式分解: .10. 已知函数 , 那么 .11. 有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…6点的标记,掷一次骰子,向上的一面出现的点数是2的倍数的概率是 .12. 某眼镜店暑假期间开展学生配镜优惠活动.某款式眼镜的广告如图,那么广告牌上填的原价是元.
 13. 如果关于 是方程 有两个相等的实数根,那么 的值等于 .14. 甲、乙两地4月下旬的日平均气温统计图如图所示,那么由图中信息可知甲、乙两地这10天日平均气温比较稳定的是 . (填“甲”或“乙”)
13. 如果关于 是方程 有两个相等的实数根,那么 的值等于 .14. 甲、乙两地4月下旬的日平均气温统计图如图所示,那么由图中信息可知甲、乙两地这10天日平均气温比较稳定的是 . (填“甲”或“乙”) 15. 在梯形中,AB//CD, , E是腰的中点,联结 . 如果设 , 那么(含、的式子表示)16. 如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA ,则BD的长度为 .
15. 在梯形中,AB//CD, , E是腰的中点,联结 . 如果设 , 那么(含、的式子表示)16. 如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA ,则BD的长度为 .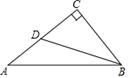 17. 如图,在等边中, , 如果以为直径的和以A为圆心的相切,那么的半径r的值是 .
17. 如图,在等边中, , 如果以为直径的和以A为圆心的相切,那么的半径r的值是 . 18. 如图,在矩形中, , 点E在边上,联结 , 将矩形沿所在直线翻折,点D的对应点为P,联结 . 如果 , 那么的长度是 .
18. 如图,在矩形中, , 点E在边上,联结 , 将矩形沿所在直线翻折,点D的对应点为P,联结 . 如果 , 那么的长度是 .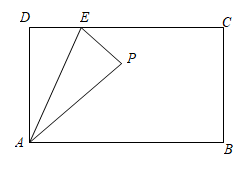
三、解答题
-
19. 先化简,再求值: ,其中 .20. 解方程21. 如图,在平面直角坐标系中,的边在x轴正半轴上, , , C为斜边的中点,反比例函数在第一象限内的图像经过点C,交边于点D.
 (1)、这个反比例函数的解析式;(2)、连结 , 求的值.22. 图1是某种型号圆形车载手机支架,由圆形钢轨、滑动杆、支撑杆组成.图2是它的正面示意图,滑动杆的两端都在圆O上,A、B两端可沿圆形钢轨滑动,支撑杆的底端C固定在圆O上,另一端D是滑动杆的中点,(即当支架水平放置时直线平行于水平线,支撑杆垂直于水平线),通过滑动A、B可以调节的高度.当经过圆心O时,它的宽度达到最大值 , 在支架水平放置的状态下:
(1)、这个反比例函数的解析式;(2)、连结 , 求的值.22. 图1是某种型号圆形车载手机支架,由圆形钢轨、滑动杆、支撑杆组成.图2是它的正面示意图,滑动杆的两端都在圆O上,A、B两端可沿圆形钢轨滑动,支撑杆的底端C固定在圆O上,另一端D是滑动杆的中点,(即当支架水平放置时直线平行于水平线,支撑杆垂直于水平线),通过滑动A、B可以调节的高度.当经过圆心O时,它的宽度达到最大值 , 在支架水平放置的状态下: (1)、当滑动杆的宽度从10厘米向上升高调整到6厘米时,求此时支撑杆的高度.(2)、如图3,当某手机被支架锁住时,锁住高度与手机宽度恰好相等(),求该手机的宽度.23. 已知:如图,在矩形中,点E在边的延长线上, , 连接 , 分别交边、对角线于点F、G, .
(1)、当滑动杆的宽度从10厘米向上升高调整到6厘米时,求此时支撑杆的高度.(2)、如图3,当某手机被支架锁住时,锁住高度与手机宽度恰好相等(),求该手机的宽度.23. 已知:如图,在矩形中,点E在边的延长线上, , 连接 , 分别交边、对角线于点F、G, . (1)、求证:;(2)、求证: .
(1)、求证:;(2)、求证: .

