山东省2023届高考数学考向核心卷
试卷更新日期:2023-03-10 类型:高考模拟
一、单选题
-
1. 已知集合 , 集合 , 则( )A、 B、 C、 D、2. 若复数z满足 , 则复数z的虚部为( )A、 B、 C、 D、3. 已知向量 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 如图,用、、三类不同的元件连接成一个系统,当正常工作且、至少有一个正常工作时,系统正常工作,已知、、正常工作的概率依次是、、 , 已知在系统正常工作的前提下,求只有和正常工作的概率是( )
 A、 B、 C、 D、5. 已知数列 为等差数列,首项 ,若 ,则使得 的n的最大值为( )A、2007 B、2008 C、2009 D、20106. 已知函数的部分图象如图所示,( )
A、 B、 C、 D、5. 已知数列 为等差数列,首项 ,若 ,则使得 的n的最大值为( )A、2007 B、2008 C、2009 D、20106. 已知函数的部分图象如图所示,( )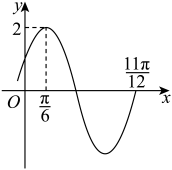 A、 B、-1 C、 D、7. 若正实数、满足 , 且不等式有解,则实数的取值范围是( ).A、或 B、或 C、 D、8. 记 , 设函数 , 若函数恰有三个零点,则实数的取值范围的是( )A、 B、 C、 D、
A、 B、-1 C、 D、7. 若正实数、满足 , 且不等式有解,则实数的取值范围是( ).A、或 B、或 C、 D、8. 记 , 设函数 , 若函数恰有三个零点,则实数的取值范围的是( )A、 B、 C、 D、二、多选题
-
9. 某医院派出甲、乙、丙、丁4名医生到 , , 三家企业开展“新冠肺炎”防护排查工作,每名医生只能到一家企业工作,则下列结论正确的是( )A、所有不同分派方案共种 B、若每家企业至少分派1名医生,则所有不同分派方案共36种 C、若每家企业至少派1名医生,且医生甲必须到企业,则所有不同分派方案共12种 D、若企业最多派1名医生,则所有不同分派方案共48种10. 已知是的导函数,且 , 则( )A、 B、 C、的图象在处的切线的斜率为0 D、在上的最小值为111. 如图1,在菱形ABCD中, , , 将沿AC折起,使点B到达点P的位置,形成三棱锥 , 如图2.在翻折的过程中,下列结论正确的是( )
 A、 B、三棱锥体积的最大值为3 C、存在某个位置,使 D、若平面平面ACD,则直线AD与平面PCD所成角的正弦值为12. 已知点 , , , 抛物线 . 过点的直线与交于 , 两点,直线分别与交于另一点 , 则下列说法中正确的是( )A、 B、直线的斜率为 C、若的面积为(为坐标原点),则与的夹角为 D、若为抛物线上位于轴上方的一点, , 则当取最大值时,的面积为2
A、 B、三棱锥体积的最大值为3 C、存在某个位置,使 D、若平面平面ACD,则直线AD与平面PCD所成角的正弦值为12. 已知点 , , , 抛物线 . 过点的直线与交于 , 两点,直线分别与交于另一点 , 则下列说法中正确的是( )A、 B、直线的斜率为 C、若的面积为(为坐标原点),则与的夹角为 D、若为抛物线上位于轴上方的一点, , 则当取最大值时,的面积为2三、填空题
-
13. 已知函数 , 过点作曲线的切线 , 则的方程为.14. 已知 , 则.(用数字作案)15. 已知函数 , 若对任意实数 , 恒有 , 则 .16. 已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,且平面ABCD, , 点M为线段PC上的动点(不包含端点),则当三棱锥的外接球的表面积最小时,CM的长为.
四、解答题
-
17. 已知等比数列 的前n项和为 ,且 .(1)、求 与 ;(2)、记 ,求数列 的前n项和 .18. 在① , ② , ③ , . 这三个条件中任进一个,补充在下面问题中并作答.
已知中,内角所对的边分别为 , 且____.
(1)、求的值;(2)、若 , 求的周长与面积.19. 由中央电视台综合频道(CCTV-1)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到了青年观众的喜爱.为了了解观众对节目的喜爱程度,电视台随机调查了A,B两个地区的100名观众,得到如下所示的2×2列联表.非常喜欢
喜欢
合计
A
30
15
B
x
y
合计
已知在被调查的100名观众中随机抽取1名,该观众来自B地区且喜爱程度为“非常喜欢”的概率为0.35.
附: , ,
0.05
0.010
0.001
3.841
6.635
10.828
(1)、现从100名观众中根据喜爱程度用分层抽样的方法抽取20名进行问卷调查,则应抽取喜爱程度为“非常喜欢”的A,B地区的人数各是多少?(2)、完成上述表格,并根据表格判断是否有95%的把握认为观众的喜爱程度与所在地区有关系.(3)、若以抽样调查的频率为概率,从A地区随机抽取3人,设抽到喜爱程度为“非常喜欢”的观众的人数为X,求X的分布列和期望.
