辽宁省盘锦市盘山县2022年九年级第二次模拟考试数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. -2021的相反数是( )A、2021 B、-2021 C、 D、2. 如图是由若干个完全相同的立方体搭成的几何体,该几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算中,正确的是( )A、 B、 C、 D、4. 下列图案中是中心对称图形但不是轴对称图形的是( )A、
3. 下列计算中,正确的是( )A、 B、 C、 D、4. 下列图案中是中心对称图形但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下面统计调查中,适合采用全面调查的是( )A、调查市场上某种食品防腐剂是否符合国家标准 B、调查某城市初中生每周“诵读经典”的时间 C、对某品牌手机的防水性能的调查 D、疫情期间对国外入境人员的核酸检测6. 不等式组的解集表示在数轴上,正确的是( )A、
5. 下面统计调查中,适合采用全面调查的是( )A、调查市场上某种食品防腐剂是否符合国家标准 B、调查某城市初中生每周“诵读经典”的时间 C、对某品牌手机的防水性能的调查 D、疫情期间对国外入境人员的核酸检测6. 不等式组的解集表示在数轴上,正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 网上购物已经成为人们常用的一种购物方式.购物方式的改变给快递行业带来了商机,也带来了挑战.为了提高效率,某快递公司研发了快递机器人专门负责分拣包裹,已知单个机器人比人工(一个人)每小时多分拣100个,单个机器人分拣9000个包裹和人工(一个人)分拣6000个包裹所用时间相同.设人工(一个人)每小时分拣x个包裹,则可列方程为( )A、 B、 C、 D、8. 如图,直线l的解析式为 , 它与x轴和y轴分别相交于A,B两点,点C为线段上一动点,过点C作直线l的平行线m,交y轴于点D,点C从原点O出发,沿以每秒个单位长度的速度向终点A运动,运动时间为t秒,以为斜边作等腰直角三角形(E,O两点分别在两侧).若和的重合部分的面积为S,则S与t之间的函数关系图象大致是( )
7. 网上购物已经成为人们常用的一种购物方式.购物方式的改变给快递行业带来了商机,也带来了挑战.为了提高效率,某快递公司研发了快递机器人专门负责分拣包裹,已知单个机器人比人工(一个人)每小时多分拣100个,单个机器人分拣9000个包裹和人工(一个人)分拣6000个包裹所用时间相同.设人工(一个人)每小时分拣x个包裹,则可列方程为( )A、 B、 C、 D、8. 如图,直线l的解析式为 , 它与x轴和y轴分别相交于A,B两点,点C为线段上一动点,过点C作直线l的平行线m,交y轴于点D,点C从原点O出发,沿以每秒个单位长度的速度向终点A运动,运动时间为t秒,以为斜边作等腰直角三角形(E,O两点分别在两侧).若和的重合部分的面积为S,则S与t之间的函数关系图象大致是( )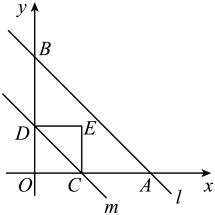 A、
A、 B、
B、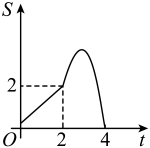 C、
C、 D、
D、
二、填空题
-
9. 代数式有意义,则x的取值范围是 .10. 分解因式:11. 一个扇形的半径为 ,圆心角为 ,则它的面积为 .12. 如图,将直角三角板ABC放在平面直角坐标系中,点A,B的坐标分别为(2,1),(7,1),将三角板ABC沿x轴正方向平移,点B的对应点B'刚好落在反比例函数y=(x>0)的图象上,则点C平移的距离CC'= .
 13. 如图,线段 , 于点A,于点B, , , 点P为线段上一动点,且以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似,则的长为 .
13. 如图,线段 , 于点A,于点B, , , 点P为线段上一动点,且以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似,则的长为 . 14. 如图,在中,是的中点,则中最短边的长度为 .
14. 如图,在中,是的中点,则中最短边的长度为 .
三、解答题
-
15. 先化简,再求值: ,其中 .16. 为了增强学生疫情防控意识,某校组织了一次“疫情防控知识”专题学习,并进行了一次全校1200名学生都参加的测试,阅卷后,从中随机抽取了部分学生的答卷进行统计分析,并绘制了如图所示的两幅不完整的统计图,请结合图中给出的信息解答下列问题:

 (1)、在扇形统计图中m的值为 , 在“90-100”这组所对应的圆心角的度数为;(2)、请你将条形统计图补充完整;(3)、根据抽样调查的结果,请你估计该校1200名学生中有多少名学生成绩不低于80分?17. 四张正面分别写有数字:-2,-1,0,1的卡片,它们的背面完全相同,现将这四张卡片背面朝上洗匀.(1)、从中任意抽取一张卡片,则所抽卡片上数字为负数的概率是;(2)、先从中任意抽取一张卡片,以其正面数字作为x的值,然后再从剩余的卡片中随机抽一张,以其正面的数字作为y的值,请用列表法或树状图法,求点 在第二象限的概率.18. “青山绿水,生态农业”.某地需引水修建水库,既可蓄水灌溉,又可美化环境.据了解,水库C修建在水源A的正东方向,在水源A的北偏东方向有一古迹B,B与A相距 , 其中水库C在古迹B的东南方向.
(1)、在扇形统计图中m的值为 , 在“90-100”这组所对应的圆心角的度数为;(2)、请你将条形统计图补充完整;(3)、根据抽样调查的结果,请你估计该校1200名学生中有多少名学生成绩不低于80分?17. 四张正面分别写有数字:-2,-1,0,1的卡片,它们的背面完全相同,现将这四张卡片背面朝上洗匀.(1)、从中任意抽取一张卡片,则所抽卡片上数字为负数的概率是;(2)、先从中任意抽取一张卡片,以其正面数字作为x的值,然后再从剩余的卡片中随机抽一张,以其正面的数字作为y的值,请用列表法或树状图法,求点 在第二象限的概率.18. “青山绿水,生态农业”.某地需引水修建水库,既可蓄水灌溉,又可美化环境.据了解,水库C修建在水源A的正东方向,在水源A的北偏东方向有一古迹B,B与A相距 , 其中水库C在古迹B的东南方向. (1)、若在水源A与水库C之间修建一条水渠,求该水渠的最短长度.(2)、在古迹B的西南方向处有一古墓群,为了保护文物,不破坏古墓,在古墓群周围范围内不得进行任何土工作业,判断按照(1)中的方式修建水渠是否合理,并说明理由.(结果保留一位小数.参考数据: , , )19. 某特产店出售大米,一天可销售20袋,每袋可盈利40元,为了扩大销售,增加盈利,尽快减少库存,决定采取降价措施,据统计发现,若每袋降价2元,平均每天可多售4袋.(1)、设每袋大米降价为x(x为偶数)元时,利润为y元,写出y与x的函数关系式.(2)、若每天盈利1200元,则每袋应降价多少元?(3)、每袋大米降价多少元时,商店可获最大利润?最大利润是多少?20. 如图1,已知抛物线与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为D, .
(1)、若在水源A与水库C之间修建一条水渠,求该水渠的最短长度.(2)、在古迹B的西南方向处有一古墓群,为了保护文物,不破坏古墓,在古墓群周围范围内不得进行任何土工作业,判断按照(1)中的方式修建水渠是否合理,并说明理由.(结果保留一位小数.参考数据: , , )19. 某特产店出售大米,一天可销售20袋,每袋可盈利40元,为了扩大销售,增加盈利,尽快减少库存,决定采取降价措施,据统计发现,若每袋降价2元,平均每天可多售4袋.(1)、设每袋大米降价为x(x为偶数)元时,利润为y元,写出y与x的函数关系式.(2)、若每天盈利1200元,则每袋应降价多少元?(3)、每袋大米降价多少元时,商店可获最大利润?最大利润是多少?20. 如图1,已知抛物线与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为D, . (1)、求抛物线的函数表达式;(2)、判断的形状并说明理由;(3)、如图2,N是AC下方的抛物线上的一个动点,且点N的横坐标为n,求面积S与n的函数关系式及S的最大值;(4)、在抛物线上是否存在一点N,使得 , 若存在,请直接写出点N的坐标若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、判断的形状并说明理由;(3)、如图2,N是AC下方的抛物线上的一个动点,且点N的横坐标为n,求面积S与n的函数关系式及S的最大值;(4)、在抛物线上是否存在一点N,使得 , 若存在,请直接写出点N的坐标若不存在,请说明理由.