辽宁省鞍山市2022年中考数学模拟试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
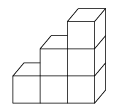
1. 下列运算正确的是( )A、 =±3 B、(﹣2)3=8 C、﹣22=﹣4 D、﹣|﹣3|=32. 如图是由6个完全相同的小正方体搭建而成的几何体,则这个几何体的主视图是( )
 A、
A、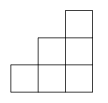 B、
B、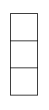 C、
C、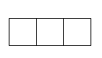 D、
D、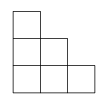 3. 计算所得的结果是( )A、 B、 C、 D、4. 一组数据为5,6,7,8,10,10,某同学在抄题时,误把其中一个10抄成了100,那么该同学所抄的数据和原数据相比,不变的统计量是( )A、中位数 B、平均数 C、方差 D、众数5. 已知等腰三角形的周长为15cm,一边长为7cm,则该等腰三角形的底边长为( )A、5 cm B、3cm或5 cm C、3 cm D、1 cm或7 cm6. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
3. 计算所得的结果是( )A、 B、 C、 D、4. 一组数据为5,6,7,8,10,10,某同学在抄题时,误把其中一个10抄成了100,那么该同学所抄的数据和原数据相比,不变的统计量是( )A、中位数 B、平均数 C、方差 D、众数5. 已知等腰三角形的周长为15cm,一边长为7cm,则该等腰三角形的底边长为( )A、5 cm B、3cm或5 cm C、3 cm D、1 cm或7 cm6. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( ) A、 B、6 C、4 D、57. 如图1,中, , D,E分别是的中点,点P沿从点B运动到点C,设B,P两点间的距离为x, , 图2是点P运动时y随x变化的关系图象,则的面积为( )
A、 B、6 C、4 D、57. 如图1,中, , D,E分别是的中点,点P沿从点B运动到点C,设B,P两点间的距离为x, , 图2是点P运动时y随x变化的关系图象,则的面积为( ) A、 B、 C、6 D、98. 下列说法正确的是( )A、所有的等边三角形是全等形 B、面积相等的三角形是全等三角形 C、到三角形三边距离相等的点是三边中线的交点 D、到三角形三个顶点距离相等的是三边中垂线的交点
A、 B、 C、6 D、98. 下列说法正确的是( )A、所有的等边三角形是全等形 B、面积相等的三角形是全等三角形 C、到三角形三边距离相等的点是三边中线的交点 D、到三角形三个顶点距离相等的是三边中垂线的交点二、填空题
-
9. 据统计,全球每小时约吨污水排入江湖河流,精确到百万位表示为: .10. 在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有个.11. 辽宁省将在2020年底前实现县城以上城区5G全覆盖.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,求这两种网络的峰值速率.设5G网络的峰值速率为每秒传输x兆数据,依题意列方程为.12. 如图,在平行四边形中, , , M是边的中点,若线段绕点M旋转得到线段 , 如图,连接 , 则长度的最小值是 .
 13. 设O是四边形ABCD的对角线AC、BD的交点,若∠BAD+∠ACB=180°,且BC=3,AD=4,AC=5,AB=6.则 = .
13. 设O是四边形ABCD的对角线AC、BD的交点,若∠BAD+∠ACB=180°,且BC=3,AD=4,AC=5,AB=6.则 = . 14. 如图,为的直径,点D是弧的中点,过点D作于点E,延长交于点F,若 , , 则的直径长为 .
14. 如图,为的直径,点D是弧的中点,过点D作于点E,延长交于点F,若 , , 则的直径长为 . 15. 如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1 ,
15. 如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1 ,再以BE为对角线作第三个正方形EFBO2 , 如此作下去,…,则所作的第n个正方形的面积Sn=.

三、解答题
-
16. 先化简,再求值: , 且x为满足的整数.17. 如图,已知点在双曲线上,点B、D在双曲线上,轴.
 (1)、当 , , 时,求此时点A的坐标;(2)、若点A、C关于原点O对称,试判断四边形的形状,并说明理由18.
(1)、当 , , 时,求此时点A的坐标;(2)、若点A、C关于原点O对称,试判断四边形的形状,并说明理由18.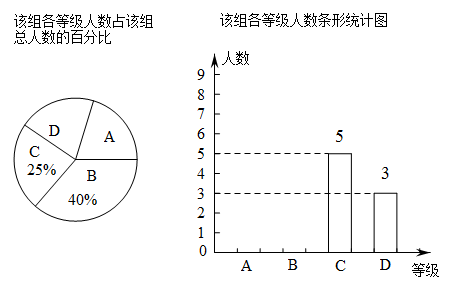 (1)、求D等级所对扇形的圆心角,并将条形统计图补充完整;(2)、该组达到A等级的同学中只有1位男同学,杨老师打算从该组达到A等级的同学中随机选出2位同学在全班介绍经验,请用列表法或画树状图的方法,求出所选两位同学恰好是1位男同学和1位女同学的概率.19. 小明、小芳做一个“配色”的游戏.右图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.
(1)、求D等级所对扇形的圆心角,并将条形统计图补充完整;(2)、该组达到A等级的同学中只有1位男同学,杨老师打算从该组达到A等级的同学中随机选出2位同学在全班介绍经验,请用列表法或画树状图的方法,求出所选两位同学恰好是1位男同学和1位女同学的概率.19. 小明、小芳做一个“配色”的游戏.右图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负. (1)、利用列表或树状图的方法表示此游戏所有可能出现的结果;(2)、此游戏的规则,对小明、小芳公平吗?试说明理由.20. 如图,双曲线经过点 , 且与直线有两个不同的交点.
(1)、利用列表或树状图的方法表示此游戏所有可能出现的结果;(2)、此游戏的规则,对小明、小芳公平吗?试说明理由.20. 如图,双曲线经过点 , 且与直线有两个不同的交点.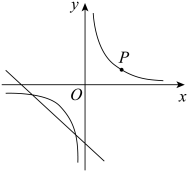 (1)、求m的值.(2)、求k的取值范围.21. 已知将成本为40元的某种商品按50元的定价售出时,能卖出500个,如果该种商品每涨价1元,其销售量就要减少20个,如何定价才能获得最大收益?22. 如图,一楼房AB后有一小山坡,其坡度为: , 山坡面上一点E处有一亭子,测得坡脚C与楼房的水平距离米,与亭子的距离米,小张从楼房测得E点的俯角为 , 求楼房的高度.
(1)、求m的值.(2)、求k的取值范围.21. 已知将成本为40元的某种商品按50元的定价售出时,能卖出500个,如果该种商品每涨价1元,其销售量就要减少20个,如何定价才能获得最大收益?22. 如图,一楼房AB后有一小山坡,其坡度为: , 山坡面上一点E处有一亭子,测得坡脚C与楼房的水平距离米,与亭子的距离米,小张从楼房测得E点的俯角为 , 求楼房的高度.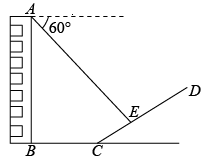 23. 如图,正方形中,点E,F,G分别为边 , , 上的点,且 , 连接 , , .
23. 如图,正方形中,点E,F,G分别为边 , , 上的点,且 , 连接 , , .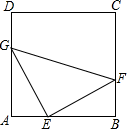 (1)、可以看成是绕点M逆时针旋转角所得,请在图中画出点M,并直接写出角的度数;(2)、当点E位于何处时,的面积取得最小值?请说明你的理由;(3)、试判断直线与外接圆的位置关系,并说明你的理由.24. 如图,为直径,C,D为上不同于A、B的两点,过点C作 , 垂足为E,直线与相交于F点.
(1)、可以看成是绕点M逆时针旋转角所得,请在图中画出点M,并直接写出角的度数;(2)、当点E位于何处时,的面积取得最小值?请说明你的理由;(3)、试判断直线与外接圆的位置关系,并说明你的理由.24. 如图,为直径,C,D为上不同于A、B的两点,过点C作 , 垂足为E,直线与相交于F点.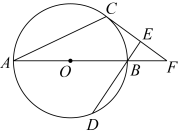 (1)、试说明:为的切线;(2)、若 , , 求的长.25. 如图1,平面直角坐标系xOy中,抛物线与x轴分则点A和点 , 与y轴交于点C,对称轴为直线 , 且 , P为抛物线上一动点.
(1)、试说明:为的切线;(2)、若 , , 求的长.25. 如图1,平面直角坐标系xOy中,抛物线与x轴分则点A和点 , 与y轴交于点C,对称轴为直线 , 且 , P为抛物线上一动点.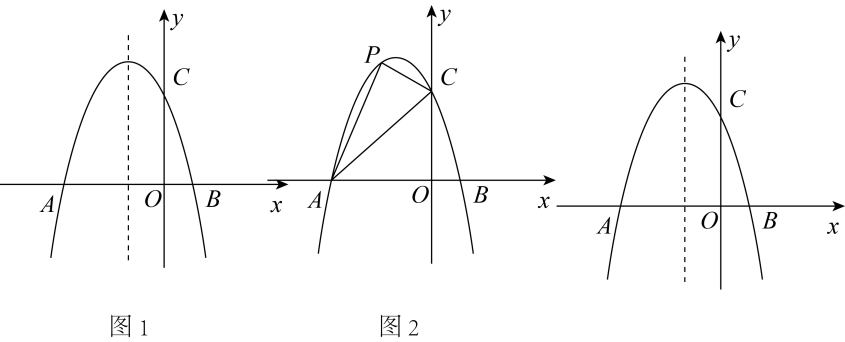 (1)、直接写出抛物线的解析式;(2)、如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;(3)、设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.
(1)、直接写出抛物线的解析式;(2)、如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;(3)、设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.