辽宁省名校联盟2022-2023学年高三下学期数学质量检测考试试卷
试卷更新日期:2023-03-10 类型:高考模拟
一、单选题
-
1. 复数在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知集合 , , 则( )A、 B、 C、 D、3. 某地有9个快递收件点,在某天接收到的快递个数分别为360,284,290,300,402,188,240,260,288,则这组数据的第72百分位数为( )A、290 B、295 C、300 D、3304. “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知单位向量 , , 若对任意实数 , 恒成立,则向量 , 的夹角的取值范围为( )A、 B、 C、 D、6. 已知函数的最小正周期为 , 设 , , , 则( )A、 B、 C、 D、7. 在平面中,若正内切圆的面积为 , 内切圆与外接圆之间的圆环面积为 , 则在空间中,若正四面体内切球的体积为 , 内切球之外与外接球之内的几何体的体积为 , 则( )A、 B、 C、 D、8. 从商业化书店到公益性城市书房,再到“会呼吸的文化森林”——图书馆,建设高水平、现代化、开放式的图书馆一直以来是大众的共同心声.现有一块不规则的地,其平面图形如图1所示,(百米),建立如图2所示的平面直角坐标系,将曲线看成函数图象的一部分,为一次函数图象的一部分,若在此地块上建立一座图书馆,平面图为直角梯形(如图2),则图书馆占地面积(万平方米)的最大值为( )
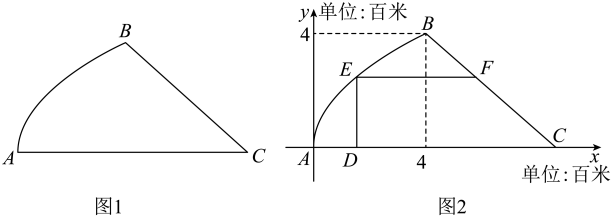 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 在正方体中,E,F分别为 , 的中点,则下列结论错误的是( )A、平面 B、平面 C、平面 D、平面10. 设均为正数,且 , 则( )A、 B、当时,可能成立 C、 D、11. 已知函数 , 则( )A、是奇函数 B、当时, C、的最大值是1 D、的图象关于直线对称12. 已知F是抛物线的焦点,点在抛物线W上,过点F的两条互相垂直的直线 , 分别与抛物线W交于B,C和D,E,过点A分别作 , 的垂线,垂足分别为M,N,则( )A、四边形面积的最大值为2 B、四边形周长的最大值为 C、为定值 D、四边形面积的最小值为32
三、填空题
-
13. 某容器内液体的高度单位:与时间单位:的函数关系式为 , 则当时,液体高度的瞬时变化率为14. 的展开式中,项的系数为 .15. 若数列是等比数列且 , , , 则.16. 为椭圆上一点,曲线与坐标轴的交点为 , , , , 若 , 则到轴的距离为.
四、解答题
-
17. 已知的内角 , , 的对边分别为 , , , 且 , .(1)、求的大小;(2)、若 , 求边上高的长度.18. 在① , ②这两个条件中选一个合适的补充在下面的横线上,使得问题可以解答,并写出完整的解答过程.
问题:在各项均为整数的等差数列中, , 公差为 , 且____.
(1)、求的通项公式;(2)、若 , 求数列的前n项和.19. 口袋中有5个球,其中白球2个,黑球3个,每次从口袋中取一个球,若取出的是白球,则不放回,若取出的是黑球,则放回袋中.(1)、求在第2次取出的是黑球的条件下,第1次取出的是白球的概率;(2)、求取了3次后,取出的白球的个数的分布列及数学期望.