河南省郑州市2023届高三理数第一次质量预测试卷
试卷更新日期:2023-03-10 类型:高考模拟
一、单选题
-
1. 设集合 , . 则( )A、 B、 C、 D、2. 已知是虚数单位,若复数的实部为1, , 则复数的虚部为( )A、或 B、或 C、或1 D、或3. 已知双曲线()的离心率为 , 则该双曲线的渐近线方程为A、 B、 C、 D、4. 欧拉函数的函数值等于所有不超过正整数 , 且与互素(也称互质)的正整数的个数,例如 , , . 则( )A、数列单调 B、 C、数列是等比数列 D、5. 若实数 , 满足约束条件 , 则的( )A、最大值为4 B、最小值为4 C、最大值为5 D、最小值为56. 设等差数列的前项和为 , , , 则公差的取值范围是( )A、 B、 C、 D、7. 记函数的最小正周期为 . 若 , 且的图象的一条对称轴为 , 关于该函数有下列四个说法:
①;
②;
③在上单调递增;
④为了得到的图象,只需将的图象向右平移个单位长度.
以上四个说法中,正确的个数为( )
A、1 B、2 C、3 D、48. 河南博物院主展馆的主体建筑以元代登封古观星台为原型,经艺术夸张演绎成“戴冠的金字塔”造型,冠部为“方斗”形,上扬下覆,取上承“甘露”、下纳“地气”之意.冠部以及冠部下方均可视为正四棱台.已知一个“方斗”的上底面与下底面的面积之比为 , 高为2,体积为 , 则该“方斗”的侧面积为( ) A、24 B、12 C、 D、9. 记的内角 , , 的对边分别为 , , , 已知角 , , 则角( )A、 B、 C、 D、10. 在如图所示的实验装置中,两个正方形框架 , 的边长都为1,且它们所在的平面互相垂直.活动弹子 , 分别在正方形对角线和上移动,且和的长度保持相等,记 . 则下列结论错误的是( )
A、24 B、12 C、 D、9. 记的内角 , , 的对边分别为 , , , 已知角 , , 则角( )A、 B、 C、 D、10. 在如图所示的实验装置中,两个正方形框架 , 的边长都为1,且它们所在的平面互相垂直.活动弹子 , 分别在正方形对角线和上移动,且和的长度保持相等,记 . 则下列结论错误的是( )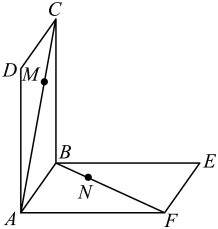 A、该模型外接球的半径为 B、当时,的长度最小 C、异面直线与所成的角为60° D、平面11. 已知直线与抛物线交于 , 两点,为坐标原点, , 交于点 , 点的坐标为 , 则的值为( )A、 B、2 C、 D、312. 已知函数定义域为 , 为偶函数,为奇函数,且满足 , 则( )A、 B、0 C、2 D、2023
A、该模型外接球的半径为 B、当时,的长度最小 C、异面直线与所成的角为60° D、平面11. 已知直线与抛物线交于 , 两点,为坐标原点, , 交于点 , 点的坐标为 , 则的值为( )A、 B、2 C、 D、312. 已知函数定义域为 , 为偶函数,为奇函数,且满足 , 则( )A、 B、0 C、2 D、2023二、填空题
-
13. 的展开式中的项系数为;14. 已知四边形是边长为2的正方形,若 , 且为的中点,则 .15. 经过点以及圆与交点的圆的方程为 .16. 已知函数 , 若有两个不同的极值点 , 且 , 则的取值范围为 .
三、解答题
-
17. 已知数列满足 .(1)、求数列的通项公式;(2)、若 , 求数列前项和 .18. 如图,正四棱锥的底面边长和高均为2, , 分别为 , 的中点.
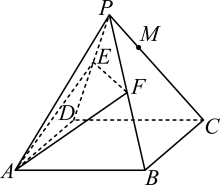 (1)、若点是线段上的点,且 , 判断点是否在平面内,并证明你的结论;(2)、求直线与平面所成角的正弦值.19. 世界杯足球赛淘汰赛阶段的比赛规则为:90分钟内进球多的球队取胜,如果参赛双方在90分钟内无法决出胜负(踢成平局),将进行30分钟的加时赛,若加时赛阶段两队仍未分出胜负,则进入“点球大战”.点球大战的规则如下:①两队各派5名队员,双方轮流踢点球,累计进球个数多者胜;②如果在踢满5球前,一队进球数已多于另一队踢5球可能踢中的球数,则该队胜出,譬如:第4轮结束时,双方进球数比 , 则不需踢第5轮了;③若前5轮点球大战中双方进球数持平,则采用“突然死亡法”决出胜负,即从第6轮起,双方每轮各派1人踢点球,若均进球或均不进球,则继续下一轮.直到出现一方进球另一方不进球的情况,进球方胜.现有甲乙两队在淘汰赛中相遇,双方势均力敌,120分钟(含加时赛)仍未分出胜负,须采用“点球大战”决定胜负.设甲队每名球员射进的概率为 , 乙队每名球员射进的概率为 . 每轮点球结果互不影响.(1)、设甲队踢了5球,为射进点球的个数,求的分布列与期望;(2)、若每轮点球都由甲队先踢,求在第四轮点球结束时,乙队进了4个球并刚好胜出的概率.20. 已知椭圆:的离心率为 , 且过点 .(1)、求椭圆的方程;(2)、设不过点的直线与椭圆交于 , 两点,关于原点的对称点为 , 记直线 , , 的斜率分别为 , , , 若 , 证明直线的斜率为定值.
(1)、若点是线段上的点,且 , 判断点是否在平面内,并证明你的结论;(2)、求直线与平面所成角的正弦值.19. 世界杯足球赛淘汰赛阶段的比赛规则为:90分钟内进球多的球队取胜,如果参赛双方在90分钟内无法决出胜负(踢成平局),将进行30分钟的加时赛,若加时赛阶段两队仍未分出胜负,则进入“点球大战”.点球大战的规则如下:①两队各派5名队员,双方轮流踢点球,累计进球个数多者胜;②如果在踢满5球前,一队进球数已多于另一队踢5球可能踢中的球数,则该队胜出,譬如:第4轮结束时,双方进球数比 , 则不需踢第5轮了;③若前5轮点球大战中双方进球数持平,则采用“突然死亡法”决出胜负,即从第6轮起,双方每轮各派1人踢点球,若均进球或均不进球,则继续下一轮.直到出现一方进球另一方不进球的情况,进球方胜.现有甲乙两队在淘汰赛中相遇,双方势均力敌,120分钟(含加时赛)仍未分出胜负,须采用“点球大战”决定胜负.设甲队每名球员射进的概率为 , 乙队每名球员射进的概率为 . 每轮点球结果互不影响.(1)、设甲队踢了5球,为射进点球的个数,求的分布列与期望;(2)、若每轮点球都由甲队先踢,求在第四轮点球结束时,乙队进了4个球并刚好胜出的概率.20. 已知椭圆:的离心率为 , 且过点 .(1)、求椭圆的方程;(2)、设不过点的直线与椭圆交于 , 两点,关于原点的对称点为 , 记直线 , , 的斜率分别为 , , , 若 , 证明直线的斜率为定值.