河南省普高联考2022-2023学年高三下学期理数测评试卷(四)
试卷更新日期:2023-03-10 类型:高考模拟
一、单选题
-
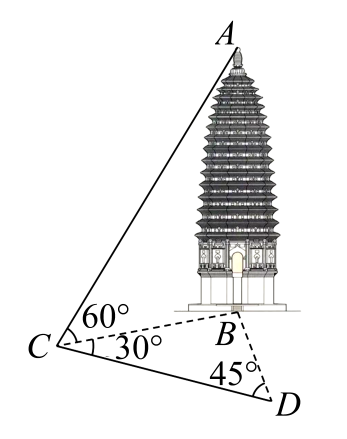
1. 已知集合 , , 则( )A、 B、 C、 D、2. 若复数z的共轭复数为 , 且 , 则z的虚部为( )A、 B、 C、 D、23. 已知等比数列的前n项和为 , 且 , , 则( )A、 B、5 C、 D、4. 塔是一种在亚洲常见的,有着特定的形式和风格的中国传统建筑.最初是供奉或收藏佛骨、佛像、佛经、僧人遗体等的高耸型点式建筑,称“佛塔”.如图,为测量某塔的总高度AB,选取与塔底B在同一水平面内的两个测量基点C与D,现测得 , , 米,在C点测得塔顶A的仰角为60°,则塔的总高度约为( )(参考数据: , )
 A、13米 B、24米 C、39米 D、45米5. 函数的大致图象是( )A、
A、13米 B、24米 C、39米 D、45米5. 函数的大致图象是( )A、 B、
B、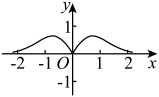 C、
C、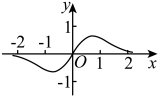 D、
D、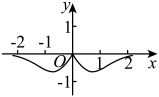 6. 某学校为落实“双减”政策,在课后服务时间开展了“绘画、书法、围棋、舞蹈、武术”五项兴趣拓展活动,小明计划从这五项活动中选择三项,则书法、舞蹈这两项活动至多有一项被选中的概率为( )A、0.9 B、0.7 C、0.6 D、0.37. 记不等式组的解集为D,现有下面四个命题:
6. 某学校为落实“双减”政策,在课后服务时间开展了“绘画、书法、围棋、舞蹈、武术”五项兴趣拓展活动,小明计划从这五项活动中选择三项,则书法、舞蹈这两项活动至多有一项被选中的概率为( )A、0.9 B、0.7 C、0.6 D、0.37. 记不等式组的解集为D,现有下面四个命题:, ; , ;
, ; , .
其中真命题的个数是( )
A、1 B、2 C、3 D、48. 已知抛物线的焦点为F,过点F的直线与抛物线交于点A,B,与抛物线的准线交于点M,且点A位于第一象限,F恰好为AM的中点, , 则( )A、 B、 C、 D、9. 任意写出一个正整数 , 并且按照以下的规律进行变换:如果是个奇数,则下一步变成 , 如果是个偶数,则下一步变成 , 无论是怎样一个数字,最终必进入循环圈 , 这就是数学史上著名的“冰雹猜想”.它可以表示为数列(为正整数), , 若 , 则的所有可能取值之和为( )A、188 B、190 C、192 D、20110. 在菱形ABCD中, , , AC与BD的交点为G,点M,N分别在线段AD,CD上,且 , , 将沿MN折叠到 , 使 , 则三棱锥的外接球的表面积为( )A、 B、 C、 D、11. 设双曲线的左、右焦点分别为 , , B为双曲线E上在第一象限内的点,线段与双曲线E相交于另一点A,AB的中点为M,且 , 若 , 则双曲线E的离心率为( )A、 B、2 C、 D、12. 已知 , , , 其中e为自然对数的底数,则( )A、 B、 C、 D、二、填空题
-
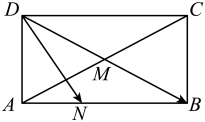
13. 二项式的展开式中的系数为 .14. 如图,在矩形ABCD中, , AC与BD的交点为M,N为边AB上任意点(包含端点),则的最大值为 .
 15. 圆与x轴交于A,B两点(A在B的左侧),点N满足 , 直线与圆M和点N的轨迹同时相切,则直线l的斜率为 .16. 先将函数的图象向左平移个单位长度,再将所得图象上所有点的横坐标变为原来的 , 纵坐标不变,所得图象与函数的图象关于x轴对称,若函数在上恰有两个零点,且在上单调递增,则的取值范围是 .
15. 圆与x轴交于A,B两点(A在B的左侧),点N满足 , 直线与圆M和点N的轨迹同时相切,则直线l的斜率为 .16. 先将函数的图象向左平移个单位长度,再将所得图象上所有点的横坐标变为原来的 , 纵坐标不变,所得图象与函数的图象关于x轴对称,若函数在上恰有两个零点,且在上单调递增,则的取值范围是 .三、解答题
-
17. 在中,角A,B,C的对边分别为a,b,c,且 .(1)、求A;(2)、若的面积为 , 点D在线段AC上,且 , 求BD的最小值.18. 如图,在四棱锥中,底面ABCD是平行四边形, , , , , 点M在底面ABCD上的射影为CD的中点O,E为线段AD上的点(含端点).
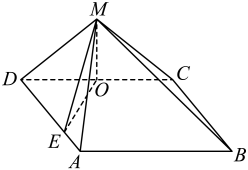 (1)、若E为线段AD的中点,证明:平面平面MAD;(2)、若 , 求二面角的余弦值.19. 某公司为了解年营销费用x(单位:万元)对年销售量y(单位:万件)的影响,统计了近5年的年营销费用和年销售量 , 得到的散点图如图所示,对数据进行初步处理后,得到一些统计量的值如下表所示.
(1)、若E为线段AD的中点,证明:平面平面MAD;(2)、若 , 求二面角的余弦值.19. 某公司为了解年营销费用x(单位:万元)对年销售量y(单位:万件)的影响,统计了近5年的年营销费用和年销售量 , 得到的散点图如图所示,对数据进行初步处理后,得到一些统计量的值如下表所示.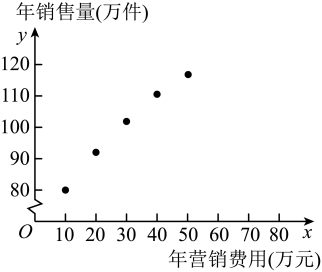
表中 , , , . 已知可以作为年销售量y关于年营销费用x的回归方程.
参考数据: , .
参考公式:对于一组数据 , 其回归直线的斜率和截距的最小二乘估计分别为 , .
(1)、求y关于x的回归方程;(2)、若公司每件产品的销售利润为4元,固定成本为每年120万元,用所求的回归方程估计该公司每年投入多少营销费用,才能使得该产品一年的收益达到最大?(收益销售利润营销费用固定成本)20. 已知椭圆的右焦点为F,离心率为 , 且点在㮋圆上.(1)、求椭圆C的标准方程;(2)、过右焦点F且斜率不为0的直线l与椭圆C交于A,B两点,线段AB的中点为Q,经过坐标原点O和点Q的直线m与椭圆C交于M,N两点,求四边形AMBN的面积的取值范围.