云南省昆明市2023年中考数学第一次模拟试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

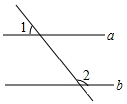
1. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4600000000人，这个数用科学记数法表示为（）．

A、 $46 \times 1 0^{8}$ B、 $4.6 \times 1 0^{8}$ C、 $4.6 \times 1 0^{9}$ D、 $4.6 \times 1 0^{10}$

查看试题解析
2. 当前，手机移动支付已经成为新型的消费方式，中国正在向无现金发展．元旦当天小明妈妈收到微信红包80元记作+80元，则小明妈妈微信转账支付65元记作（）

A、+80元 B、-80元 C、+65元 D、-65元

查看试题解析
3. 如图，直线 $a ∥ b$ ，若∠1＝52°，则∠2的度数为（）

A、152° B、138° C、128° D、142°

查看试题解析
4. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $M (- 2 ， - 3)$ ，则该函数的图象位于（）

A、第一、三象限 B、第二、三象限 C、第二、四象限 D、第三、四象限

查看试题解析
5. 如图，在△ABC中两条中线BE、CD相交于点O，记△DOE的面积为S₁ ， △COB的面积为S₂ ，则S₁：S₂＝（）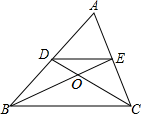

A、1：4 B、2：3 C、1：3 D、1：2

查看试题解析
6. 2022年2月22日春城飘雪，低温挡不住昆明人对雪的热情.21日至27日一周昆明每天的最低气温（单位：℃）分别为：2，-1，1，3，5，5，6，则下列关于这组数据说法错误的是（）．

A、平均数是3 B、方差是 $\frac{23}{7}$ C、中位数是3 D、众数是5

查看试题解析
7. 如图是几何体的三视图，该几何体是（）

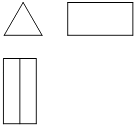A、圆锥 B、圆柱 C、正三棱柱 D、正三棱锥

查看试题解析
8. 探索规律：观察下面的一列单项式： $x$ 、 $- 2 x^{2}$ 、 $4 x^{3}$ 、 $- 8 x^{4}$ 、 $16 x^{5}$ 、…，根据其中的规律得出的第9个单项式是（）

A、 $- 256 x^{9}$ B、 $256 x^{9}$ C、 $- 512 x^{9}$ D、 $512 x^{9}$

查看试题解析
9. 下列说法正确的是（）

A、平分弦的直径垂直于弦，并且平分弦所对的两条弧； B、圆的切线垂直于圆的半径； C、三角形的外心到三角形三边的距离相等； D、同弧或等弧所对的圆周角相等；

查看试题解析
10. 下列运算正确的是（）

A、 $| - (- 2) | = 2$ B、 $3 + \sqrt{3} = 3 \sqrt{3}$ C、 ${(\frac{1}{2})}^{- 1} = - 2$ D、 ${(a b^{3})}^{2} = a b^{6}$

查看试题解析
11. 如图，已知 $∠ D A B = ∠ C A B$ ，添加下列条件不能判定 $△ D A B ≌ △ C A B$ 的是（）

A、 $∠ D B E = ∠ C B E$ B、 $∠ D = ∠ C$ C、 $D A = C A$ D、 $D B = C B$

查看试题解析
12. 随着市场对新冠疫苗需求越来越大，为满足市场需求，某大型疫苗生产企业更新技术后，加快了生产速度，现在平均每天比更新技术前多生产10万份疫苗，现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间相同，设更新技术前每天生产x万份，依据题意得（）

A、 $\frac{400}{x - 10} = \frac{500}{x}$ B、 $\frac{400}{x} = \frac{500}{x + 10}$ C、 $\frac{400}{x} = \frac{500}{x - 10}$ D、 $\frac{400}{x + 10} = \frac{500}{x}$

查看试题解析

二、填空题

13. 要使式子 $\frac{\sqrt{x - 5}}{3}$ 有意义，x的取值范围是．

查看试题解析
14. 在平面直角坐标系中，已知点 $A (a ， - 3)$ 与点 $B (2 ， b)$ 关于原点对称，则ab= ．

查看试题解析
15. 因式分解： $x^{2} - 4 =$ .

查看试题解析
16. 已知 $(x^{2} + y^{2} - 1) (x^{2} + y^{2} + 2) = 0$ ，则 $x^{2} + y^{2}$ 的值为．

查看试题解析
17. 某中学开展劳动实习，学生到教具加工厂制作圆锥，他们制作的圆锥，母线长为30cm，底面圆的半径为10 cm，这种圆锥的侧面展开图的圆心角度数是．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A C = 4$ ， $∠ A = 60 °$ ， $∠ B = 45 °$ ， $B C$ 边的垂直平分线 $D E$ 交 $A B$ 于点 $D$ ，连接 $C D$ ，则 $A B$ 的长为．

查看试题解析

三、解答题

19. 学了《数据的收集与表示》后，小刚就本班同学的上学方式进行了一次调查统计，左图和右图是他通过采集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息，解答以下问题：

(1)、求该班共有多少名学生？

(2)、在图中，将表示“步行”的部分补充完整；

(3)、在扇形统计图中，计算出“骑车”部分所对应的圆心角的度数；

(4)、如果全年级共500名同学，请你估算全年级步行上学的学生人数．

查看试题解析
20. 在不透明的袋子里装有2个红球和1个蓝球，红球和蓝球除颜色外其余都完全相同．

(1)、从袋子中一次摸出两个球，请用画树状图或列表的方法，求摸出的两个球是一红一蓝的概率；

(2)、若再向袋中放入若干个同样的蓝球，搅拌均匀后，使从袋中摸出一个蓝球的概率为 $\frac{3}{4}$ ，求后来放入袋中蓝球的个数．

查看试题解析
21. 如图， $△ A B C$ 中， $∠ A B C = ∠ A C B$ ， $E$ 在线段 $A C$ 上， $D$ 在 $A B$ 的延长线上，连 $D E$ 交 $E C$ 于 $F$ ，过 $E$ 作 $E G ⊥ B C$ 于 $G$ ．

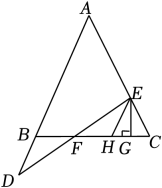(1)、若 $∠ A = 40 °$ ， $∠ D = 25 °$ ，试判断 $△ E F G$ 的形状；并说明理由．

(2)、若 $E H / / A D$ ， $B D = C E$ ，求证： $F G = B F + C G$ ．

查看试题解析
22. 某地区为打造乡村振兴示范区．实行大面积机械化种植，今年共计种植某作物700亩，预计租用10台作物收割机在一天之内完成该作物的收割。已知可租用A、B两种型号的作物收割机，2台A型号收割机与3台B型号收割机一起工作1天共收制该作物310亩，1台A型号收割机和1台B型号收割机一起工作1天共收割该作物130亩，租用A型号收割机的租金为每天3000元，租用B型号收割机的租金为每天2000元．

(1)、两种型号收割机每台每天平均收割多少亩该作物?

(2)、设租用x台A型号的收割机，完成该作物的收割需要的总租金为y元，一共有多少种租赁方案，并求出最少的总租金．

查看试题解析
23. 已知四边形 $A B C D$ 是正方形．

(1)、如图1所示，点O是正方形对角线的交点，连接 $O B$ ， $O C$ ，若 $A B = 4$ ，求 $O B$ 的长．

(2)、如图2所示，当点O是 $B C$ 上一点， $O C^{'} ⊥ B C$ ，连接 $B C^{'}$ ， $C^{'} D$ ，点M是 $C^{'} D$ 的中点，连接 $O M$ ， $C M$ ，求证： $C M = O M$ ．

查看试题解析
24. 抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 交x轴于A、B两点，交y轴正半轴于点C，对称轴为直线 $x = - \frac{3}{2}$ ．

(1)、如图1，若点C坐标为 $(0 ， 2)$ ，则b= ， c=；

(2)、若点P为第二象限抛物线上一动点，在（1）的条件下，求四边形 $A B C P$ 面积最大时，点P坐标和四边形 $A B C P$ 的最大面积；

(3)、如图2，点D为抛物线的顶点，过点O作 $M N ∥ C D$ 别交抛物线于点M，N，当 $M N = 3 C D$ 时，求c的值．

查看试题解析