山东省泰安市岱岳区2023年中考模拟训练数学题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 下列实数中的无理数是( )A、0.7 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,直线被直线所截, , , 则的度数为( )
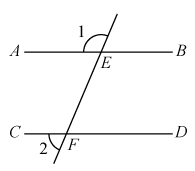 A、 B、 C、 D、4. 第24届冬季奥林匹克运动会于2022年2月4日在我国开幕,开幕后的第一周就累计吸引了约599000000名中国观众,将数据599000000用科学记数法表示应为 , 则n的值为( )A、7 B、8 C、9 D、105. 五名同学捐款数分别是5,3,6,5,10(单位:元),捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比,集中趋势相同的是()A、只有平均数 B、只有中位数 C、只有众数 D、中位数和众数6. 一个由长方体截去一部分后得到的几何体如图水平放置,其俯视图是( )
A、 B、 C、 D、4. 第24届冬季奥林匹克运动会于2022年2月4日在我国开幕,开幕后的第一周就累计吸引了约599000000名中国观众,将数据599000000用科学记数法表示应为 , 则n的值为( )A、7 B、8 C、9 D、105. 五名同学捐款数分别是5,3,6,5,10(单位:元),捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比,集中趋势相同的是()A、只有平均数 B、只有中位数 C、只有众数 D、中位数和众数6. 一个由长方体截去一部分后得到的几何体如图水平放置,其俯视图是( ) A、
A、 B、
B、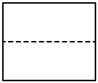 C、
C、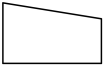 D、
D、 7. 如图, 内接于 ,CD是 的直径, ,则 ( )
7. 如图, 内接于 ,CD是 的直径, ,则 ( )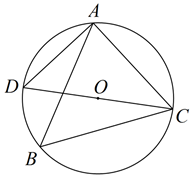 A、70° B、60° C、50° D、40°8. 中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有个,甜果有个,则可列方程组为( )A、 B、 C、 D、9. 如图,在中,以为直径的分别与交于点F,D,点F是的中点,连接交于点E.若 . 连接 , 则弦的长为( )
A、70° B、60° C、50° D、40°8. 中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有个,甜果有个,则可列方程组为( )A、 B、 C、 D、9. 如图,在中,以为直径的分别与交于点F,D,点F是的中点,连接交于点E.若 . 连接 , 则弦的长为( )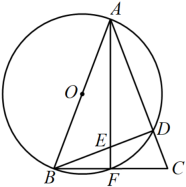 A、 B、 C、4 D、510. 如图,二次函数的图像与轴相交于 , 两点,对称轴是直线 , 下列说法正确的是( )
A、 B、 C、4 D、510. 如图,二次函数的图像与轴相交于 , 两点,对称轴是直线 , 下列说法正确的是( )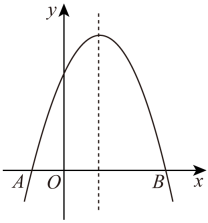 A、 B、当时,的值随值的增大而增大 C、点的坐标为 D、11. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:
A、 B、当时,的值随值的增大而增大 C、点的坐标为 D、11. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:①;②;③;④.其中正确结论的个数为( )
 A、1个 B、2个 C、3个 D、4个12. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )
A、1个 B、2个 C、3个 D、4个12. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )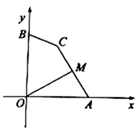 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知二元一次方程组 , 则的值为.14. 河堤横断面如图所示,堤高米,迎水坡的坡度是 , 则的长是米.
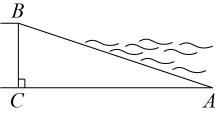 15. 如图,在长方形中,分别以点A,C为圆心, , 长为半径画弧,两弧均交对角线AC于点O.若 , 则图中阴影部分的面积为 . (结果不取近似值)
15. 如图,在长方形中,分别以点A,C为圆心, , 长为半径画弧,两弧均交对角线AC于点O.若 , 则图中阴影部分的面积为 . (结果不取近似值) 16. 如图,抛物线与x轴正半轴交于两点,y轴负半轴交于点C.若点 , 则下列结论中: ;;与是抛物线上两点,若 , 则;若抛物线的对称轴是直线 , m为任意实数,则;若则其中正确结论的个数共有个.
16. 如图,抛物线与x轴正半轴交于两点,y轴负半轴交于点C.若点 , 则下列结论中: ;;与是抛物线上两点,若 , 则;若抛物线的对称轴是直线 , m为任意实数,则;若则其中正确结论的个数共有个.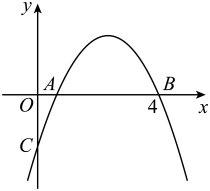 17. 如图,在矩形ABCD中,AB=1,AD= ,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为.
17. 如图,在矩形ABCD中,AB=1,AD= ,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为. 18. 如图,ΔABC是边长为1的等边三角形,分别取AC,BC边的中点D,E,连接DE,作得到四边形EDAF,它的周长记作C1;分别取EF,BE的中点D1 , E1连接D1E1 , 作 , 得到四边形E1D1FF1 , 它的周长记作C2 , 照此规律作下去,则C2021等于 .
18. 如图,ΔABC是边长为1的等边三角形,分别取AC,BC边的中点D,E,连接DE,作得到四边形EDAF,它的周长记作C1;分别取EF,BE的中点D1 , E1连接D1E1 , 作 , 得到四边形E1D1FF1 , 它的周长记作C2 , 照此规律作下去,则C2021等于 .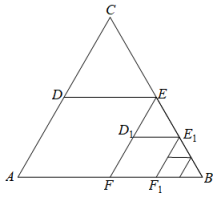
三、解答题
-
19. 先化简,再求值: ,其中 .20. 某学校为了解全校学生对电视节目(新闻、体育、动画、娱乐、戏曲)的喜爱情况,从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
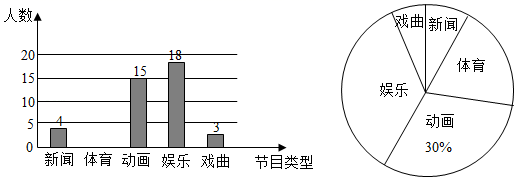
请根据以上信息,解答下列问题
(1)、这次被调查的学生共有多少名?(2)、请将条形统计图补充完整;(3)、若该校有3000名学生,估计全校学生中喜欢体育节目的约有多少名?(4)、该校宣传部需要宣传干事,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,用树状图或列表法求恰好选中甲、乙两位同学的概率.21. 端午节吃粽子是中华民族的传统习俗.某超市节前购进了甲、乙两种畅销口味的粽子.已知购进甲种粽子的金额是1200元,购进乙种粽子的金额是800元,购进甲种粽子的数量比乙种粽子的数量少50个,甲种粽子的单价是乙种粽子单价的2倍.(1)、求甲、乙两种粽子的单价分别是多少元?(2)、为满足消费者需求,该超市准备再次购进甲、乙两种粽子共200个,若总金额不超过1150元,问最多购进多少个甲种粽子?22. 如图,一次函数 与反比例函数 交于 、 两点,其中点 的坐标为 .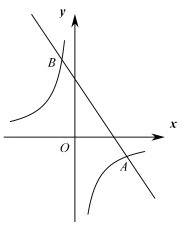 (1)、求一次函数与反比例函数的解析式;(2)、在第二象限的反比例函数图象上是否存在一点 ,使得 的面积是 面积的2倍?若存在,求出点 的横坐标,若不存在,请说明理由;(3)、请结合图形,直接写出不等式 的解集.23. 如图,在Rt△ABC中, , AC=BC,D为斜边AB上一动点(不与端点A,B重合),以C为旋转中心,将CD逆时针旋转90°得到CE,连接AE,BE,F为AE的中点.
(1)、求一次函数与反比例函数的解析式;(2)、在第二象限的反比例函数图象上是否存在一点 ,使得 的面积是 面积的2倍?若存在,求出点 的横坐标,若不存在,请说明理由;(3)、请结合图形,直接写出不等式 的解集.23. 如图,在Rt△ABC中, , AC=BC,D为斜边AB上一动点(不与端点A,B重合),以C为旋转中心,将CD逆时针旋转90°得到CE,连接AE,BE,F为AE的中点.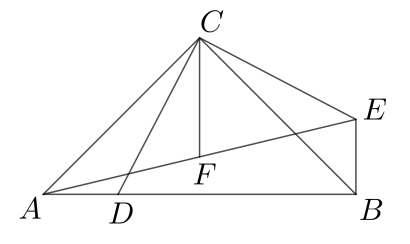 (1)、求证:;(2)、用等式表示线段CD,BE,CF三者之间数量关系,并说明理由;(3)、若CF= , CD= , 求的值.24. 如图,抛物线经过 , 两点,与x轴交于另一点A,点D是抛物线的顶点.
(1)、求证:;(2)、用等式表示线段CD,BE,CF三者之间数量关系,并说明理由;(3)、若CF= , CD= , 求的值.24. 如图,抛物线经过 , 两点,与x轴交于另一点A,点D是抛物线的顶点.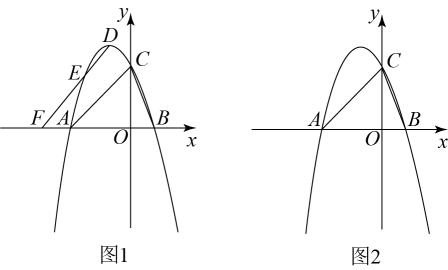 (1)、求抛物线的解析式及点D的坐标;(2)、如图1,点E在抛物线上,连接并延长交x轴于点F,连接 , 若是以为底的等腰三角形,求点E坐标.(3)、如图2,连接、 , 在抛物线上是否存在点M,使 , 若存在,求出M点的坐标;若不存在,请说明理由.25. 感知:数学课上,老师给出了一个模型:如图1,点A在直线上,且 , 像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角“模型.
(1)、求抛物线的解析式及点D的坐标;(2)、如图1,点E在抛物线上,连接并延长交x轴于点F,连接 , 若是以为底的等腰三角形,求点E坐标.(3)、如图2,连接、 , 在抛物线上是否存在点M,使 , 若存在,求出M点的坐标;若不存在,请说明理由.25. 感知:数学课上,老师给出了一个模型:如图1,点A在直线上,且 , 像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角“模型.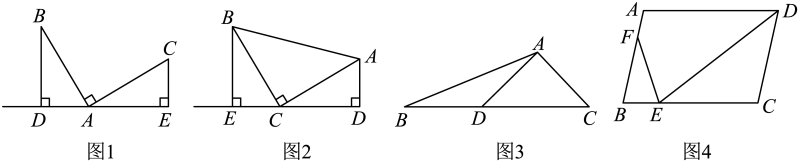
应用:
(1)、如图2,中, , 直线经过点C,过A作于点D,过B作于点E.求证: .(2)、如图3,在中,D是上一点,, 求点C到边的距离.
(3)、如图4,在中,E为边上的一点,F为边上的一点.若 , 求 的值.