山东省青岛市2023年中考数学一模试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 绝对值为 $\frac{1}{5}$ 的数是（）

A、5 B、 $\frac{1}{5}$ C、 $- \frac{1}{5}$ D、 $\pm \frac{1}{5}$

查看试题解析
2. Iphone15系列苹果手机预计于2023年9月份上市中国大陆．其内部的A16芯片加入光线追踪功能，将宽度压缩到0.000000005米．将数字0.000000005米用科学记数法表示为（）

A、 $- 5 \times 1 0^{9}$ 米 B、 $- 0.5 \times 1 0^{8}$ 米 C、 $0.5 \times 1 0^{- 8}$ 米 D、 $5 \times 1 0^{- 9}$ 米

查看试题解析
3. 中秋节上，同学设计了如图的艺术字“中秋快乐”，下面展示如图几何体“中”字的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 如图， $B C$ 是 $⊙ O$ 的直径，点A是 $⊙ O$ 外一点，连接 $A C$ 交 $⊙ O$ 于点 $E$ ，连接 $A B$ 并延长交 $⊙ O$ 于点 $D$ ．若 $∠ A = 35 °$ ，则 $∠ D O E$ 的度数是（）

A、 $110 °$ B、 $120 °$ C、 $120.5 °$ D、 $115 °$

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ A B C + ∠ A C B = α$ ，按图进行翻折，使 $M D ∥ N G ∥ B C$ ， $M E ∥ F G$ ，则 $∠ N F E$ 的度数是（）

A、 $2 α - 180 °$ B、 $180 ° - 2 α$ C、 $90 ° - α$ D、 $α - 90 °$

查看试题解析
6. 如图，在平面直角坐标系中，△ABC位于第二象限，点A的坐标是 $(- 2 ， 3)$ ，先将△ABC绕点 $(- 1 ， 0)$ 顺时针旋转90度得到 $△ A_{1} B_{1} C_{1}$ ，再以原点为位似中心作 $△ A_{1} B_{1} C_{1}$ 的位似图形 $△ A_{2} B_{2} C_{2}$ ，若 $△ A_{1} B_{1} C_{1}$ 与 $△ A_{2} B_{2} C_{2}$ 的相似比为1∶2，则点A的对应点 $A_{2}$ 的坐标是（）

A、 $(4 ， 2)$ B、 $(6 ， 4)$ C、 $(6 ， 4)$ 或 $(- 6 ， - 4)$ D、 $(4 ， 2)$ 或 $(- 4 ， - 2)$

查看试题解析
7. 如图，在正方形 $A B C D$ 中， $A B = 4$ ， $E$ 为 $B C$ 的中点，将 $△ A B E$ 沿 $A E$ 折叠，使点 $B$ 落在正方形内点 $F$ 处，连接 $C F$ ，则 $C F$ 的长为（）

A、 $2 \sqrt{2}$ B、 $\sqrt{19} - \sqrt{3}$ C、 $\frac{4 \sqrt{5}}{5}$ D、2.25

查看试题解析
8. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像的一部分如图所示，已知图像经过点 $(- 1 ， 0)$ ，其对称轴为直线 $x = 1$ ．下列结论：① $a b c < 0$ ；② $b^{2} - 4 a c < 0$ ；③ $8 a + c < 0$ ；④ $9 a + 3 b + 2 c < 0$ ；⑤点 $C (x_{1} ， y_{1}) D (x_{2} ， y_{2})$ 是抛物线上的两点，若 $x_{1} < x_{2}$ ，则 $y_{1} < y_{2}$ ；⑥若抛物线经过点 $(- 3 ， n)$ ，则关于 $x$ 的一元二次方程 $a x^{2} + b x + c - n = 0 (a \neq 0)$ 的两根分别为-3，5；其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

9. 计算： $\frac{\sqrt{12} \times \sqrt{2}}{\sqrt{3}} - 2 s i n 4 5^{°} =$

查看试题解析
10. 已知关于的 $x$ 方程 $(m - 1) x^{2} - \sqrt{2 - m} x - \frac{1}{2} = 0$ 有两个实数根，则 $m$ 的取值范围是．

查看试题解析
11. 已知甲、乙两队员射击的成绩如图，设甲、乙两队员射击成绩的方差分别为 $s_{甲}^{2}$ 、 $s_{乙}^{2}$ ，则 $s_{甲}^{2}$ $s_{乙}^{2}$ ．（填“ $>$ ”、“ $=$ ”、“ $<$ ”）

查看试题解析
12. 某产品每件的生产成本为50元，原定销售价65元，经市场预测，从现在开始的第一季度销售价格将下降10%，第二季度又将回升5%．若要使半年以后的销售利润不变，设每个季度平均降低成本的百分率为x ，根据题意可列方程是．

查看试题解析
13. 如图所示，ABCD为矩形，以CD为直径作半圆，矩形的另外三边分别与半圆相切，沿着折痕DF折叠该矩形，使得点C的对应点E落在AB边上，若AD＝2，则图中阴影部分的面积为．

查看试题解析
14. 如图，正方形 $A B C D$ 的边长为6，点 $E ， F$ 分别为边 $B C$ ， $C D$ 上两点 $C F = B E$ ， $A E$ 平分 $∠ B A C$ ，连接 $B F$ ，分别交 $A E ， A C$ 于点 $G ， M$ ，点 $P$ 是线段 $A G$ 上的一个动点，过点 $P$ 作 $P N ⊥ A C$ ，垂足为 $N$ ，连接 $P M$ ，下列说法：① $Δ A B E ≅ Δ B C F$ ；② $A M = 4 \sqrt{2}$ ；③ $S_{△ A G M} = \frac{9}{2} \sqrt{2}$ ；④ $P M + P N$ 的最小值为 $3 \sqrt{2}$ ；正确的是．（填序号）

查看试题解析

三、解答题

15. 已知： $△ A B C$ ．求作： $△ A B C$ 的外接圆内的点P，使 $∠ P = 2 ∠ A$ ， $P B = P C$ ．请用直尺、圆规作图，不写作法，但要保留作图痕迹．

查看试题解析
16.

(1)、计算： $\frac{2 x + 4}{x^{2} - 6 x + 9} \div (\frac{2 x - 1}{x - 3} - 1)$ ；

(2)、解不等式组 ${\begin{array}{l} 5 x - 2 > 3 (x + 1) \\ \frac{1}{2} x - 1 \geq 7 - \frac{3}{2} x \end{array}$ ．

查看试题解析
17. 有四张反面完全相同的纸牌 $A ， B ， C ， D$ ，其正面分别画有四个不同的几何图形，将四张纸牌洗匀正面朝下随机放在桌面上．

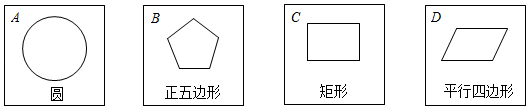(1)、从四张纸牌中随机摸出一张，摸出的牌面图形是中心对称图形的概率是．

(2)、小明和小亮约定做一个游戏，其规则为：先由小明随机摸出一张，不放回．再由小亮从剩下的纸牌中随机摸出一张，若摸出的两张牌面图形既是轴对称图形又是中心对称图形，则小亮获胜，否则小明获胜．这个游戏公平吗？请用列表法（或画树状图）说明理由．（纸牌用 $A ， B ， C ， D$ 表示）若不公平，请你帮忙修改一下游戏规则，使游戏公平．

查看试题解析
18. 为迎接新冠疫情的第一次高峰，青岛市市南区举行了线上期末考试，其评分等级如下：90分及以上为优秀；80分-89分为良好；60分-79分为及格；60分以下为不及格．教研员随机抽取学生的成绩进行分析，并将测试成绩制成如图表，据此回答下列问题：

(1)、扇形统计图中，“不及格”等级所在扇形圆心角的度数为°

(2)、求参加本次测试学生的平均成绩；

(3)、所抽取的这些学生测试成绩的中位数是落在等级；

(4)、根据实际情况，在线上学习期间认真的同学成绩应该达到良好及以上，若其中共有960人，请你估计，“不及格”有多少人．

查看试题解析
19. 如图，斜坡AB的坡角为33°，BC⊥AC，现计划在斜坡AB中点D处挖去部分坡体，用于修建一个平行于水平线CA且长为12m的平台DE和一条坡角为45°的新的陡坡BE．建筑物GH距离A处36米远（即AG为36米），小明在D处测得建筑物顶部H的仰角为36°．图中各点均在同一个平面内，且点C、A、G在同一条直线上，HG⊥CG，求建筑物GH的高度．（结果精确到1m）
（参考数据：sin33° $\approx \frac{11}{20}$ ， cos33° $\approx \frac{21}{20}$ ， tan33° $\approx \frac{3}{5}$ ， sin36° $\approx \frac{3}{5}$ ， cos36° $\approx \frac{4}{5}$ ， tan36° $\approx \frac{7}{10}$ ）

查看试题解析
20. 如图

【问题提出】

正多边形内任意一点到各边距离之和与这个正多边形的半径 $R$ 和中心角有什么关系？

【问题探究】

如图①， $△ A B C$ 是等边三角形，半径 $O A = R$ ， $∠ A O B$ 是中心角， $P$ 是 $△ A B C$ 内任意一点， $P$ 到 $△ A B C$ 各边距离 $P F$ 、 $P E$ 、 $P D$ 分别为 $h_{1} 、 h_{2} 、 h_{3}$ ，设 $△ A B C$ 的边长是 $a$ ，面积为 $S$ ．过点 $O$ 作 $O M ⊥ A B$ ．

∴ $O M = R c o s \frac{1}{2} ∠ A O B = R c o s 60 °$ ， $A M = R s i n \frac{1}{2} ∠ A O B = R s i n 60 °$ ， $A B = 2 A M = 2 R s i n 60 °$ ，

∴ $S_{△ A B C} = 3 S_{△ A O B} = 3 \times \frac{1}{2} A B \times O M = 3 R^{2} s i n 60 ° c o s 60 °$ ， ①

∵ $S_{△ A B C}$ 又可以表示 $\frac{1}{2} a (h_{1} + h_{2} + h_{3})$ ②

联立①②得 $\frac{1}{2} a (h_{1} + h_{2} + h_{3}) = 3 R^{2} s i n 60 ° c o s 60 °$

∴ $\frac{1}{2} \times 2 R s i n 60 ° (h_{1} + h_{2} + h_{3}) = 3 R^{2} s i n 60 ° c o s 60 °$

∴ $h_{1} + h_{2} + h_{3} = 3 R c o s 60 °$

(1)、【问题解决】
如图②，五边形 $A B C D E$ 是正五边形，半径 $O A = R$ ， $∠ A O B$ 是中心角， $P$ 是五边形 $A B C D E$ 内任意一点， $P$ 到五边形 $A B C D E$ 各边距 $P H 、 P M 、 P N 、 P I 、 P L$ 分别为 $h_{1}$ 、 $h_{2}$ 、 $h_{3}$ 、 $h_{4}$ 、 $h_{5}$ ，参照（1）的分析过程，探究 $h_{1} + h_{2} + h_{3} + h_{4} + h_{5}$ 的值与正五边形 $A B C D E$ 的半径 $R$ 及中心角的关系．

(2)、【性质应用】
正六边形（半径是 $R$ ）内任意一点 $P$ 到各边距离之和 $h_{1} + h_{2} + h_{3} + h_{4} + h_{5} + h_{6} =$ ．

(3)、如图③，正 $n$ 边形（半径是 $R$ ）内任意一点 $P$ 到各边距离之和 $h_{1} + h_{2} + ⋯ + h_{n - 1} + h_{n} =$ ．

查看试题解析
21. 小李从A地出发去相距4.5千米的B地上班，他每天出发的时间都相同．第一天步行去上班结果迟到了5分钟．第二天骑自行车去上班结果早到10分钟．已知骑自行车的速度是步行速度的1.5倍．

(1)、求小李步行的速度和骑自行车的速度；

(2)、有一天小李骑自行车出发，出发1.5千米后自行车发生故障．小李立即跑步去上班（耽误时间忽略不计）为了至少提前3分钟到达．则跑步的速度至少为多少千米每小时？

查看试题解析
22. 如图，直线 $y = k x + 3$ 与 $x$ 轴、 $y$ 轴分别交于点 $B 、 C$ ，与反比例函数 $y = \frac{m}{x}$ 交于点 $A 、 D$ ．过 $D$ 作 $D E ⊥ x$ 轴于 $E$ ，连接 $O A ， O D$ ，若 $A (- 2 ， n)$ ， $S_{Δ O A B} ： S_{Δ O D E} = 1 ： 2$

(1)、求反比例函数的表达式；

(2)、求点 $C$ 的坐标；

(3)、直接写出关于 $x$ 不等式： $\frac{m}{x} > k x - 3$ 的解集为．

查看试题解析
23. 已知：如图，正方形 $A B C D$ 的对角线相交于点O， $∠ C A B$ 的平分线分别交 $B D$ ， $B C$ 于点E，F，作 $B H ⊥ A F$ 于点H，分别交 $A C$ ， $C D$ 于点G，P，连接 $G E$ ， $G F$ ．

(1)、求证： $△ O A E ≌ △ O B G$ ；

(2)、判断四边形 $B F G E$ 是什么特殊四边形？并证明你的结论．

查看试题解析
24. 2022年2月，北京冬奥会成功举办，吉祥物纪念品等深受人们喜爱.某商店在冬奥会前购进数量相同的甲、乙两种纪念品，分别花费10400元，14000元，已知乙种纪念品比甲种纪念品每个进价多9元.

(1)、求甲、乙两种纪念品每个的进价.

(2)、经销中发现，甲种纪念品每个售价46元时，每天可售40个，乙种纪念品每个售价45元时，每天可售80个，商店决定甲种纪念品降价，乙种纪念品提价.结果甲种纪念品单价降1元可多卖4个，乙种纪念品单价提1元就少卖2个，若某天两种纪念品共销售140个，则这天最大利润是多少？

查看试题解析
25. 已知：如图，在四边形 $A B C D$ 中， $A B // C D$ ， $∠ A C B = 90 °$ ， $A B = 10 cm$ ， $B C = 8 cm$ ， $O D$ 垂直平分 $A$ $C$ .点 $P$ 从点 $B$ 出发，沿 $B A$ 方向匀速运动，速度为 $1 cm/s$ ；同时，点 $Q$ 从点 $D$ 出发，沿 $D C$ 方向匀速运动，速度为 $1 cm/s$ ；当一个点停止运动，另一个点也停止运动.过点 $P$ 作 $P E ⊥ A B$ ，交 $B C$ 于点 $E$ ，过点 $O$ 作 $Q F // A C$ ，分别交 $A D$ ， $O D$ 于点 $F$ ， $G$ .连接 $O P$ ， $E G$ .设运动时间为 $t (s)$ $(0 < t < 5)$ ，解答下列问题：

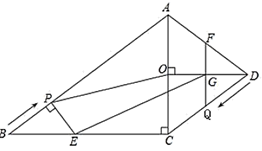(1)、当 $t$ 为何值时，点 $E$ 在 $∠ B A C$ 的平分线上？

(2)、设四边形 $P E G O$ 的面积为 $S (c m^{2})$ ，求 $S$ 与 $t$ 的函数关系式.

(3)、连接 $O E$ ， $O Q$ ，在运动过程中，是否存在某一时刻 $t$ ，使 $O E ⊥ O Q$ ？若存在，求出 $t$ 的值；若不存在，请说明理由.

查看试题解析