山东省青岛市市南区2023年一模数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 的相反数的倒数是( )A、 B、 C、 D、2. 中芯国际集成电路制造有限公司,是世界领先的集成电路晶圆代工企业之一,也是中国内地技术最先进、配套最完善、规模最大、跨国经营的集成电路制造企业集团,中芯国际第一代14纳米FinFET技术取得了突破性进展,并于2019年第四季度进入量产,代表了中国大陆自主研发集成电路的最先进水平,14纳米=0.000000014米,0.000000014用科学记数法表示为( )A、 B、 C、 D、3. 在一个密闭不透明的袋子里有若干个白球,为估计白球个数,丽丽向其中投入8个黑球,搅拌均匀后随机摸出一个球,记下颜色,再把它放入袋中,不断重复摸球100次,其中20次摸到黑球,则估计袋中大约有白球( )A、18个 B、28个 C、32个 D、42个4. 已知关于x的一元二次方程有两个不相等的实数根,则k的取值范围为( )A、 B、 C、且 D、且5. 如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(﹣2,3),先把△ABC向右平移4个单位长度得到△A1B1C1 , 再把△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1 , 则点A的对应点A2的坐标是( )
 A、(5,2) B、(1,0) C、(3,﹣1) D、(5,﹣2)6. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A、(5,2) B、(1,0) C、(3,﹣1) D、(5,﹣2)6. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) A、45° B、50° C、55° D、60°7. 如图,在矩形 中, ,在 上取一点 ,连接 、 ,将 沿 翻折,使点 落在 处,线段 交 于点 ,将 沿 翻折,使点 的对应点 落在线段 上,若点 恰好为 的中点,则线段 的长为( )
A、45° B、50° C、55° D、60°7. 如图,在矩形 中, ,在 上取一点 ,连接 、 ,将 沿 翻折,使点 落在 处,线段 交 于点 ,将 沿 翻折,使点 的对应点 落在线段 上,若点 恰好为 的中点,则线段 的长为( ) A、 B、 C、 D、8. 二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的图象大致为( )
A、 B、 C、 D、8. 二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 计算 .10. 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计,然后再按演讲内容占50%,演讲能力占40%、演讲效果占10%,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如表所示,则获得第一名的选手为 .
选手
演讲内容
演讲能力
演讲效果
小明
90
80
90
小红
80
90
90
11. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa) 是气体体积V(m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应 .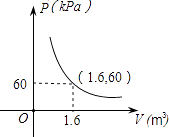 12. 某品牌瓶装饮料每箱价格是26元,某商店对该瓶装饮料进行“买一送三”的促销活动,即整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元,问该品牌饮料每瓶多少元?设该品牌饮料每瓶是x元,则可列方程为 .13. 如图,在平行四边形中, , 点E是中点.在上取一点F,以点F为圆心,的长为半径作圆,该圆与边恰好相切于点D,连接 , 则图中阴影部分面积为(结果保留).
12. 某品牌瓶装饮料每箱价格是26元,某商店对该瓶装饮料进行“买一送三”的促销活动,即整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元,问该品牌饮料每瓶多少元?设该品牌饮料每瓶是x元,则可列方程为 .13. 如图,在平行四边形中, , 点E是中点.在上取一点F,以点F为圆心,的长为半径作圆,该圆与边恰好相切于点D,连接 , 则图中阴影部分面积为(结果保留).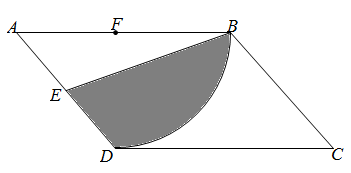 14. 如图,在矩形中,点是线段上的一点, , 将沿翻折,得到 , 若 , , 则点到的距离为 .
14. 如图,在矩形中,点是线段上的一点, , 将沿翻折,得到 , 若 , , 则点到的距离为 .
三、解答题
-
15. 已知:线段a,c.
求作:△ABC,使BC=a,AB=c,∠C=90°
 16. 计算(1)、化简:;(2)、解不等式组 , 并写出不等式组的最小整数解.17. 如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为1时,甲获胜;数字之和为2时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.
16. 计算(1)、化简:;(2)、解不等式组 , 并写出不等式组的最小整数解.17. 如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为1时,甲获胜;数字之和为2时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止. (1)、用画树状图或列表法求乙获胜的概率;(2)、这个游戏规则对甲、乙双方公平吗?对谁有利?请判断并说明理由.18. 青岛胶东机场即将投入使用,为测量该机场东西两建筑物A、B的距离.如图,勘测无人机在点C处,测得建筑物A的俯角为50°,CA的距离为2千米,然后沿着平行于AB的方向飞行6.4千米到点D,测得建筑物B的俯角为37°,求该机场东西两建筑物AB的距离.(结果精确到0.1千米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
(1)、用画树状图或列表法求乙获胜的概率;(2)、这个游戏规则对甲、乙双方公平吗?对谁有利?请判断并说明理由.18. 青岛胶东机场即将投入使用,为测量该机场东西两建筑物A、B的距离.如图,勘测无人机在点C处,测得建筑物A的俯角为50°,CA的距离为2千米,然后沿着平行于AB的方向飞行6.4千米到点D,测得建筑物B的俯角为37°,求该机场东西两建筑物AB的距离.(结果精确到0.1千米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20) 19. 劳动教育是新时代对教育的新要求,是中国特色社会主义教育制度的重要内容,是全面发展教育体系的重要内容,是大、中、小学必须开展的教育活动,某中学为落实劳动教育,组织八年级学生进行了劳动知识技能竞赛,现随机抽取了部分同学的成绩(百分制),绘制了统计图表:
19. 劳动教育是新时代对教育的新要求,是中国特色社会主义教育制度的重要内容,是全面发展教育体系的重要内容,是大、中、小学必须开展的教育活动,某中学为落实劳动教育,组织八年级学生进行了劳动知识技能竞赛,现随机抽取了部分同学的成绩(百分制),绘制了统计图表:表一:
成绩x
x<60
60≤x<70
70≤x<80
80≤x<90
90≤x≤100
人数
1
2
a
8
4
表二:
统计量
平均数
中位数
众数
成绩
79.7
b
72

请根据以上信息回答下列问题:
(1)、若抽取的学生竞赛成绩处在80≤x<90这一组的数据如下:88,87,81,80,82,88,84,86.根据以上数据填空:a= , b= .(2)、在扇形统计图中,表示竞赛成绩为90≤x≤100这一组所对应扇形的圆心角度数为 .(3)、已知该校八年级共有学生700名.若将竞赛成绩不少于80分的学生评为“劳动达人”,请你估计该校八年级被评为“劳动达人”的学生人数 .20. 2020年腊月,某商家根据天气预报预测羽绒服将畅销,就用26400元采购了一批羽绒服,后来羽绒服供不应求.商家又用57600元购进了一批同样的羽绒服,第二次所购数量是第一次所购数量的2倍,第二次购进的单价比第一次购进的单价贵了10元.(1)、该商家第一次购进的羽绒服有多少件?(2)、若两次购进的羽绒服销售时标价都相同,最后剩下50件按6折优惠卖出,若两批羽绒服全部售完后利润率不低于25%(不考虑其他因素),则每件羽绒服的标价至少为多少元?21. 已知:如图,在矩形ABCD中,E是边BC上一点,过点E作对角线AC的平行线,交AB于F,交DA和DC的延长线于点G,H. (1)、求证:△AFG≌△CHE;(2)、若∠G=∠BAC,则四边形ABCD是什么特殊四边形?并证明你的结论.22. “拼多多”汽车某租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金(元)与每月租出的车辆数有如下关系:
(1)、求证:△AFG≌△CHE;(2)、若∠G=∠BAC,则四边形ABCD是什么特殊四边形?并证明你的结论.22. “拼多多”汽车某租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金(元)与每月租出的车辆数有如下关系:x(元)
3000
3200
3500
4000
y(辆)
100
96
90
80
(1)、观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求按照表格呈现的规律,每月租出的车辆数(辆)与每辆车的月租金(元)之间的关系式.(2)、已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含的代数式填表:租出的车辆数(辆)
未租出的车辆数(辆)
租出每辆车的月收益(元)
所有未租出的车辆每
月的维护费(元)
(3)、若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请说明理由.23. 提出:把1到2022这2022个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数;擦去一数),转圈擦下去,最后剩下的是哪个数?
探究一:
从简单情况入手:
如果只有1,2,很明显,留下1,擦去2,最后剩下1;
如果只有1,2,3,4,如图所示,第一圈留下1,3擦去2,4;第二圈留下1,擦去3,最后剩下1;
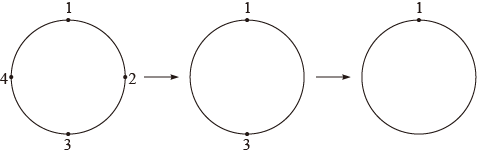
如果只有1,2,3,4,5,6,7,8,如图所示,第一圈留下1,3,5,7擦去2,4,6,8;第二圈留下1,5擦去3,7;第三圈留下1,擦去5;最后剩下1;

问题一:如果只有1,2,3,…,16这16个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4…(每隔一数,擦去一数),转圈擦下去,最后剩下的数是;
探究二:
如果只有1,2,3,4,5,6,7这7个数,由探究一可知只有4个数时,最后剩下的是1,即4个数中的“第一个数”,因此只要剩下4个数,即可知最后剩下的是哪个数.也就是先擦掉个数,擦掉的第3个数是6,它的下一个数是7,也就是剩下的4个数中的第一个是7,所以最后剩下的数就是7;
如果只有1,2,3,…,12这12个数,由探究一可知只有8个数时,最后剩下的是1,即8个数中的“第一个数”,因此只要剩下8个数,即可知最后剩下的是哪个数.也就是先擦掉个数,擦掉的第4个数是8,它的下一个数是9,也就是剩下的8个数中的第一个是9,所以最后剩下的数就是9;
仿照上面的探究方法,回答下列问题:
问题二,如果只有1,2,3,…,26这26个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,最后剩下的数是;
问题解决:
问题三:把1到2022这2022个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,最后剩下的数是;
一般归纳:
问题四:把1,2,3,…,n这个数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,如果 , 且n和k都是正整数,则最后剩下的数是;(用n、k的代数式表示)
拓展延伸:
问题五:如果只有1,2,3,…,n这n个数,且 , n是正整数,按顺时针方向依次排列在一个圆周上,从1开始按顺时针方向,保留1,擦去2,保留3,擦去4……(每隔一数,擦去一数),转圈擦下去,如果最后剩下的数是2023,则n可以为 .
24. 如图,在矩形中, , , 动点P从点D出发沿向终点A运动,同时动点Q从点A出发沿对角线向终点C运动.过点P作 , 交于点E,动点P、Q的运动速度是每秒1个单位长度,当点P运动到点A时,P、Q两点同时停止运动.设运动时间为 , 解答下列问题: (1)、当E、Q重合时,求t的值;(2)、设四边形的面积为S,当线段在点Q右侧时,求出S与t之间的函数关系式;(3)、当时,求t的值;(4)、是否存在这样的点P和点Q,使P、Q、E为顶点的三角形是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
(1)、当E、Q重合时,求t的值;(2)、设四边形的面积为S,当线段在点Q右侧时,求出S与t之间的函数关系式;(3)、当时,求t的值;(4)、是否存在这样的点P和点Q,使P、Q、E为顶点的三角形是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.