河北秦皇岛开发区20223九年级中考第一次模拟数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 如图,数轴上点A对应的数是 ,将点A沿数轴向左移动2个单位至点B,则点B对应的数是( )
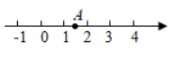 A、 B、-2 C、 D、2. 下列交通标志中,是中心对称图形的是( )A、
A、 B、-2 C、 D、2. 下列交通标志中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 根据图中三视图可知该几何体是( )
3. 根据图中三视图可知该几何体是( )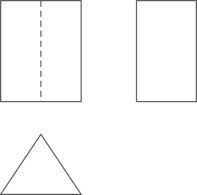 A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱4. 下列运算正确的是( )A、 B、 C、 D、5. 函数 的自变量x的取值范围是( )A、 ,且 B、 C、 D、 ,且6. 不等式组 的解集是( )A、 B、 C、 D、7. 在平面直角坐标系中,点G的坐标是 ,连接 ,将线段 绕原点O旋转 ,得到对应线段 ,则点 的坐标为( )A、 B、 C、 D、8. 如图,在中,D、E为边的三等分点, , H为与的交点.若 , 则( )
A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱4. 下列运算正确的是( )A、 B、 C、 D、5. 函数 的自变量x的取值范围是( )A、 ,且 B、 C、 D、 ,且6. 不等式组 的解集是( )A、 B、 C、 D、7. 在平面直角坐标系中,点G的坐标是 ,连接 ,将线段 绕原点O旋转 ,得到对应线段 ,则点 的坐标为( )A、 B、 C、 D、8. 如图,在中,D、E为边的三等分点, , H为与的交点.若 , 则( ) A、2 B、1 C、0.5 D、1.59. 如图,在 中, 为直径, ,点D为弦 的中点,点E为 上任意一点,则 的大小可能是( )
A、2 B、1 C、0.5 D、1.59. 如图,在 中, 为直径, ,点D为弦 的中点,点E为 上任意一点,则 的大小可能是( )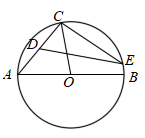 A、 B、 C、 D、10. 若二次函数 的图象,过不同的六点 、 、 、 、 、 ,则 、 、 的大小关系是( )A、 B、 C、 D、11. 化简的结果是( )A、 B、 C、 D、12. 不解方程,判别方程2x2-3x=3的根的情况( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无实数根13. 将抛物线向左平移1个单位长度,得到抛物线 , 则抛物线的解析式为( )A、 B、 C、 D、14. 如图,在中, , 将绕顶点C顺时针旋转得到 , D是的中点,连接BD,若 , , 则线段的最大值为( )
A、 B、 C、 D、10. 若二次函数 的图象,过不同的六点 、 、 、 、 、 ,则 、 、 的大小关系是( )A、 B、 C、 D、11. 化简的结果是( )A、 B、 C、 D、12. 不解方程,判别方程2x2-3x=3的根的情况( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无实数根13. 将抛物线向左平移1个单位长度,得到抛物线 , 则抛物线的解析式为( )A、 B、 C、 D、14. 如图,在中, , 将绕顶点C顺时针旋转得到 , D是的中点,连接BD,若 , , 则线段的最大值为( ) A、 B、 C、3 D、415. 如图,已知点A(-8,0)、B(2,0),点C在直线y=-0.75x+4上,则使△ABC是直角三角形的点C的个数为( )
A、 B、 C、3 D、415. 如图,已知点A(-8,0)、B(2,0),点C在直线y=-0.75x+4上,则使△ABC是直角三角形的点C的个数为( ) A、1 B、2 C、3 D、416. 如图,等腰梯形的腰长为3,正方形的边长为1,它的一边在上,且顶点A与M重合.现将正方形在梯形的外面沿边进行翻滚,翻滚到有一个顶点与N重合即停止滚动,求正方形在翻滚过程中点A所经过的路线长( )
A、1 B、2 C、3 D、416. 如图,等腰梯形的腰长为3,正方形的边长为1,它的一边在上,且顶点A与M重合.现将正方形在梯形的外面沿边进行翻滚,翻滚到有一个顶点与N重合即停止滚动,求正方形在翻滚过程中点A所经过的路线长( )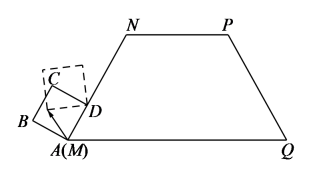 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
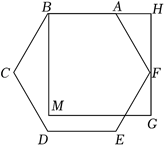
17. 因式分解: .18. 如图,正六边形ABCDEF的顶点A、F分别在正方形BMGH的边BH、GH上.若正方形BMGH的边长为6,则正六边形ABCDEF的边长为 .
 19. 在平面直角坐标系中,直线 , 经过点 , 且与坐标轴围成的三角形的面积是9,与曲线的图象G交于A,B两点.(1)、则直线的表达式为;(2)、横、纵坐标都是整数的点叫作整点.记图象G在点A、B之间的部分与线段AB围成的区域(不含边界)为W.则区域W内的整点的坐标是 .
19. 在平面直角坐标系中,直线 , 经过点 , 且与坐标轴围成的三角形的面积是9,与曲线的图象G交于A,B两点.(1)、则直线的表达式为;(2)、横、纵坐标都是整数的点叫作整点.记图象G在点A、B之间的部分与线段AB围成的区域(不含边界)为W.则区域W内的整点的坐标是 .三、解答题
-
20. 请你根据王老师所给的内容(如表),完成下列各小题.
我们定义一个关于非零常数a,b的新运算,规定:a〇b=ax+by.例如:3〇2=3x+2y.
(1)、如果x=5,2〇4=-18,求y的值;(2)、若1〇1=8,4〇2=20,求x,y的值.21. 如图,在数轴上点 , 表示的数分别为-2,1,为点左侧上的一点,它表示的数为 . (1)、用含的代数式表示的值.(2)、若以 , , 的长为边长能构成等腰三角形,请求出符合条件的的值.22. 河北省某校为了增强学生的体质,引导同学们积极参加体育锻炼,学校购买了一批跳绳供学生借用,现从九年级随机抽取了部分学生对跳绳进行测试,并绘制了如下的两幅不完整的统计表和统计图.请根据相关信息,解答下列问题.
(1)、用含的代数式表示的值.(2)、若以 , , 的长为边长能构成等腰三角形,请求出符合条件的的值.22. 河北省某校为了增强学生的体质,引导同学们积极参加体育锻炼,学校购买了一批跳绳供学生借用,现从九年级随机抽取了部分学生对跳绳进行测试,并绘制了如下的两幅不完整的统计表和统计图.请根据相关信息,解答下列问题.一分钟跳绳成绩的频数统计表
组别
跳绳次数分段
频数
A
n
B
70
C
76
D
34
一分钟跳绳成绩的扇形统计图
 (1)、本次接受随机抽样调查的学生人数为多少人?统计表中的n的值是多少?扇形统计图中B组所对的圆心角是多少度?(2)、求抽取学生一分钟跳绳成绩的中位数所在的组别;(3)、现在指定两名男生和两名女生负责跳绳发放和整理工作,若两人一组,随机组合,请用画树状图或列表法求出恰好分组是一男一女的概率是多少?23. 如图,将两个完全相同的三角形纸片和重合放置,其中 , .
(1)、本次接受随机抽样调查的学生人数为多少人?统计表中的n的值是多少?扇形统计图中B组所对的圆心角是多少度?(2)、求抽取学生一分钟跳绳成绩的中位数所在的组别;(3)、现在指定两名男生和两名女生负责跳绳发放和整理工作,若两人一组,随机组合,请用画树状图或列表法求出恰好分组是一男一女的概率是多少?23. 如图,将两个完全相同的三角形纸片和重合放置,其中 , .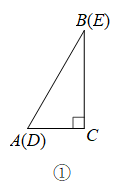
 (1)、操作发现
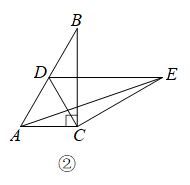
(1)、操作发现如图②,固定 , 使绕点C旋转,当点D恰好落在边上时,
①求线段与的位置关系;
②设的面积为 , 的面积为 , 求与的数量关系.
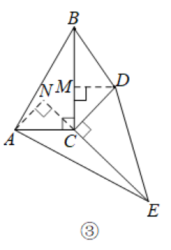
(2)、猜想论证当绕点C旋转到如图③所示的位置时,小明猜想(1)中与的数量关系仍然成立,并尝试分别作出了和中、边上的高,请你证明小明的猜想.
24. 定义:如果二次函数 , ( , 、、是常数)与 , 、、是常数)满足 , , , 则这两个函致互为“旋转函数”.例如:求函数的“旋转函数”,由函数可知, , , . 根据 , , 求出、、就能确定这个函数的“旋转函数”.请思考并解决下面问题:
(1)、写出函数的“旋转函数”;(2)、若函数与互为“旋转函数”,求的值;(3)、已知函数的图象与x轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是、、 , 试求证:经过点、、的二次函数与互为“旋转函数”.25. 在体育学科的女子800米耐力测试中,某考点的王芳同学所跑的路程s(米)与所用时间t(秒)之间的函数图象为折线 . 和她同时起跑的李梅同学前600米的速度保持在5米/秒,后来因为体力下降,速度变慢,但还保持匀速奔跑,结果和王芳同学同时到达终点. (1)、在图中画出李梅同学所跑的路程s(米)与所用时间t(秒)之间的函数图象;(2)、求王芳同学测试中的最快速度;(3)、求李梅同学在起跑后多少秒追上王芳同学,这时她距离终点还有多少米?26. 如图,的半径为 , 正三角形的顶点B的坐标为 , 顶点A在上运动.
(1)、在图中画出李梅同学所跑的路程s(米)与所用时间t(秒)之间的函数图象;(2)、求王芳同学测试中的最快速度;(3)、求李梅同学在起跑后多少秒追上王芳同学,这时她距离终点还有多少米?26. 如图,的半径为 , 正三角形的顶点B的坐标为 , 顶点A在上运动. (1)、当点A在x轴正半轴上时,求点C的坐标;(2)、点A在运动过程中,是否存在直线与相切的位置关系?若存在,请直接写出点C的坐标;(3)、设点A的横坐标为x,的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值.
(1)、当点A在x轴正半轴上时,求点C的坐标;(2)、点A在运动过程中,是否存在直线与相切的位置关系?若存在,请直接写出点C的坐标;(3)、设点A的横坐标为x,的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值.