天津市南开区2022年九年级二模考试数学试卷

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $(- 2)^{3}$ 的结果是（）

A、6 B、-6 C、-8 D、9

查看试题解析
2. $3 \tan 30 °$ 的值等于（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{3}$ C、3 D、1

查看试题解析
3. 今年4月16日，神舟十三号载人飞船返回舱在东风着陆场预定区域安全着陆，三位航天员顺利返回地面，神舟十三号载人飞行任务取得圆满成功．已知神舟十三号飞行过程中近地距离 $200000 m$ ，远地距离 $356000 m$ ．将“356000”用科学记数法表示为（）

A、 $35.6 \times 1 0^{4}$ B、 $3.56 \times 1 0^{5}$ C、 $3.56 \times 1 0^{6}$ D、 $0.356 \times 1 0^{6}$

查看试题解析
4. “仁、义、礼、智、信”是中华民族传统美德的核心价值理念和基本要求，是我们每个公民都应遵循的、最重要的五种社会道德规范．如图是“仁、义、礼、智、信”这五个字的首字母，其中既不是轴对称图形，也不是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，由8个大小相同的正方体搭成的几何体，其俯视图是（）

A、 B、 C、 D、

查看试题解析
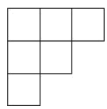6. 下列各数中介于6和7之间的数是（）

A、 $\sqrt{15}$ B、 $\sqrt{33}$ C、 $\sqrt{39}$ D、 $\sqrt{53}$

查看试题解析
7. 方程组 ${\begin{array}{l} 3 x + 4 y = 2 \\ 2 x - y = 5 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$

查看试题解析
8. 化简 $\frac{4 x - 3 y}{x^{2} - y^{2}} - \frac{x - 2 y}{y^{2} - x^{2}}$ 的结果是（）

A、 $\frac{5}{x - y}$ B、 $\frac{5}{x + y}$ C、 $\frac{5}{x^{2} - y^{2}}$ D、 $\frac{3 x + y}{x^{2} - y^{2}}$

查看试题解析
9. 若点(x₁ ， 3) ，(x₂ ， 1) ，(x₃ ， −3)在反比例函数y= $\frac{k}{x}$ (k<0)的图象上，则x₁ ， x₂ ， x₃的大小关系是（）

A、 $x_{2} < x_{1} < x_{3}$ B、 $x_{3} < x_{2} < x_{1}$ C、 $x_{1} < x_{2} < x_{3}$ D、 $x_{3} < x_{1} < x_{2}$

查看试题解析
10. 如图，在平面直角坐标系中，四边形ABCD为正方形，点A的坐标为 $(0 ， 2)$ ，点B的坐标为 $(4 ， 0)$ ，点E为对角线的交点，点F与点E关于y轴对称，则点F的坐标为（）

A、 $(- 2 ， 3)$ B、 $(3 ， - 3)$ C、 $(- 3 ， 2)$ D、 $(- 3 ， 3)$

查看试题解析
11. 如图，在 $△ A B C$ 中， $∠ B A C = 90 ° ， A B = 3 c m ， A C = 4 c m$ ，将 $△ A B C$ 沿直线 $B C$ 向右平移 $2.5 c m$ 后，得到 $△ D E F$ ，连接 $A E ， A D$ ．下列结论错误的是（）

A、 $A C ∥ D F$ B、 $A D ∥ C F$ C、 $C F = 3 c m$ D、 $D E ⊥ A C$

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 中的x与y的部分对应值如表：
x
…
-1
0
3
…
y
…
n
-3
-3
…
当 $n > 0$ 时，以下结论：① $b c > 0$ ；②当 $x > 2$ 时，的值随x值的增大而增大；③ $n > 4 a$ ；④当 $n = 1$ 时，关于x的一元二次方程 $a x^{2} + (b + 1) x + c = 0$ 的解是 $x_{1} = - 1 ， x_{2} = 3$ ；其中结论一定正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

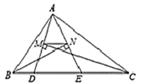
13. 将多项式 $3 a^{2} - 6 a b + 3 b^{2}$ 分解因式，其结果是．

查看试题解析
14. 计算 $(\sqrt{13} + 3) (\sqrt{13} - 3)$ 的结果等于．

查看试题解析
15. 有五张背面完全相同的卡片，正面分别标有数字-2，-1，0，1，2，把这5张卡片背面朝上，随机抽取一张，则抽到卡片上的数是负数的概率为．

查看试题解析
16. 若将直线 $y = k x (k \neq 0)$ 的图象向上平移 $3$ 个单位后经过点 $(2, 7)$ ，则平移后直线的解析式．

查看试题解析
17. 如图，△ABC的周长为19，点D、E在边BC上，∠ABC的平分线垂直于AE，垂足为N ，∠ACB的平分线重直于AD，垂足为M，若BC=7，则MN的长度为.

查看试题解析
18. 如图，在每个小正方形的边长为1的网格中，O为格点，⊙ $O$ 经过格点A．

(1)、⊙ $O$ 的周长等于；

(2)、请用无刻度的直尺，在如图所示的网格中，画出⊙ $O$ 的内接等边 $△ A B C$ ，并简要说明点B，C的位置是如何找到的（不要求证明） ▲ ．

查看试题解析

三、解答题

19. 解不等式组组 ${\begin{array}{l} 5 x + 1 > 3 x - 1 ① \\ 6 x - 4 < 2 (6 - x) ② \end{array}$ ，请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来：

(4)、原不等式组的解集为．

查看试题解析
20. 小文同学统计了他所在小区居民每周微信阅读的时间，并绘制了如下的统计图①和图②．请根据相关信息，解答下列问题：

(1)、本次小宁调查的小区人数为，图①中m的值为；

(2)、求统计的这组人员阅读时间数据的平均数、众数和中位数．

查看试题解析
21. 如图， $A B$ 为 $⊙ O$ 的直径， $B D$ 与 $⊙ O$ 相切于点 $B$ ， $C$ 是圆上一点．

(1)、如图 $1$ ，若 $∠ D B C = 2 4^{∘}$ ，求 $∠ A$ 的度数；

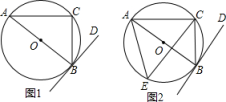(2)、如图 $2$ ， $C E$ 平分 $∠ A C B$ 与 $⊙ O$ 交于点 $E$ ，若 $B C = 2$ ， $A C = 4$ ，求 $A E$ 的长．

查看试题解析
22. “天津之眼”是世界上唯一一个桥上瞰景的摩天轮，小宇同学乘坐摩天轮时发现，当小宇在摩天轮客舱中上升到点B位置时，测得C处的俯角是66°，测得A处俯角63.6°，已知摩天轮最低点A距离地面的高度AC=10米，求小宇此时所在B处距离地面高度．（参考数据：tan63.6°≈2.0，tan66°≈2.25．）

查看试题解析
23. 已知小明家、菜地、玉米地在同一条直线上．菜地离小明家1.1千米，玉米地离小明家2千米．周末小明从家去菜地浇水10分钟，又继续前行去玉米地锄草，然后从玉米地返回家中给出的图象反映了小明离家的距离y（千米）与离开家的时间x（分）之间的对应关系．
请根据以上信息，解答下列问题：

(1)、填表：
离开家的时间/分
15
25
37
40
60
离家的距离/千米
1.1
2

(2)、填空：
①小明从家到菜地用了分钟；
②小明给玉米地锄草用了分钟；
③小明从玉米地回家的平均速度是千米/分；
④当小明离家的距离为1.5千米时，他离开家的时间为分钟；

(3)、当 $25 \leq x \leq 80$ 时，请直接写出y关于x的函数解析式．

查看试题解析
24. 面直角坐标系中，O为原点，点 $A (12 ， 0)$ ，点 $B (0 ， 5)$ ，线段 $A B$ 的中点为点C．将 $△ A B O$ 绕着点B逆时针旋转，点O对应点为 $O_{1}$ ，点A的对应点为 $A_{1}$ ．

(1)、如图①，当点 $O_{1}$ 恰好落在 $A B$ 上时，
①此时 $C O_{1}$ 的长为 ▲ ；
②点P是线段 $O A$ 上的动点，旋转后的对应点为 $P_{1}$ ，连接 $B P_{1} ， P O_{1}$ ，试求 $B P_{1} + P O_{1}$ 最小时点P的坐标；

(2)、如图②，连接 $C A_{1} ， C O_{1}$ ，则在旋转过程中， $△ C A_{1} O_{1}$ 的面积是否存在最大值？若存在，直接写出最大值，若不存在，说明理由．

查看试题解析
25. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴相交于A，B两点（点A位于点B的左侧），与y轴相交于点C，M是抛物线的顶点，直线 $x = 1$ 是抛物线的对称轴，且点C的坐标为 $(0 ， 3)$ ．

(1)、求抛物线的解析式；

(2)、已知P为线段 $M B$ 上一个动点，过点P作 $P D ⊥ x$ 轴于点D．若 $P D = m ， △ P C D$ 的面积为S．
①求S与m之间的函数关系式，并写出自变量m的取值范围；
②当S取得最大值时，求点P的坐标．

(3)、在（2）的条件下，在线段 $M B$ 上是否存在点P，使 $△ P C D$ 为等腰三角形？如果存在，直接写出满足条件的点P的坐标；如果不存在，请说明理由．

查看试题解析

x	…	-1	0	3	…
y	…	n	-3	-3	…

离开家的时间/分	15	25	37	40	60
离家的距离/千米	1.1		2