山西2022年中考模拟百校联考(三)数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 计算的结果是( )A、-3 B、3 C、-12 D、122. 下列四个图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列几何体都是由大小相同的小正方体组成,其中左视图与主视图相同的几何体是( )A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列几何体都是由大小相同的小正方体组成,其中左视图与主视图相同的几何体是( )A、 B、
B、 C、
C、 D、
D、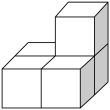 5. 2022年“世界水日”和“中国水周”的活动主题为“推进地下水超采综合治理,复苏河湖生态环境”统计数据显示2020年我国地下水开采总量为892.5亿立方米,较2012年减少约242亿立方米.其中892.5亿用科学记数法可以表示为( )
5. 2022年“世界水日”和“中国水周”的活动主题为“推进地下水超采综合治理,复苏河湖生态环境”统计数据显示2020年我国地下水开采总量为892.5亿立方米,较2012年减少约242亿立方米.其中892.5亿用科学记数法可以表示为( ) A、 B、 C、 D、6. 如图是一副三角板,其中 , , , 若点B与点F重合,点D在AB边上,AC与EF交于点G,则的度数为( )
A、 B、 C、 D、6. 如图是一副三角板,其中 , , , 若点B与点F重合,点D在AB边上,AC与EF交于点G,则的度数为( ) A、45° B、60° C、65° D、75°7. 如图,内接于⊙O,AB为⊙O直径,点D是⊙O上的一点(点C,D在AB的两侧),连接AD,CD.若 , 则( )
A、45° B、60° C、65° D、75°7. 如图,内接于⊙O,AB为⊙O直径,点D是⊙O上的一点(点C,D在AB的两侧),连接AD,CD.若 , 则( ) A、36° B、54° C、64° D、72°8. 物理课上小刚在探究弹簧测力计的“弹簧的长度与受到的拉力之间的关系”时,在弹簧的弹性限度内,通过实验获得下面的一组数据.在弹簧的弹性限度内,若拉力为7.5N,则弹簧长度为( )
A、36° B、54° C、64° D、72°8. 物理课上小刚在探究弹簧测力计的“弹簧的长度与受到的拉力之间的关系”时,在弹簧的弹性限度内,通过实验获得下面的一组数据.在弹簧的弹性限度内,若拉力为7.5N,则弹簧长度为( )
拉力/N
0
1
2
3
4
5
6
弹簧长度/cm
10.0
12.0
14.0
16.0
18.0
20.0
22.0
A、24cm B、25cm C、25.5cm D、26cm9. 《九章算术》有题曰:“今有五雀,六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕雀重一斤.问燕雀一枚各重几何?”其大意是:“现在有5只雀,6只燕,分别集中放在天平上称重,聚在一起的雀重燕轻.将一只雀一只燕交换位置而放,重量相等.5只雀、6只燕重量共一斤,问雀和燕各重多少?”古代记1斤为16两,则设1只雀 两一只燕 两,可列出方程( ).A、 B、 C、 D、10. 如图,在中, , , AO是的中线,以O为圆心,OA长为半径作圆,分别交AB,AC于点D,E,交BC于点F,G.则图中阴影部分的面积为( )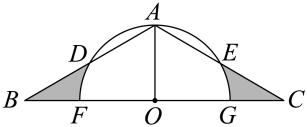 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: = .12. 如图,用若干相同的小棒拼成含正五边形的图形,拼第1个图形需要5根小棒;拼第2个图形需要9根小棒;拼第3个图形需要13根小棒……按此规律,拼第n个图形需要根小棒(用含n的代数式表示).
 13. 一个不透明的袋子里有白球和红球各两个,这些小球除颜色以外完全相同,小明从袋子里随机摸出一个小球记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到白球的概率为 .14. 2022年,北京成功举办第24届冬季奥运会后,很多学校都开展了冰雪项目的学习活动.如图,一位同学乘滑雪板沿坡度为的斜坡滑行30米,则他下降的高度为米.
13. 一个不透明的袋子里有白球和红球各两个,这些小球除颜色以外完全相同,小明从袋子里随机摸出一个小球记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到白球的概率为 .14. 2022年,北京成功举办第24届冬季奥运会后,很多学校都开展了冰雪项目的学习活动.如图,一位同学乘滑雪板沿坡度为的斜坡滑行30米,则他下降的高度为米. 15. 如图,在 ▱ ABCD中,对角线AC,BD相交于点O, , , , 的平分线分别交AC,BC于点E,F.则线段OE的长为 .
15. 如图,在 ▱ ABCD中,对角线AC,BD相交于点O, , , , 的平分线分别交AC,BC于点E,F.则线段OE的长为 .
三、解答题
-
16.(1)、计算: .(2)、下面是小明同学分式化简的过程,请认真阅读并完成任务.
解:
……第一步
……第二步
. ……第三步
①小明的解答过程从第 ▲ 步开始出错;
②请你写出正确的解答过程.
17. 如图,一次函数的图象分别与x轴、y轴交于点C,D,与反比例函数的图象交于 , 两点. (1)、求一次函数和反比例函数的表达式.(2)、若x轴上存在一点P,使的面积为6,求点P的坐标.18. 如图,在中,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线,交BC于点E,连接BD.
(1)、求一次函数和反比例函数的表达式.(2)、若x轴上存在一点P,使的面积为6,求点P的坐标.18. 如图,在中,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线,交BC于点E,连接BD.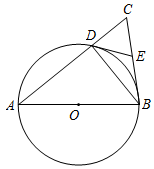 (1)、判断与的数量关系,并说明理由.(2)、若 , , 求的长.19. 2022年5月5日中国共产主义青年团成立100周年,某校开展“赓继红色血脉,敬致百年风华”系列活动.在活动前某校团委随机抽取部分学生调查其对“共青团”的了解情况,并将了解程度由高到低分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.对调查结果整理后绘制了如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)、判断与的数量关系,并说明理由.(2)、若 , , 求的长.19. 2022年5月5日中国共产主义青年团成立100周年,某校开展“赓继红色血脉,敬致百年风华”系列活动.在活动前某校团委随机抽取部分学生调查其对“共青团”的了解情况,并将了解程度由高到低分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.对调查结果整理后绘制了如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题: (1)、被调查学生的人数为 .(2)、补全条形统计图.(3)、在扇形统计图中的“C.基本了解”对应的扇形圆心角的度数为 .(4)、已知该校有800名学生,估计对“共青团”知识了解程度达到“C.基本了解”及以上的学生有多少人.20. 2021年复建后的“首义门”,坐落于太原五一广场,它气势恢宏,庄严肃穆.城台BH高11.7米,上部的城楼为四重檐歇山顶楼阁式建筑,阁楼主体为全木质卯榫结构.某校“综合与实践”小组要测量木质楼阁AB的高度,由于底部不能到达,他们在点C处测得楼阁顶部A的仰角为 , 沿CH方向前行41.5米到达点D处,测得城台顶部B的仰角为 . 其点A,B,H,D,C在同一竖直平面内.求木质楼阁AB的高度(结果保留1位小数.参考数据: , , , ).
(1)、被调查学生的人数为 .(2)、补全条形统计图.(3)、在扇形统计图中的“C.基本了解”对应的扇形圆心角的度数为 .(4)、已知该校有800名学生,估计对“共青团”知识了解程度达到“C.基本了解”及以上的学生有多少人.20. 2021年复建后的“首义门”,坐落于太原五一广场,它气势恢宏,庄严肃穆.城台BH高11.7米,上部的城楼为四重檐歇山顶楼阁式建筑,阁楼主体为全木质卯榫结构.某校“综合与实践”小组要测量木质楼阁AB的高度,由于底部不能到达,他们在点C处测得楼阁顶部A的仰角为 , 沿CH方向前行41.5米到达点D处,测得城台顶部B的仰角为 . 其点A,B,H,D,C在同一竖直平面内.求木质楼阁AB的高度(结果保留1位小数.参考数据: , , , ). 21. 下面是小亮学习了“分式方程的应用”后所作的课堂学习笔记,请认真阅读并完成相应的任务.
21. 下面是小亮学习了“分式方程的应用”后所作的课堂学习笔记,请认真阅读并完成相应的任务.题目:某商店准备购进甲、乙两种商品,甲种商品每件的进价比乙种商品每件的进价多20元,用2000元购进甲种商品和用1200元购进乙种商品的数量相同.求甲、乙两种商品每件的进价各是多少元.
方法
分析问题
列出方程
解法一
设……
等量关系:甲商品数量=乙商品数量
解法二
设……
等量关系:甲商品进价-乙商品进价=20
任务:
(1)、解法一所列方程中的x表示 , 解法二所列方程中的x表示 .A.甲种商品每件进价x元 B.乙种商品每件进价x元 C.甲种商品购进x件
(2)、根据以上解法可求出甲种商品的进价为元/件,乙种商品的进价为元/件.(3)、若商店将甲种商品每件的售价定为80元,乙种商品每件的售价定为45元.商店计划用不超过1440元的资金购进甲、乙两种商品共40件,当购进的甲、乙两种商品全部售出后,请求出该商店获得最大的利润W.(利润=售价-进价)22. 综合与时间问题情境:如图1,在正方形ABCD中,点E是对角线AC上一点,连接BE,过点E分别作AC,BE的垂线,分别交直线BC,CD于点F,G.试猜想线段BF和CG的数量关系,并加以证明.
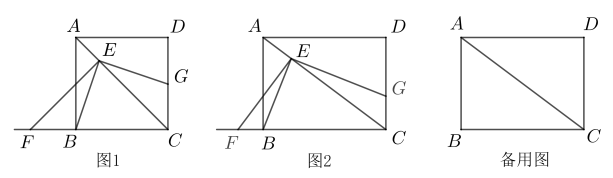 (1)、数学思考:请解答上述问题.(2)、问题解决:如图2,在图1的条件下,将“正方形ABCD”改为“矩形ABCD”,其他条件不变.若 , , 求的值.(3)、问题拓展:在(2)的条件下,当点E为AC的中点时,请直接写出的面积.23. 综合与探究
(1)、数学思考:请解答上述问题.(2)、问题解决:如图2,在图1的条件下,将“正方形ABCD”改为“矩形ABCD”,其他条件不变.若 , , 求的值.(3)、问题拓展:在(2)的条件下,当点E为AC的中点时,请直接写出的面积.23. 综合与探究如图,二次函数y=ax2+bx+4的图象与x轴分别交于点A(−2,0),B(4,0),点E是x轴正半轴上的一个动点,过点E作直线PE⊥x轴,交抛物线于点P,交直线BC于点F.

 (1)、求二次函数的表达式.(2)、当点E在线段OB上运动时(不与点O,B重合),恰有线段 , 求此时点P的坐标.(3)、试探究:若点Q是y轴上一点,在点E运动过程中,是否存在点Q,使得以点C,F,P,Q为顶点的四边形为菱形,若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、求二次函数的表达式.(2)、当点E在线段OB上运动时(不与点O,B重合),恰有线段 , 求此时点P的坐标.(3)、试探究:若点Q是y轴上一点,在点E运动过程中,是否存在点Q,使得以点C,F,P,Q为顶点的四边形为菱形,若存在,直接写出点Q的坐标;若不存在,请说明理由.