山西省吕梁市交城县2022年九年级中考第二次模拟考数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. -2的绝对值是()
A、2 B、 C、 D、-22. 将下列长度的三条线段首尾顺次相接,不能组成三角形的是( )A、1, , B、5,12,13 C、5,7,12 D、4,4,63. 下列计算正确的是( )A、 B、 C、 D、4. 下面几何体是由4个大小相同的小正方体搭成的,关于该几何体的三视图,下列说法正确的是( ) A、左视图和主视图相同 B、左视图和俯视图相同 C、主视图和俯视图相同 D、主视图、俯视图和左视图各不相同5. 今年春季,国内新一轮疫情呈现出多点散发、局部暴发态势,我省太原市、部分县(市、区)出现了不同程度的新冠肺炎感染病例,关于在此次疫情防控调查中,适合采用抽样调查的是( )
A、左视图和主视图相同 B、左视图和俯视图相同 C、主视图和俯视图相同 D、主视图、俯视图和左视图各不相同5. 今年春季,国内新一轮疫情呈现出多点散发、局部暴发态势,我省太原市、部分县(市、区)出现了不同程度的新冠肺炎感染病例,关于在此次疫情防控调查中,适合采用抽样调查的是( ) A、对某厂家生产的某批次口罩的合格情况的调查 B、对出入各机场、高速口的旅客进行健康码、行程码的调查 C、对某高风险地区居民的核酸检测情况的调查 D、对“某阳性新冠肺炎感染者”的密接者的调查6. 一元二次方程的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、只有一个实数根7. 中国结(图1)代表着中华民族的传统文化,象征着中国人民对美好生活的祝福和对真善美的追求.图2是由边长为1的小正方形设计的一组有规律的中国结图案,按此规律,则第个图案中边长为1的小正方形的个数是( )
A、对某厂家生产的某批次口罩的合格情况的调查 B、对出入各机场、高速口的旅客进行健康码、行程码的调查 C、对某高风险地区居民的核酸检测情况的调查 D、对“某阳性新冠肺炎感染者”的密接者的调查6. 一元二次方程的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、只有一个实数根7. 中国结(图1)代表着中华民族的传统文化,象征着中国人民对美好生活的祝福和对真善美的追求.图2是由边长为1的小正方形设计的一组有规律的中国结图案,按此规律,则第个图案中边长为1的小正方形的个数是( ) A、 B、 C、 D、8. 小孔成像是由于光在均匀介质中沿直线传播而形成的一种物理现象.两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因.图1是某次小孔成像实验图,其原理可以用图2所示的平面图形表示.若在这次实验中,蜡烛火焰的高度为 , 小孔到光屏的距离为 , 蜡烛到小孔的距离为 , 则蜡烛在光屏上所成实像的高度 . 其中根据的数学原理是( )
A、 B、 C、 D、8. 小孔成像是由于光在均匀介质中沿直线传播而形成的一种物理现象.两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因.图1是某次小孔成像实验图,其原理可以用图2所示的平面图形表示.若在这次实验中,蜡烛火焰的高度为 , 小孔到光屏的距离为 , 蜡烛到小孔的距离为 , 则蜡烛在光屏上所成实像的高度 . 其中根据的数学原理是( )
墨子,名翟,公元前476或480年—公元前390或420年.我国古代教育家、思想家、哲学家.
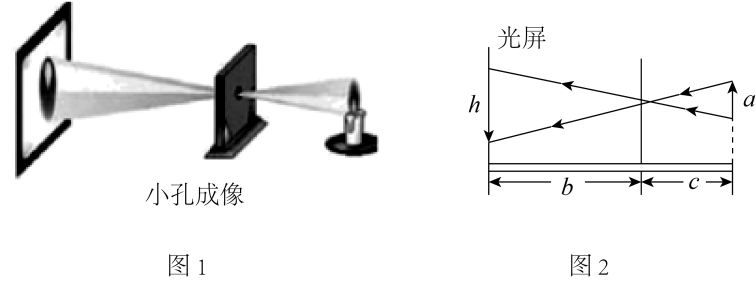 A、图形的旋转 B、图形的轴对称 C、图形的平移 D、图形的相似9. 如图,在菱形中, , 以为直径作 , 分别与菱形的边相交于点 , , , . 若 , 则图中阴影部分的面积为( )
A、图形的旋转 B、图形的轴对称 C、图形的平移 D、图形的相似9. 如图,在菱形中, , 以为直径作 , 分别与菱形的边相交于点 , , , . 若 , 则图中阴影部分的面积为( ) A、 B、 C、 D、10. 如图,与相切于点 , 与交于点 , 若 , . 则的长度为( )
A、 B、 C、 D、10. 如图,与相切于点 , 与交于点 , 若 , . 则的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在五边形中, , , , 则的度数是 .
 12. 将抛物线先向左平移2个单位长度,再向上平移个单位长度.若得到的抛物线经过点 , 则的值是 .13. 丝绸之路起始于古代中国,是连接亚洲、非洲和欧洲的古代商业贸易路线,是东方与西方之间经济、政治、文化交流的主要道路.小明妈妈搜集到如下四张《丝绸之路特种邮票》,分别是:A:汉·凸瓣纹银盒;B:唐·长沙窑青釉褐斑模印贴花椰枣纹执壶;C:五代十国·波斯孔雀蓝釉陶瓶;D:宋·龙泉窑青釉菊瓣纹盘.妈妈让小明随机抽取其中的两张作为给他的奖励.则小明恰好抽中“唐·长沙窑青釉褐斑模印贴花椰枣纹执壶”和“宋·龙泉窑青釉菊瓣纹盘”的概率是 .
12. 将抛物线先向左平移2个单位长度,再向上平移个单位长度.若得到的抛物线经过点 , 则的值是 .13. 丝绸之路起始于古代中国,是连接亚洲、非洲和欧洲的古代商业贸易路线,是东方与西方之间经济、政治、文化交流的主要道路.小明妈妈搜集到如下四张《丝绸之路特种邮票》,分别是:A:汉·凸瓣纹银盒;B:唐·长沙窑青釉褐斑模印贴花椰枣纹执壶;C:五代十国·波斯孔雀蓝釉陶瓶;D:宋·龙泉窑青釉菊瓣纹盘.妈妈让小明随机抽取其中的两张作为给他的奖励.则小明恰好抽中“唐·长沙窑青釉褐斑模印贴花椰枣纹执壶”和“宋·龙泉窑青釉菊瓣纹盘”的概率是 .A.
 B.
B. C.
C. D.
D. 14. 某指示牌形状如图1所示,图2是其平面示意图,若 , , 米,则点到地面的距离等于米.(参考数据: , , ).
14. 某指示牌形状如图1所示,图2是其平面示意图,若 , , 米,则点到地面的距离等于米.(参考数据: , , ).
 15. 如图,在矩形中, , , 在上,且 , 在的延长线上,且 , 则线段的长度为 .
15. 如图,在矩形中, , , 在上,且 , 在的延长线上,且 , 则线段的长度为 .
三、解答题
-
16.(1)、计算: .(2)、阅读下面解方程的过程,并完成相应学习任务:
解:去分母,方程两边同乘4,得
. 第一步
去括号,得
. 第二步
移项,得
. 第三步
合并同类项,得
. 第四步
任务:
①上面解方程的最终目的是使方程逐步变形为“(已知数)”的形式,体现的数学思想是 . (填出字母序号即可)
A.方程思想 B.转化思想 C.特殊到一般的思想
②上面解方程的过程,从第步开始出现错误,错误原因是 .
③移项的依据是 .
④方程的正确解是 .
17. 化简: .18. 如图,一次函数的图象与轴交于点 , 与轴交于点 , 与反比例函数的图象交于点 . 点在轴上,并且四边形是平行四边形. (1)、求反比例函数的表达式;(2)、根据图象,直接写出当时,的取值范围.19. 阅读下列材料,并完成相应的学习任务:
(1)、求反比例函数的表达式;(2)、根据图象,直接写出当时,的取值范围.19. 阅读下列材料,并完成相应的学习任务:一次有意义的动手实践活动——在格点图中巧作角平分线
实践背景
在一次动手实践课上,老师提出如下问题:在如图1所示由边长为1的小正方形组成的格点图中,点 , , 都在小正方形的顶点处,仅用无刻度的直尺作出的角平分线.
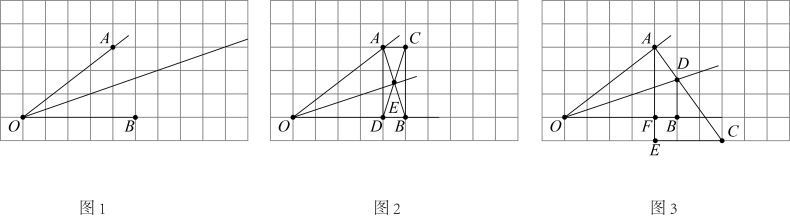
成果展示
小明、小亮展示了如下作法:
小明:如图2,在格点图中取格点 , . 连接 , 交于点 . 作出射线 .
∵四边形是矩形,∴(依据1).
∵ , ∴平分 .
小亮:如图3,在格点图中取格点 . 连接 , 与小正方形的边交于点 . 则 .
∵ , .
∴(依据2).
∴ , 即平分 .
学习任务:
(1)、实践反思:①请填写出上述材料中的依据1和依据2.
依据1: ▲ ;依据2: ▲ .
②请根据小亮的作法,证明 .
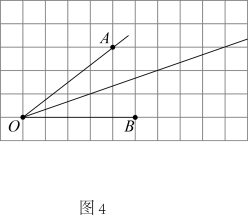
(2)、创新再探请你根据实践背景问题要求,采用不同于小明和小亮的作法,描出作图过程中的所取得的点,作出的角平分线(不写作法,不需要说明理由).
 20. 近年来,随着中国消费市场线上线下的快速融合发展,三线、四线城市、农村等市场的潜力得到激发,我国快递业务量持续保持中高速发展.下图是《2015年—2021年中国快递服务企业业务量及与上一年同期相比增长率》与《2020年中国快递公司所占市场份额分布情况》统计图.
20. 近年来,随着中国消费市场线上线下的快速融合发展,三线、四线城市、农村等市场的潜力得到激发,我国快递业务量持续保持中高速发展.下图是《2015年—2021年中国快递服务企业业务量及与上一年同期相比增长率》与《2020年中国快递公司所占市场份额分布情况》统计图.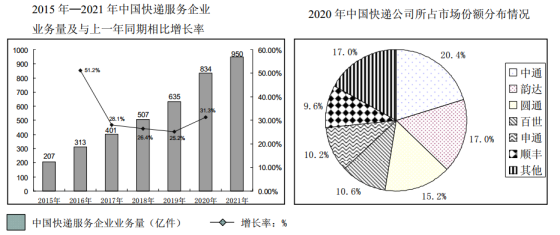
请你根据统计图表信息,解决下列问题:
(1)、2015年—2021年我国快递业务量的中位数是亿件,2021年与2020年同期相比,快递业务量的增长率是 . (精确到0.1%)(2)、如果2021年我国快递公司所占市场份额与2020年相比基本保持不变,则2021年韵达快递公司的业务量大约是亿件.(3)、我省快递公司运费的计算方法是:快递运费=首重价格+续重价格.(首重价格指快递质量不超过1千克时的价格;续重价格指快递质量超过1千克时,超过部分的价格.并且首重和续重不足1千克的部分都按1千克计算).现有 , 两家快递公司的收费标准如下:小亮计划在 , 两个快递公司选择其一,将4.6千克的物品邮往某地,请你通过计算说明,他选择哪家公司比较合算?快递公司
首重
续重
13元
10元/千克
10元
12元/千克
21. 在北京冬奥会、冬残奥会举办期间,吉祥物“冰墩墩”、“雪容融”一举成为顶流,憨态可掬的形象赢得了无数海内外粉丝的喜爱,全国掀起了购买“冰墩墩”、“雪容融”的热潮.某网店各花费6000元购进了一批“冰墩墩”、“雪容融”进行销售,其中每件“冰墩墩”的进价比“雪容融”贵20元,购进的“冰墩墩”的数量是“雪容融”的 .
 (1)、求每件“冰墩墩”、“雪容融”的进价分别是多少元;(2)、该网店计划先以整套(一个冰墩墩和一个雪容融搭配为一套)的方式进行销售,再将多余的雪容融以25%的利润率进行售卖,若将所有的冰墩墩和雪容融销售完毕后,商家想获得的总利润不低于6375元,则每套冰墩墩和雪容融的售价至少为多少元?22. 综合与实践
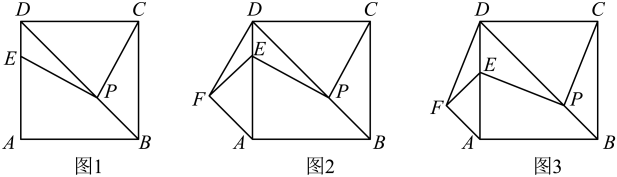
(1)、求每件“冰墩墩”、“雪容融”的进价分别是多少元;(2)、该网店计划先以整套(一个冰墩墩和一个雪容融搭配为一套)的方式进行销售,再将多余的雪容融以25%的利润率进行售卖,若将所有的冰墩墩和雪容融销售完毕后,商家想获得的总利润不低于6375元,则每套冰墩墩和雪容融的售价至少为多少元?22. 综合与实践问题情境:数学活动课上,老师提出如下问题:如图1,在正方形中,是对角线上一点,将直线以点为中心逆时针旋转 , 旋转后的直线与交于点 . 求证: .
 (1)、问题解决:
(1)、问题解决:请你解决老师提出的问题;
(2)、数学思考:如图2,“兴趣小组”的同学将沿射线的方向平移到 , 点的对应点为 . 连接 . 他们认为: , . 他们的认识是否正确?请说明理由.
(3)、创新探究“创新小组”在“兴趣小组”所提问题的基础上,又提出如下新问题,请你思考并解决该问题:如图3,若垂直平分 , , 则线段的长度是 . (直接写出答案即可)
23. 综合与探究如图,二次函数与轴交于 , 两点,与轴交于点 . 点是射线上的动点,过点作 , 并且交轴于点 .
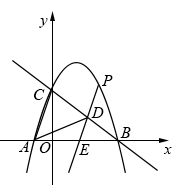
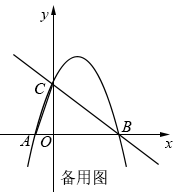 (1)、请直接写出 , , 三点的坐标及直线的函数表达式;(2)、当平分时,求出点的坐标;(3)、当点在线段上运动时,直线与抛物线在第一象限内交于点 , 则线段是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
(1)、请直接写出 , , 三点的坐标及直线的函数表达式;(2)、当平分时,求出点的坐标;(3)、当点在线段上运动时,直线与抛物线在第一象限内交于点 , 则线段是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.