山西省晋中市平遥县2022年九年级5月质检(二模)数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 下列四个实数中,最大的数是( )A、-3 B、-1 C、 D、42. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )A、

B、
B、
C、
C、
D、
D、
4. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的身高情况 C、调查春节联欢晚会的收视率 D、调查济宁市居民日平均用水量5. 在数学探究课上,小明在探究圆周角和圆心角之间的数量关系时,按照圆周角与圆心的不同位置关系作出了如下图所示三个图进行探究小明的上述探究.过程体现的数学思想是( )
4. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的身高情况 C、调查春节联欢晚会的收视率 D、调查济宁市居民日平均用水量5. 在数学探究课上,小明在探究圆周角和圆心角之间的数量关系时,按照圆周角与圆心的不同位置关系作出了如下图所示三个图进行探究小明的上述探究.过程体现的数学思想是( )

 A、公理化思想 B、分类讨论思想 C、转化思想 D、建模思想6. 如图,在 中, , , , ,连接BC,CD,则 的度数是( )
A、公理化思想 B、分类讨论思想 C、转化思想 D、建模思想6. 如图,在 中, , , , ,连接BC,CD,则 的度数是( )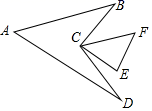 A、45° B、50° C、55° D、80°7. 不等式组 中两个不等式的解集在数轴上表示正确的是( )A、
A、45° B、50° C、55° D、80°7. 不等式组 中两个不等式的解集在数轴上表示正确的是( )A、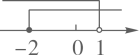 B、
B、 C、
C、 D、
D、 8. 公元263年,我国数学家利用“割圆术”计算圆周率.割圆术的基本思想是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”.随后,公元480年左右,我国另一位数学家又进一步得到圆周率精确到小数点后7位,由此可知,这两位数学家依次为( )A、刘徽,祖冲之 B、祖冲之,刘徽 C、杨辉,祖冲之 D、秦九韶,杨辉9. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、
8. 公元263年,我国数学家利用“割圆术”计算圆周率.割圆术的基本思想是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”.随后,公元480年左右,我国另一位数学家又进一步得到圆周率精确到小数点后7位,由此可知,这两位数学家依次为( )A、刘徽,祖冲之 B、祖冲之,刘徽 C、杨辉,祖冲之 D、秦九韶,杨辉9. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、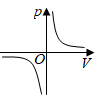 B、
B、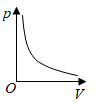 C、
C、 D、
D、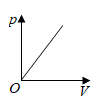 10. 如图,在 中, , , ,以点A为圆心,AC的长为半径画弧,交AB于点D , 交AC于点C , 以点B为圆心,AC的长为半径画弧,交AB于点E , 交BC于点F , 则图中阴影部分的面积为( )
10. 如图,在 中, , , ,以点A为圆心,AC的长为半径画弧,交AB于点D , 交AC于点C , 以点B为圆心,AC的长为半径画弧,交AB于点E , 交BC于点F , 则图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
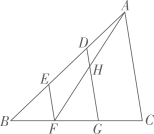
11. 化简: .12. 如图,在 中,D,E为边 的三等分点, ,H为 与 的交点.若 ,则 .
 13. 如图所示,电路连接完好,且各元件工作正常随机闭合开关 , , 中的两个,能让两个小灯泡同时发光的概率是 .
13. 如图所示,电路连接完好,且各元件工作正常随机闭合开关 , , 中的两个,能让两个小灯泡同时发光的概率是 .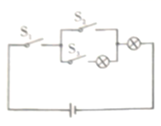 14. 如图,正方形 的边长为4, 的半径为1.若 在正方形 内平移( 可以与该正方形的边相切),则点A到 上的点的距离的最大值为.
14. 如图,正方形 的边长为4, 的半径为1.若 在正方形 内平移( 可以与该正方形的边相切),则点A到 上的点的距离的最大值为.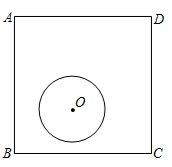 15. 如图,矩形纸片ABCD,AB=6cm,BC=8cm,E为边CD上一点.将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN=cm.
15. 如图,矩形纸片ABCD,AB=6cm,BC=8cm,E为边CD上一点.将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN=cm.
三、解答题
-
16. 计算:(1)、分解因式:(2)、以下是圆圆同学解方程的解答过程.
解:去分母,得: .
去括号,得: .
移项,合并同类项,
解得: .
请你分析上面圆圆同学的解答过程是否有错误?如果有错误,写出错误原因以及正确的解答过程.
17. 如图,在矩形ABCD中,点E在边BC上,点F在BC的延长线上,且 .求证:
 (1)、 ;(2)、四边形AEFD是平行四边形.18. 某地响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展“美化绿色城市”活动,绿化升级改造了总面积为360万平方米的区域.实际施工中,由于采用了新技术,实际平均每年绿化升级改造的面积是原计划平均每年绿化升级改造的面积的2倍,所以比原计划提前4年完成了上述绿化升级改造任务.实际平均每年绿化升级改造的面积是多少万平方米?19. 吸食毒品极易上瘾,不但对人的健康危害极大,而且严重影响家庭和社会的稳定,为了解同学们对禁毒知识的掌握情况,某校组织了“禁毒防毒”知识竞赛,将成绩分为:A(优秀)、B(良好)、C(合格)、D(不合格)四个等级,小李随机调查了部分同学的竞赛成绩,绘制了如下统计图.
(1)、 ;(2)、四边形AEFD是平行四边形.18. 某地响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展“美化绿色城市”活动,绿化升级改造了总面积为360万平方米的区域.实际施工中,由于采用了新技术,实际平均每年绿化升级改造的面积是原计划平均每年绿化升级改造的面积的2倍,所以比原计划提前4年完成了上述绿化升级改造任务.实际平均每年绿化升级改造的面积是多少万平方米?19. 吸食毒品极易上瘾,不但对人的健康危害极大,而且严重影响家庭和社会的稳定,为了解同学们对禁毒知识的掌握情况,某校组织了“禁毒防毒”知识竞赛,将成绩分为:A(优秀)、B(良好)、C(合格)、D(不合格)四个等级,小李随机调查了部分同学的竞赛成绩,绘制了如下统计图. (1)、本次抽样调查的学生人数是 ▲ , 请补全条形统计图;(2)、学校准备针对毒品危害分别举行一次专题培训和一次实践活动,并分别随机抽一位竞赛成绩不合格的同学参与发言,请用树状图或列表法求出恰好两次活动抽中同一人发言的概率;(3)、该校共有2000名学生,请你估计该校本次竞赛中成绩达到合格的学生人数.20. 如图,“五一”休假李明观察到一古城楼上方有一旗杆 , 已经测得古城楼高为 , 李明想测量旗杆的高度,于是在处观测得旗杆顶部的仰角为 , 观测得旗杆底部的仰角为 , 求旗杆的高度.(结果保留一位小数.参考数据: , , , )
(1)、本次抽样调查的学生人数是 ▲ , 请补全条形统计图;(2)、学校准备针对毒品危害分别举行一次专题培训和一次实践活动,并分别随机抽一位竞赛成绩不合格的同学参与发言,请用树状图或列表法求出恰好两次活动抽中同一人发言的概率;(3)、该校共有2000名学生,请你估计该校本次竞赛中成绩达到合格的学生人数.20. 如图,“五一”休假李明观察到一古城楼上方有一旗杆 , 已经测得古城楼高为 , 李明想测量旗杆的高度,于是在处观测得旗杆顶部的仰角为 , 观测得旗杆底部的仰角为 , 求旗杆的高度.(结果保留一位小数.参考数据: , , , )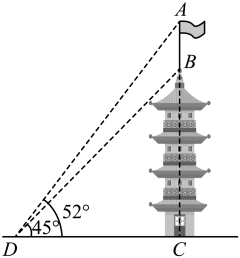 21. 阅读与思考:下面是某次数学课堂教学中的操作活动,请仔细阅读,并完成相应的任务.
21. 阅读与思考:下面是某次数学课堂教学中的操作活动,请仔细阅读,并完成相应的任务.小专题“图形的剪拼”
今天我们研究特殊四边形的时候发现,如果将其沿对角线裁剪后,得到的四个三角形可以拼成很多新的图形.我们设计做以下一些尝试.
图1是一张边长为2的正方形纸片,将其沿对角线剪开,得到图2所示四个全等的等腰直角三角形.用这四张纸片,重新摆放,可以得到特殊的图形.
操作一:奋进组接如图3所示的方式摆放,得到正方形 .
操作二:智慧组按如图4所示的方式摆放,得到正方形 .
操作三:如图5,将菱形沿对角线剪开,得到四个全等的直角三角形,无缝隙、不重叠地拼成一个矩形.




 (1)、任务一:如图3,正方形的边长为;(2)、任务二:如图4,若延长交于点 , 且 , 求正方形的面积;(3)、任务三:
(1)、任务一:如图3,正方形的边长为;(2)、任务二:如图4,若延长交于点 , 且 , 求正方形的面积;(3)、任务三:①请你用图5所得到的四个全等三角形无缝隙不重叠地拼出一个矩形;
②在菱形中,若 , . 在①中,你拼成的矩形的对角线长为 ▲ .
22. 问题情境:在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片沿对角线剪开,得和 . (1)、操作发现:将图1中的以点为旋转中心,按逆时针方向旋转 , 使 , 得到如图2所示的 , 分别延长和交于点 , 则四边形的形状是;(2)、创新小组将图1中的以点为旋转中心,按逆时针方向旋转 , 使 , 得到如图3所示的 , 连接、 , 得到四边形 , 发现它是矩形.请你证明这个结论.(3)、实践探究:缜密小组在创新小组发现结论的基础上,量得图3中 , , 然后提出一个问题:将沿着射线方向平移 , 得到 , 连接、 , 使四边形恰好为正方形,请你探究并直接写出所有的值.23. 已知抛物线与轴交于点、(点在点的左侧),与轴交于点 .
(1)、操作发现:将图1中的以点为旋转中心,按逆时针方向旋转 , 使 , 得到如图2所示的 , 分别延长和交于点 , 则四边形的形状是;(2)、创新小组将图1中的以点为旋转中心,按逆时针方向旋转 , 使 , 得到如图3所示的 , 连接、 , 得到四边形 , 发现它是矩形.请你证明这个结论.(3)、实践探究:缜密小组在创新小组发现结论的基础上,量得图3中 , , 然后提出一个问题:将沿着射线方向平移 , 得到 , 连接、 , 使四边形恰好为正方形,请你探究并直接写出所有的值.23. 已知抛物线与轴交于点、(点在点的左侧),与轴交于点 .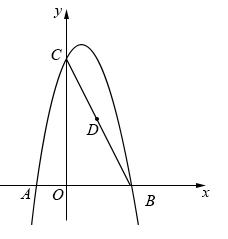
 (1)、求点、的坐标;(2)、连接 , 若的中点为点 , 请你求经过点和点的直线表达式;(3)、设点与点关于该抛物线的对称轴对称.在轴上是否存在点 , 使与相似,若存在,求出所有点坐标;若不存在,请说明理由.
(1)、求点、的坐标;(2)、连接 , 若的中点为点 , 请你求经过点和点的直线表达式;(3)、设点与点关于该抛物线的对称轴对称.在轴上是否存在点 , 使与相似,若存在,求出所有点坐标;若不存在,请说明理由.