山西省大同市2022年中考模拟测试（二）数学试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. -7的倒数是（）

A、 $- \frac{1}{7}$ B、 $\frac{1}{7}$ C、-7 D、7

查看试题解析
2. 2022年4月26日上午，大同市召开了2021年房地产经济指标新闻发布会，2021年大同市房地产市场呈现出“销量增加、价格稳定、稳中向好”的特点，全市房地产投资完成266.2亿元，同比增长44.5%，占全省房地产投资比重的13.7%，增速位列全省第二．把数据266.2亿元用科学记数法表示为（）

A、0.2662×10¹²元 B、2.662×10¹⁰元 C、2.662×10¹¹元 D、26.62×10⁹元

查看试题解析
3. 下列计算正确的是（）

A、x⁵-x³＝x² B、（x+2）²＝x²+4 C、（-2x²）³＝-8x⁵ D、（3x²y）÷（3xy）＝x

查看试题解析
4. 学校组织才艺表演比赛，前5名获奖．有11位同学参加比赛且他们所得的分数互不相同．某同学知道自己的比赛分数后，要判断自己能否获奖，在这11名同学成绩的统计量中只需知道一个量，它是（）

A、众数 B、方差 C、中位数 D、平均数

查看试题解析
5. 如图所示是由5个完全相同的小正方体搭成的几何体，如果将小正方体B放到小正方体A的正上方，则它的（）

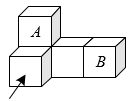A、左视图会发生改变，其他视图不变 B、俯视图会发生改变，其他视图不变 C、主视图会发生改变，其他视图不变 D、三种视图都会发生改变

查看试题解析
6. 数形结合是数学解题中常用的思想方法，使用数形结合的方法，很多问题可迎刃而解，且解法简洁．如图，直线y＝3x和直线y＝ax+b交于点（1，3），根据图象分析，方程3x＝ax+b的解为（）

A、x＝1 B、x＝-1 C、x＝3 D、x＝-3

查看试题解析
7. 不等式3（1-x）＞2-4x的解在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
8. 把函数 $y = x^{2} - 2 x + 3$ 的图象向左平移1个单位长度，平移后图象的函数解析式为（）

A、 $y = x^{2} + 2$ B、 $y = (x - 1)^{2} + 1$ C、 $y = {(x - 2)}^{2} + 2$ D、 $y = (x - 1)^{2} - 3$

查看试题解析
9. 如图，AB是 $⊙ O$ 的直径，点C在 $⊙ O$ 上，连接AC、BC，过点O作 $O D ∥ A C$ 交 $⊙ O$ 于点D，点C、D在AB的异侧．若 $∠ B = 24 °$ ，则 $∠ B C D$ 的度数是（）

A、66° B、67° C、57° D、48°

查看试题解析
10. 山西传统工艺源远流长，种类丰富，其中“高平珐华器、平遥推光漆和新绛澄泥砚”因其高超的制作工艺、独特的文化内涵、重要的艺术价值，被誉为“山西三宝”．图1是平遥推光漆器的一种图案，图2是选取其某部分并且放大后的示意图，四边形ABCD是边长为2的正方形，分别以正方形的四个顶点为圆心，对角线的长的一半为半径在正方形内画弧，四条弧相交于点O．则图中阴影部分的面积为（）

A、 $\frac{1}{4} π$ B、 $π - 2$ C、 $2 π$ D、 $2 π - 4$

查看试题解析

二、填空题

11. 计算： $2 \sqrt{27} - 3 \sqrt{3} =$ ．

查看试题解析
12. 如图，用同样规格的黑白两种颜色的正方形瓷砖，按下图的方式铺地板，则第n个图形中有黑色瓷砖块．

查看试题解析
13. 如图，四边形ABCD是菱形，∠ACD=30°，BD=6，则AB= ．

查看试题解析
14. 由于新能源汽车越来越多，为了解决充电难的问题，现对一面积为 $12000 m^{2}$ 的矩形停车场进行改造.将该矩形停车场的长减少20m，减少的这部分区域用于修建电动汽车充电桩，原停车场的剩余部分就变成了正方形，则原停车场的长是.

查看试题解析
15. 如图，在△ABC中， $A B = A C = 10$ ， $B C = 12$ ， D是AB的中点，过点A作 $A F ⊥ B C$ 于F，过点D作 $D E ⊥ A C$ 于E，AF与DE交于点G，则DG的长为．

查看试题解析

三、解答题

16.

(1)、计算： $| 2 - \sqrt{3} | + 202 2^{0} - {(\frac{1}{2})}^{- 1} + t a n 6 0^{°}$

(2)、下面是小亮同学进行分式化简的过程，请认真阅读并完成相应任务．
$(\frac{3 x}{x - 2} - \frac{x}{x + 2}) \cdot \frac{x^{2} - 4}{x}$
$= \frac{3 x}{x - 2} \cdot \frac{x^{2} - 4}{x} - \frac{x}{x + 2} \cdot \frac{x^{2} - 4}{x} . . .$ 第一步
$= \frac{3 x}{x - 2} \cdot \frac{(x + 2) (x - 2)}{x} - \frac{x}{x + 2} \cdot \frac{(x + 2) (x - 2)}{x} \cdot \cdot \cdot$ 第二步
$= 3 (x + 2) - (x - 2) ⋯$ 第三步
$= 3 x + 6 - x - 2 ⋯$ 第四步
$= 2 x + 4 ⋯$ 第五步
任务一：填空：
①以上化简步骤中，第一步是依据      ▲ （填运算律）进行变形的；
②第三步是进行分式的约分，约分的依据是      ▲ ；
③第      ▲ 步开始出现错误，这一步错误的原因是      ▲ ；
任务二：请直接写出该分式化简后的正确结果．

查看试题解析
17. 如图，在矩形ABCD中，点E、F分别是边AB、CD的中点．求证：DE=BF．

查看试题解析
18. 如图，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图象分别与x轴，y轴交于C，D两点，与反比例函数 $y_{2} = \frac{m}{x} (m \neq 0)$ 的图象交于A（2，3），B（6，n）两点．

(1)、求一次函数与反比例函数的表达式；

(2)、观察图像，当x>0时，请直接写出 $\frac{m}{x} > k x + b$ 的解集．

查看试题解析
19. “校园安全”越来越受到人们的关注，近日市教育局印发了《学校日常安全教育基本内容》的通知，某中学就学生对安全教育基本内容的了解程度，随机调查了本校的部分学生．根据调查统计后，绘制成如图所示的统计图．
请根据图中信息，解答下列问题：

(1)、本次抽取调查的学生共有人，其中“了解较多”的占%；

(2)、请补全条形统计图；

(3)、若该校共有1000名学生，根据上述调查，估计此校对安全教育基本内容“非常了解”和“了解较多”的学生共有人；

(4)、“校园安全无小事，安全知识学起来”．某校宣传小组为了进一步宣传学习《学校日常安全教育基本内容》，收集到如下相应的图片，将其制成卡片（除内容外，其余完全相同，将防溺水安全、交通安全、消防安全、食品安全图片分别记为A，B，C，D）．他们将这四张卡片背面朝上，洗匀放好，从中随机抽取一张，不放回，再从中随机抽取一张，请用列表或画树状图的方法，求抽到的两张卡片恰好是A（防溺水安全）和C（消防安全）的概率．

查看试题解析

20. 阅读与思考

下面是某数学兴趣小组探究过直线外一点作已知直线的平行线的方法，请仔细阅读，并完成相应的任务．

已知：直线l和直线l外一点P（如图1）

求作：l的平行线，使它经过点P．

作法1：如图2，①在直线l上任取一点B，作射线BP；

②以B为圆心，BP长为半径画弧，交直线l于点C；

③分别以点P，C为圆心，大于 $\frac{1}{2} P C$ 的长为半径画弧，两弧相交于D，作射线BD；

④以点P为圆心，PB长为半径画弧，交射线BD于点E；

⑤作直线PE，直线PE即为所求．

作法2：如图3，①在直线l上任取一点A，作直线PA；

②分别以点A和点P为圆心，大于 $\frac{1}{2} A P$ 的长为半径画弧，两弧相交于B，C两点；

③作直线BC，交AP于点O，交直线l于点D；

④在射线OB上截取 $O E = O D$ ；

⑤作直线PE，则直线PE就是所求作的平行线．

任务：

(1)、下面是作法1的证明过程，请将空缺的依据补充完整．

证明：由作图可知， $P B = P E$

∴∠PBE=∠PEB（依据1：）

由作图知，BD是∠PBC的平分线，

∴ $∠ P B E = ∠ E B C$

∴ $∠ P E B = ∠ E B C$

∴PE//l（依据2：）

(2)、根据作法2的作图过程，证明PE//l；

(3)、请你用与上述两种作法不同的方法，在图4中用尺规过点P作已知直线l的平行线（保留作图痕迹，不写作法）．

查看试题解析

21. 随着5G时代的到来，我们“想象”的生活开始变为现实．某移动通讯公司为了提升5G网络信号，在山坡AD上加装了5G信号塔PQ（如图所示），信号塔底端Q到水平地面的铅直高度QG为1.5米．为了提醒市民，在距离G点9米的水平地面上立了一块警示牌MN，当太阳光线与水平线所成的夹角为53°时，信号塔顶端P的影子落在警示牌上的点E处，且EN长为3米．

(1)、求信号塔PQ的高度（结果精确到0.1米．参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）

(2)、极高的网速，让下载不再等待.5G手机的下载速度很快，比4G下载速度每秒多95MB，下载一部1000MB的电影，5G比4G要快190秒，求5G手机的下载速度．

查看试题解析
22. 综合与实践
问题情境：
将两个完全相同的等腰Rt△ABC和等腰Rt△CDE按图1方式放置，∠ACB=∠DCE=90°，将Rt△CDE绕点C顺时针旋转，连接AE，BD，AE与BD相交于点G．
猜想证明：

(1)、在图1中，请判断AE与BD的数量关系与位置关系，并说明理由；

(2)、当旋转到CE//AB时，如图2，证明：AE平分∠BAC；

(3)、若旋转到如图3所示的位置时，连接BE、此时△BCE恰好是等边三角形，AE与BC相交于点F，请你直接写出 $\frac{B F}{C F}$ 的值．

查看试题解析
23. 综合与探究
如图，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 与x轴交于点 $A (- 1 ， 0)$ 和点 $B (4 ， 0)$ ，与y轴交于点C，连接BC．

(1)、求抛物线的表达式及点C的坐标；

(2)、点P是抛物线对称轴上一点，点Q为平面内一点，当以点B、C、P、Q为顶点的四边形是以BC为边的矩形时，请直接写出点P的坐标；

(3)、点D是第四象限内抛物线上一动点，当∠BCD=2∠ABC时，求点D的坐标．

查看试题解析