山西吕梁孝义市2022年九年级中考第三次模拟数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. -2的相反数为( )A、-2 B、2 C、±2 D、2. 如图,直线a,b被直线c所截,且 , , 则等于( )
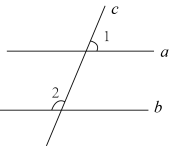 A、55° B、65° C、125° D、135°3. 一季度,面对国际环境更趋复杂严峻和国内疫情频发带来的多重考验,在以习近平同志为核心的党中央坚强领导下,科学统筹疫情防控和经济社会发展,初步核算,一季度国内生产总值约为27万亿元,按不变价格计算,同比增长4.8%.数据27万亿元用科学记数法表示为( )A、元 B、元 C、元 D、元4. 如图是一个正方体的表面展开图,在原正方体中,与“诚”字所在面相对的面上的汉字是( )
A、55° B、65° C、125° D、135°3. 一季度,面对国际环境更趋复杂严峻和国内疫情频发带来的多重考验,在以习近平同志为核心的党中央坚强领导下,科学统筹疫情防控和经济社会发展,初步核算,一季度国内生产总值约为27万亿元,按不变价格计算,同比增长4.8%.数据27万亿元用科学记数法表示为( )A、元 B、元 C、元 D、元4. 如图是一个正方体的表面展开图,在原正方体中,与“诚”字所在面相对的面上的汉字是( ) A、守 B、信 C、担 D、当5. 为了防控疫情,各级防控部门积极推广疫苗接种工作,某市某接种点1-5月接种人数如下表,则这组数据的中位数和众数分别是( )
A、守 B、信 C、担 D、当5. 为了防控疫情,各级防控部门积极推广疫苗接种工作,某市某接种点1-5月接种人数如下表,则这组数据的中位数和众数分别是( )月份
1
2
3
4
5
接种人数(万人)
1.2
1.8
1.6
2.1
1.8
A、1.2万人,1.6万人 B、1.6万人,1.8万人 C、1.8万人,1.8万人 D、1.8万人,2.1万人6. 一元二次方程的根为( )A、 , B、 , C、 , D、 ,7. 公元前6世纪古希腊的毕达哥拉斯学派认为“万物皆数”,意思是一切量都可以用整数或整数的比(分数)表示.后来,这一学派的希帕索斯发现,边长为1的正方形的对角线的长度不能用整数或整数的比表示,由此引发了第一次数学危机.这里“不能用整数或整数的比表示的数”是指( ) A、有理数 B、无理数 C、质数 D、实数8. 如图是反比例函数的图象,当时,y的取值范围是( )
A、有理数 B、无理数 C、质数 D、实数8. 如图是反比例函数的图象,当时,y的取值范围是( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,点C,D分别是 , 的中点,点A的坐标为 , 点D的坐标为 , 则点C的坐标为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,点C,D分别是 , 的中点,点A的坐标为 , 点D的坐标为 , 则点C的坐标为( ) A、 B、 C、 D、10. 如图,A,B,C三点均在⊙O上,∠A+∠C=100°,则∠O等于( )
A、 B、 C、 D、10. 如图,A,B,C三点均在⊙O上,∠A+∠C=100°,则∠O等于( ) A、160° B、140° C、100° D、80°
A、160° B、140° C、100° D、80°二、填空题
-
11. 函数 中,自变量x的取值范围是 .12. 如图,是的切线, , 交圆O于点C,若 , 则扇形的面积为 .
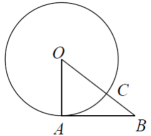 13. 2022年5月30日是第六个全国科技工作者日,主题为“创新争先,自立自强”.为了庆祝第六个全国科技工作者日,某学校准备举办科技知识竞赛活动,班需要从甲,乙两位同学中选拔一位同学参加学校举办的此次活动,甲、乙两位同学的5次选拔成绩如统计图所示,两位同学的平均成绩相等,从他们的稳定性考虑,应该选择的同学是 .
13. 2022年5月30日是第六个全国科技工作者日,主题为“创新争先,自立自强”.为了庆祝第六个全国科技工作者日,某学校准备举办科技知识竞赛活动,班需要从甲,乙两位同学中选拔一位同学参加学校举办的此次活动,甲、乙两位同学的5次选拔成绩如统计图所示,两位同学的平均成绩相等,从他们的稳定性考虑,应该选择的同学是 .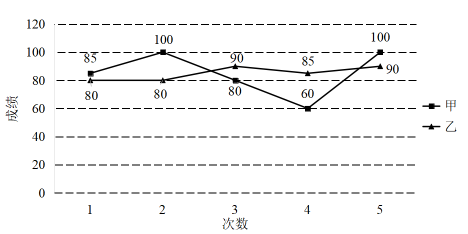 14. 超市用1200元钱批发了A,B两种西瓜进行销售,两种西瓜的批发价和零售价如下表所示,若计划将这批西瓜全部售完后,所获利润率不低于40%,则该超市至少批发A种西瓜 .
14. 超市用1200元钱批发了A,B两种西瓜进行销售,两种西瓜的批发价和零售价如下表所示,若计划将这批西瓜全部售完后,所获利润率不低于40%,则该超市至少批发A种西瓜 .名称
A
B
批发价(元/)
4
3
零售价(元/)
6
4
15. 如图,将矩形绕点C顺时针旋转,使点B的对应点E落在上时,得到矩形 , 若 , , 则的面积为 .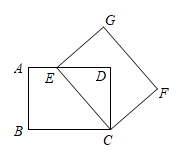
三、解答题
-
16.(1)、(2)、解方程:17. 初中阶段有五种基本尺规作图,分别是:①作一条线段等于已知线段;②作一个角等于已知角;③作一个角的平分线;④作一条线段的垂直平分线;⑤过一点作已知直线的垂线.
数学课上,老师出示了如下题目:如图1,已知线段m,n.运用尺规作图画出 , 使斜边 , 一条直角边 .
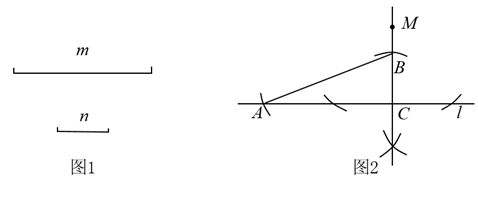 (1)、如图2是小亮所作的 , 并保留了作图痕迹.小亮的作图过程用到的基本作图有;(填序号)(2)、请你用一种与小亮不同的尺规作图方法再作一个 , 使满足上述条件.(不写作法,但保留作图痕迹)18. 2022年3月23日15:40,“天宫课堂”第二课开讲,本次太空授课活动同样采取天地对话方式进行,在约45分钟的授课中,神舟十三号飞行乘组生动演示了微重力环境下太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验.某校组织全体学生观看了本次授课活动,并让同学们选出自己最感兴趣的实验.学校教务处随机抽取了部分学生对授课活动最感兴趣的实验进行了问卷调查,具体问卷如下:
(1)、如图2是小亮所作的 , 并保留了作图痕迹.小亮的作图过程用到的基本作图有;(填序号)(2)、请你用一种与小亮不同的尺规作图方法再作一个 , 使满足上述条件.(不写作法,但保留作图痕迹)18. 2022年3月23日15:40,“天宫课堂”第二课开讲,本次太空授课活动同样采取天地对话方式进行,在约45分钟的授课中,神舟十三号飞行乘组生动演示了微重力环境下太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验.某校组织全体学生观看了本次授课活动,并让同学们选出自己最感兴趣的实验.学校教务处随机抽取了部分学生对授课活动最感兴趣的实验进行了问卷调查,具体问卷如下:

将调查结果绘制成如下所示的条形统计图和扇形统计图(均不完整)

请根据统计图中提供的信息,解答下列问题:
(1)、参与本次问卷调查的总人数为人;在扇形统计图中,“太空抛物实验”的圆心角是度.(2)、请将条形统计图补充完整.(3)、若该校有3600名学生,请你估计选择太空“冰雪”实验的有多少人.(4)、为弘扬科学精神,传播航天知识、感悟榜样精神与力量,学校教务处决定开展“飞天梦永不失重,科学梦张力无限”的主题活动,包含了以下四个内容:A.书写观后感;B.演示科学实验;C.绘制手抄报;D.开展主题班会.王老师在四张完全相同的卡片上分别写了A,B,C,D,然后背面朝上放置,搅匀后要求先由七年级派一名代表从中随机抽取一张,记下标号后放回,再由八年级派一名代表从中随机抽取一张,请用列表或画树状图的方法,求两个年级代表抽到的主题卡片中有演示科学实验(B)的概率.
19. 近年来,吕梁市坚持经济转型发展的强劲态势,在新能源方面,充分挖掘吕梁山脉的风力资源和日照资源优势,加快推进风力发电、光伏发电发展.2020年吕梁市风力发电与光伏发电合计发电量为28亿度,2021年风力发电与光伏发电合计发电量34亿度,已知2021年风力发电量是2020年的1.1倍,2021年光伏发电量是2020年的1.5倍.
 (1)、求吕梁市2020年风力发电与光伏发电量分别是多少亿度?(2)、风力发电机组俗称“大风车”,某基地现有A,B型大风车15台,其中A型大风车a台,且B型大风车的数量不低于A型大风车的2倍,每台A型大风车每年发电量为200万度,每台B型大风车每年发电量为350万度,若这15台大风车每年发电量为w万度,请你求出w关于a的函数关系式,并求出w的最小值.20. 如图1是工人用升降机维修路灯的实物图,图2是升降机工作示意图.学习兴趣小组计划通过此示意图计算路灯的高度.他们通过测量和咨询工人师傅了解到如下信息:路灯垂直于地面,机械臂米,米,路灯顶部到工作台的距离米,车厢上部到地面距离为米, , . 根据上述信息,请你求出路灯的高度.(结果精确到米.参考数值: , , , )
(1)、求吕梁市2020年风力发电与光伏发电量分别是多少亿度?(2)、风力发电机组俗称“大风车”,某基地现有A,B型大风车15台,其中A型大风车a台,且B型大风车的数量不低于A型大风车的2倍,每台A型大风车每年发电量为200万度,每台B型大风车每年发电量为350万度,若这15台大风车每年发电量为w万度,请你求出w关于a的函数关系式,并求出w的最小值.20. 如图1是工人用升降机维修路灯的实物图,图2是升降机工作示意图.学习兴趣小组计划通过此示意图计算路灯的高度.他们通过测量和咨询工人师傅了解到如下信息:路灯垂直于地面,机械臂米,米,路灯顶部到工作台的距离米,车厢上部到地面距离为米, , . 根据上述信息,请你求出路灯的高度.(结果精确到米.参考数值: , , , ) 21. 阅读下列材料,并完成相应学习任务:
21. 阅读下列材料,并完成相应学习任务:勾股定理,是指直角三角形的两条直角边的平方和等于斜边的平方.在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派.
中国古代称直角三角形为勾股形(直角边中较小者为勾,另一长直角边为股,斜边为弦),周朝时期的商高提出了“勾三股四弦五”的特例,所以我国称这个定理为勾股定理,也有人称商高定理.
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。下面是小明搜集到的勾股定理的一种证明方法(不完整).
如图,在中, , , , .
求证: .
证明:作出的外接圆O.延长到点D,使得 . 连接 , 交于点E.延长与的延长线交于点M.连接 , 延长与交于点N
∵ , ∴ , 为的直径.
∴ . (依据1)
∴ ,
…

学习任务:
(1)、材料中“依据1”是:;(2)、请根据上述材料中的部分证明过程,判断与的数量关系和位置关系,并证明;(3)、请结合材料与(2)中的证明过程,用不同的方法表示图中阴影部分面积,完成勾股定理的证明(用含a,b,c的式子表示).22. 综合与实践:数学活动课上,老师让同学们根据下面情境提出问题并解答.
问题情境:在中,点P是边上一点.将沿直线折叠,点D的对应点为E.
“兴趣小组”提出的问题是:如图1,若点P与点A重合,过点E作 , 与交于点F,连接 , 则四边形是菱形.
 (1)、数学思考:请你证明“兴趣小组”提出的问题;(2)、拓展探究:“智慧小组”提出的问题是:如图2,当点P为的中点时,延长交于点F,连接 . 试判断与的位置关系,并说明理由.
(1)、数学思考:请你证明“兴趣小组”提出的问题;(2)、拓展探究:“智慧小组”提出的问题是:如图2,当点P为的中点时,延长交于点F,连接 . 试判断与的位置关系,并说明理由.请你帮助他们解决此问题.
(3)、问题解决:“创新小组”在前两个小组的启发下,提出的问题是:如图3,当点E恰好落在边上时, , , . 则的长为 . (直接写出结果)23. 综合与探究如图,抛物线与x轴交于A,B两点,与y轴交于点C.点M是y轴右侧抛物线上一动点,过点M作的平行线,交直线于点D,交x轴于点E.
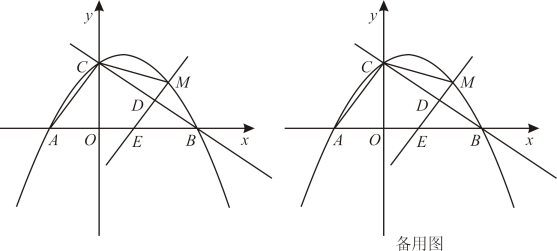 (1)、请直接写出点A,B,C的坐标及直线的解析式;(2)、当时,求点D的坐标;(3)、试探究在点M运动的过程中,是否存在以点A,C,E,M,为顶点的四边形是平行四边形?若存在,直接写出M的坐标,若不存在说明理由.
(1)、请直接写出点A,B,C的坐标及直线的解析式;(2)、当时,求点D的坐标;(3)、试探究在点M运动的过程中,是否存在以点A,C,E,M,为顶点的四边形是平行四边形?若存在,直接写出M的坐标,若不存在说明理由.