河北省唐山市路南区2022年中考三模数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 在平面内与点的距离为1cm的点的个数为( )A、无数个 B、3个 C、2个 D、1个2. 与互为倒数的是( )A、 B、 C、 D、3. 如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
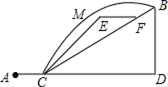 A、A→C→D→B B、A→C→F→B C、A→C→E→F→B D、A→C→M→B4. 运算后结果正确的是( )A、 B、 C、 D、5. 如图,天平右盘中的每个砝码的质量都是1克,则物体A的质量m克的取值范围表示在数轴上为( )
A、A→C→D→B B、A→C→F→B C、A→C→E→F→B D、A→C→M→B4. 运算后结果正确的是( )A、 B、 C、 D、5. 如图,天平右盘中的每个砝码的质量都是1克,则物体A的质量m克的取值范围表示在数轴上为( ) A、
A、 B、
B、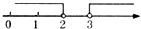 C、
C、 D、
D、 6. 一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M、N.那么∠CME+∠BNF是( )
6. 一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M、N.那么∠CME+∠BNF是( )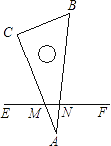 A、150° B、180° C、135° D、不能确定7. 下列计算正确的是( )A、 B、 C、 D、8. 如图,要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下:
A、150° B、180° C、135° D、不能确定7. 下列计算正确的是( )A、 B、 C、 D、8. 如图,要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下: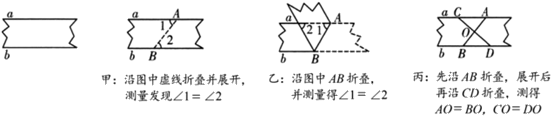
下列判断正确的是( )
A、甲、乙能得到 , 丙不能 B、甲、丙能得到 , 乙不能 C、乙、丙能得到 , 甲不能 D、甲、乙、丙均能得到9. 如图1,点 , , 是数轴上从左到右排列的三个点,分别对应的数为-5,b,4,某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对应刻度1.8cm,点C对齐刻度5.4cm.则数轴上点B所对应的数b为( ) A、3 B、-1 C、-2 D、-310. 问题背景:如图,AD是的中线,四边形是平行四边形.讨论交流:
A、3 B、-1 C、-2 D、-310. 问题背景:如图,AD是的中线,四边形是平行四边形.讨论交流:小明说:“若 , 则四边形是矩形.”
小强说:“若 , 则四边形是菱形.”
下列说法中正确的是( )
 A、小明不对,小强对 B、小明对,小强不对 C、小明和小强都对 D、小明和小强都不对11. 在化简题中,◆表示+,-,×,÷四个运算符号中的某一个.当 , 时,的值为22,则◆所表示的符号为( )A、 B、 C、+ D、-12. 如图,在中,P、Q分别为AB、AC边上的点,且满足 . 根据以上信息,嘉嘉和淇淇给出了下列结论:
A、小明不对,小强对 B、小明对,小强不对 C、小明和小强都对 D、小明和小强都不对11. 在化简题中,◆表示+,-,×,÷四个运算符号中的某一个.当 , 时,的值为22,则◆所表示的符号为( )A、 B、 C、+ D、-12. 如图,在中,P、Q分别为AB、AC边上的点,且满足 . 根据以上信息,嘉嘉和淇淇给出了下列结论:嘉嘉说:连接PQ,则PQ//BC.
淇淇说: .
对于嘉嘉和淇淇的结论,下列判断正确的是( )
 A、嘉嘉符合题意,淇淇不符合题意 B、嘉嘉不符合题意,淇淇符合题意 C、两人都符合题意 D、两人都不符合题意13. 如图,将一个棱长为3的正方体表面涂上颜色,再把它分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,只有一个面被涂色的概率为( )
A、嘉嘉符合题意,淇淇不符合题意 B、嘉嘉不符合题意,淇淇符合题意 C、两人都符合题意 D、两人都不符合题意13. 如图,将一个棱长为3的正方体表面涂上颜色,再把它分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,只有一个面被涂色的概率为( ) A、 B、 C、 D、14. 如图,点O为的内心, , , 点M,N分别为 , 上的点,且 . 甲、乙、丙三人有如下判断:甲:;乙:四边形的面积为定值;丙:当时,的周长有最小值.则下列说法正确的是( )
A、 B、 C、 D、14. 如图,点O为的内心, , , 点M,N分别为 , 上的点,且 . 甲、乙、丙三人有如下判断:甲:;乙:四边形的面积为定值;丙:当时,的周长有最小值.则下列说法正确的是( ) A、只有甲正确 B、只有乙错误 C、乙、丙都正确 D、只有丙错误15. 如图,过y轴上任意一点P作x轴的平行线,分别与反比例函数和的图象交于A点和B点,若C为x轴上任意一点,连接AC、BC,则△ABC的面积为( )
A、只有甲正确 B、只有乙错误 C、乙、丙都正确 D、只有丙错误15. 如图,过y轴上任意一点P作x轴的平行线,分别与反比例函数和的图象交于A点和B点,若C为x轴上任意一点,连接AC、BC,则△ABC的面积为( ) A、3 B、4 C、5 D、816. 正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( )
A、3 B、4 C、5 D、816. 正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( )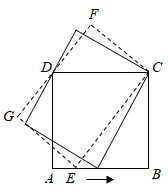 A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变
A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变二、填空题
-
17. 代数式化简的结果是 , 则整数 . 当时,(填“>”“<”“=”)18. 如图是一个长方体的主视图和左视图,其中左视图的面积是 . 则
 (1)、用x表示图中长方体的高为 .(2)、用x表示其俯视图的面积 .19. 如图,抛物线 , 直线与抛物线、轴分别相交于点、 .
(1)、用x表示图中长方体的高为 .(2)、用x表示其俯视图的面积 .19. 如图,抛物线 , 直线与抛物线、轴分别相交于点、 .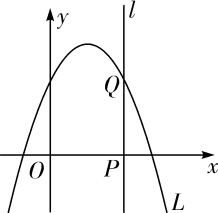 (1)、当时,点的坐标为;(2)、当时,在拋物线与轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,此时“可点”的个数为 .
(1)、当时,点的坐标为;(2)、当时,在拋物线与轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,此时“可点”的个数为 .三、解答题
-
20. 已知:△ABC的边长 , , , 且 .
 (1)、判断三角形的形状,并说明理由;(2)、若 , 求的三边长.21. 嘉琪记录了她连续两天陪妈妈去水果店买水果的账目:第一天买了2斤香蕉和1斤苹果,共花了11元,第二天买了1斤香蕉和3斤苹果,共花了43元.已知两天中,香蕉和苹果的单价相同.她的记录是否正确?若正确,请算出香蕉和苹果的单价,若错误,请说明理由.22. 今年疫情期间,为防止疫情扩散,人们见面的机会少了,但是随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷,为此,孙老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种)进行调查.将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、判断三角形的形状,并说明理由;(2)、若 , 求的三边长.21. 嘉琪记录了她连续两天陪妈妈去水果店买水果的账目:第一天买了2斤香蕉和1斤苹果,共花了11元,第二天买了1斤香蕉和3斤苹果,共花了43元.已知两天中,香蕉和苹果的单价相同.她的记录是否正确?若正确,请算出香蕉和苹果的单价,若错误,请说明理由.22. 今年疫情期间,为防止疫情扩散,人们见面的机会少了,但是随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷,为此,孙老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种)进行调查.将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: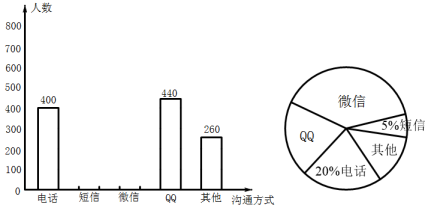 (1)、这次参与调查的共有人;在扇形统计图中,表示“微信”的扇形圆心角的度数为;其它沟通方式所占的百分比为 .(2)、将条形统计图补充完整;(3)、如果我国有13亿人在使用手机.
(1)、这次参与调查的共有人;在扇形统计图中,表示“微信”的扇形圆心角的度数为;其它沟通方式所占的百分比为 .(2)、将条形统计图补充完整;(3)、如果我国有13亿人在使用手机.①请估计最喜欢用“微信”进行沟通的人数;
②在全国使用手机的人中随机抽取一人,用频率估计概率,求抽取的恰好使用“QQ”的概率是多少?
23. 小明、小亮利用遥控器在电子屏上分别玩甲、乙两个小飞机,甲、乙两个小飞机分别从水平线起点和距水平线起点高15m处同时出发,匀速上升60min.如图是甲、乙两个小飞机所在位置的高度y(单位:m)与飞机上升时间x(单位:min)的函数图象.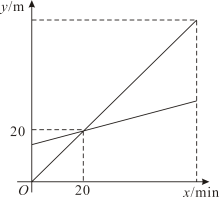 (1)、求这两个小飞机在上升过程中y关于x的函数解析式;(2)、当这两个小飞机的高度相差18m时,求上升的时间.24. 已知,在半圆中,直径 , 点 , 在半圆上运动,(点 , 可以与 , 两点重合),弦 .
(1)、求这两个小飞机在上升过程中y关于x的函数解析式;(2)、当这两个小飞机的高度相差18m时,求上升的时间.24. 已知,在半圆中,直径 , 点 , 在半圆上运动,(点 , 可以与 , 两点重合),弦 .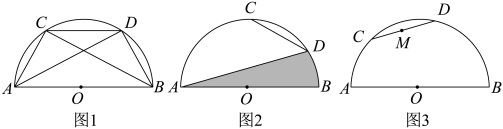 (1)、如图1,当时,直接写出图中标注顶点的所有全等三角形;(2)、如图2,若时,求图中阴影部分(弦AD、直径AB、弧BD围成的(图形)的面积;(3)、如图3,取CD的中点 , 点从点开始运动到点与点重合时结束,在整个运动过程中:
(1)、如图1,当时,直接写出图中标注顶点的所有全等三角形;(2)、如图2,若时,求图中阴影部分(弦AD、直径AB、弧BD围成的(图形)的面积;(3)、如图3,取CD的中点 , 点从点开始运动到点与点重合时结束,在整个运动过程中:①点M到AB的距离的最小值是;
②直接写出点M的运动路径长 .
25. 北京冬奥会的召开激起了人们对冰雪运动的极大热情,如图是某小型跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线近似表示滑雪场地上的一座小山坡,某滑雪爱好者小张从点O正上方A点滑出,滑出后沿一段抛物线运动.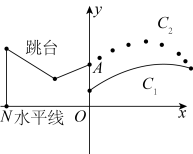 (1)、当小张滑到离A处的水平距离为6米时,其滑行高度最大,为米,则 .(2)、在(1)的条件下,当小张滑出后离A的水平距离为多少米时,他滑行高度与小山坡的竖直距离为米?(3)、小张若想滑行到最大高度时恰好在坡顶正上方,且与坡顶距离不低于3米,求跳台滑出点的最小高度.26. 如图,在▱ABCD中,BC=8, S▱ABCD=24 , tanA= , M是BC的中点,点P从点M出发沿MB以每秒1个单位长度的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长度的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作等边△EPQ,使它和▱ABCD在射线BC的同侧,点P,Q同时出发,点P返回到点M时终止运动,点Q也随之停止,设点P,Q运动时间是t秒(t>0).
(1)、当小张滑到离A处的水平距离为6米时,其滑行高度最大,为米,则 .(2)、在(1)的条件下,当小张滑出后离A的水平距离为多少米时,他滑行高度与小山坡的竖直距离为米?(3)、小张若想滑行到最大高度时恰好在坡顶正上方,且与坡顶距离不低于3米,求跳台滑出点的最小高度.26. 如图,在▱ABCD中,BC=8, S▱ABCD=24 , tanA= , M是BC的中点,点P从点M出发沿MB以每秒1个单位长度的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长度的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作等边△EPQ,使它和▱ABCD在射线BC的同侧,点P,Q同时出发,点P返回到点M时终止运动,点Q也随之停止,设点P,Q运动时间是t秒(t>0). (1)、①当t=1秒时,S△PQE=;②当t=秒时,点刚好落在边AD上;(2)、当PM=2时,求△EPQ与▱ABCD重叠部分面积;(3)、随着时间t的变化,△EPQ的外心是否一直在▱ABCD内部?如果在,请说明理由;如果不在,直接写出△EPQ的外心在▱ABCD内部时t的取值范围.
(1)、①当t=1秒时,S△PQE=;②当t=秒时,点刚好落在边AD上;(2)、当PM=2时,求△EPQ与▱ABCD重叠部分面积;(3)、随着时间t的变化,△EPQ的外心是否一直在▱ABCD内部?如果在,请说明理由;如果不在,直接写出△EPQ的外心在▱ABCD内部时t的取值范围.