河北省保定市易县2022年中考三模考试数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 如图,在平面内作已知直线m的垂线,可作垂线的条数有( )
 A、0条 B、1条 C、2条 D、无数条2. 若 为实数,则下列各式的运算结果比 小的是( )A、 B、 C、a×1 D、3. 下列四个正方体的展开图中,能折叠成如图所示的正方体的是( )
A、0条 B、1条 C、2条 D、无数条2. 若 为实数,则下列各式的运算结果比 小的是( )A、 B、 C、a×1 D、3. 下列四个正方体的展开图中,能折叠成如图所示的正方体的是( ) A、
A、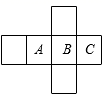 B、
B、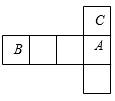 C、
C、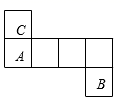 D、
D、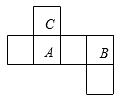 4. 下列各数中,与的和为有理数的是( )A、 B、 C、 D、5. 下列尺规作图,能确定 是 的中线的是( )A、
4. 下列各数中,与的和为有理数的是( )A、 B、 C、 D、5. 下列尺规作图,能确定 是 的中线的是( )A、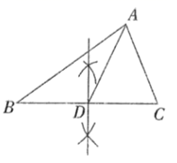 B、
B、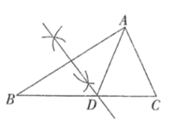 C、
C、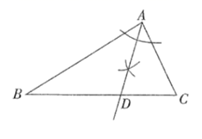 D、
D、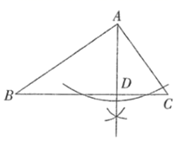 6. 如图,A是某公园的进口,B,C,D是三个不同的出口,小明从A处进入公园,那么在B,C,D三个出口中恰好从B出口出来的概率为( )
6. 如图,A是某公园的进口,B,C,D是三个不同的出口,小明从A处进入公园,那么在B,C,D三个出口中恰好从B出口出来的概率为( )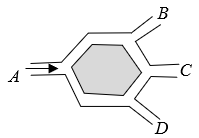 A、 B、 C、 D、7. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB长为( )
A、 B、 C、 D、7. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB长为( )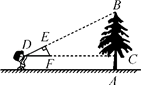 A、21.6m B、6.6m C、20.6m D、7.6m8. 如图,由一个正六边形和正五边形组成的图形中,的度数应是( )
A、21.6m B、6.6m C、20.6m D、7.6m8. 如图,由一个正六边形和正五边形组成的图形中,的度数应是( ) A、 B、 C、 D、9. 小华总结了以下结论,其中一定成立的是( )A、0不是单项式 B、多项式是二次三项式 C、“a与b的和的平方”表示为 D、“x的一半与y的2倍的差是非负数”表示为10. 如图,E,F,G为圆上的三点,∠FEG=50°,P点可能是圆心的是( ).A、
A、 B、 C、 D、9. 小华总结了以下结论,其中一定成立的是( )A、0不是单项式 B、多项式是二次三项式 C、“a与b的和的平方”表示为 D、“x的一半与y的2倍的差是非负数”表示为10. 如图,E,F,G为圆上的三点,∠FEG=50°,P点可能是圆心的是( ).A、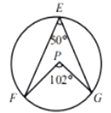 B、
B、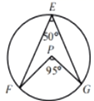 C、
C、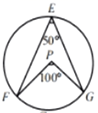 D、
D、 11. 在Rt△ABC中,∠C=90°,有一点D同时满足以下三个条件:①在直角边BC上;②在∠CAB的角平分线上;③在斜边AB的垂直平分线上,那么∠B为( )A、15° B、30° C、45° D、60°12. 一条直线 , 其中 , 那么该直线经过( )A、第二、四象限 B、第一、二、三象限 C、第一、三象限 D、第二、三、四象限13. 如图,正方形和正方形是位似图形,且点D与点G是一对对应点,点 , 点 , 则它们位似中心的坐标是( )
11. 在Rt△ABC中,∠C=90°,有一点D同时满足以下三个条件:①在直角边BC上;②在∠CAB的角平分线上;③在斜边AB的垂直平分线上,那么∠B为( )A、15° B、30° C、45° D、60°12. 一条直线 , 其中 , 那么该直线经过( )A、第二、四象限 B、第一、二、三象限 C、第一、三象限 D、第二、三、四象限13. 如图,正方形和正方形是位似图形,且点D与点G是一对对应点,点 , 点 , 则它们位似中心的坐标是( ) A、 B、 C、 D、14. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西方向的A处,若渔船沿北偏西方向以60海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东方向上,则B、C之间的距离为( )
A、 B、 C、 D、14. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西方向的A处,若渔船沿北偏西方向以60海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东方向上,则B、C之间的距离为( ) A、15海里 B、30海里 C、海里 D、海里15. 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A、15海里 B、30海里 C、海里 D、海里15. 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )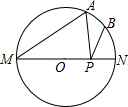 A、4 B、4 C、2 D、216. 把图1中周长为的长方形纸片分割成四张大小不等的正方形纸片A、B、C、D和一张长方形纸片E,并将它们按图2的方式放入周长为的的长方形中.设正方形C的边长为 , 正方形D的边长为 . 则下结论中正确的是( )
A、4 B、4 C、2 D、216. 把图1中周长为的长方形纸片分割成四张大小不等的正方形纸片A、B、C、D和一张长方形纸片E,并将它们按图2的方式放入周长为的的长方形中.设正方形C的边长为 , 正方形D的边长为 . 则下结论中正确的是( ) A、正方形C的边长为 B、正方形A的边长为 C、正方形B的边长为 D、阴影部分的周长为
A、正方形C的边长为 B、正方形A的边长为 C、正方形B的边长为 D、阴影部分的周长为二、填空题
-
17. 我们称使方程成立的一对数x,y为“相伴数对”,记为.(1)、若是“相伴数对”,则y的值为;(2)、若是“相伴数对”,请用含a的代数式表示b=.18. 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片沿过点A的直线折叠,使得点B落在上的点Q处.折痕为再将 , 分别沿折叠,此时点C,D落在上的同一点R处.请完成下列探究:
 (1)、∵ , ∴与位置关系为;(2)、线段与的数量关系为 .19. 如图,在平面直角坐标系中,为坐标原点,的边垂直轴于点 , 反比例函数的图像经过的中点 , 与边相交于点 , 若的坐标为 , .
(1)、∵ , ∴与位置关系为;(2)、线段与的数量关系为 .19. 如图,在平面直角坐标系中,为坐标原点,的边垂直轴于点 , 反比例函数的图像经过的中点 , 与边相交于点 , 若的坐标为 , . (1)、反比例函数的解析式是;(2)、设点是线段上的动点,过点且平行轴的直线与反比例函数的图象交于点 , 则面积的最大值是 .
(1)、反比例函数的解析式是;(2)、设点是线段上的动点,过点且平行轴的直线与反比例函数的图象交于点 , 则面积的最大值是 .三、解答题
-
20. 下面是小颖同学解一元二次方程的过程,请认真阅读并完成任务.
解:第一步
第二步
第三步
第四步
, 第五步
(1)、任务一:①小颖解方程的方法是;
②第二步变形的依据是;
(2)、任务二:请你用“公式法”解该方程.21. 如图,点D在等边的外部,E为边上的一点, , 交于点F, .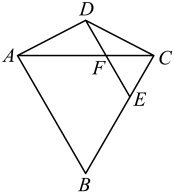 (1)、判断的形状,并说明理由;(2)、若 , , 求的长.22. 在一个不透明的盒子里,装有四个分别标有数字2、3、4、6的乒乓球,它们的形状、大小、颜色、质地完全相同,耀华同学先从盒子里随机取出一个小球,记为数字x,不放回,再由洁玲同学随机取出另一个小球,记为数字y,(1)、用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;(2)、求取出的坐标(x,y)对应的点落在反比例函数y= 图象上的概率.23. 已知中,都是锐角,且 ,(1)、分别求出三个内角度数;(2)、若 , 求长度.24. 在平面直角坐标系xOy中,已知点A(0,2),B(2,2),点M为线段AB上一点.
(1)、判断的形状,并说明理由;(2)、若 , , 求的长.22. 在一个不透明的盒子里,装有四个分别标有数字2、3、4、6的乒乓球,它们的形状、大小、颜色、质地完全相同,耀华同学先从盒子里随机取出一个小球,记为数字x,不放回,再由洁玲同学随机取出另一个小球,记为数字y,(1)、用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;(2)、求取出的坐标(x,y)对应的点落在反比例函数y= 图象上的概率.23. 已知中,都是锐角,且 ,(1)、分别求出三个内角度数;(2)、若 , 求长度.24. 在平面直角坐标系xOy中,已知点A(0,2),B(2,2),点M为线段AB上一点.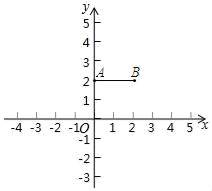 (1)、在点C(2,1),D(2,0),E(1,2)中,可以与点M关于直线y=x对称的点是;(2)、若x轴上存在点N,使得点N与点M关于直线y=x+b对称,求b的取值范围.(3)、过点O作直线l,若直线y=x上存在点N,使得点N与点M关于直线l对称(点M可以与点N重合),请你直接写出点N横坐标n的取值范围.25. 请阅读以下材料,并完成相应的任务
(1)、在点C(2,1),D(2,0),E(1,2)中,可以与点M关于直线y=x对称的点是;(2)、若x轴上存在点N,使得点N与点M关于直线y=x+b对称,求b的取值范围.(3)、过点O作直线l,若直线y=x上存在点N,使得点N与点M关于直线l对称(点M可以与点N重合),请你直接写出点N横坐标n的取值范围.25. 请阅读以下材料,并完成相应的任务【阅读材料】在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理,其中第二个引理是:
如图1,点P是弧的任意一点,于点C,点D在弦上且 , 在弧上取一点Q,使弧=弧 , 连接 , 则有.
 (1)、如图2,小明同学尝试说明“”,于是他连接了 , , , , 请根据小明的思路完成后续证明过程;(2)、如图3,以为直径的半圆上有一点P, , 直线l与相切于点P,过点于点E,交于点Q,求出的长.26. 在如图1所示的平面直角坐标系中,O为原点, ⊙C的圆心坐标为(−2,−2),半径为 , 直线y=−x+2与x轴,y轴分别交于点A,B,点P在线段AB上运动(包括端点).
(1)、如图2,小明同学尝试说明“”,于是他连接了 , , , , 请根据小明的思路完成后续证明过程;(2)、如图3,以为直径的半圆上有一点P, , 直线l与相切于点P,过点于点E,交于点Q,求出的长.26. 在如图1所示的平面直角坐标系中,O为原点, ⊙C的圆心坐标为(−2,−2),半径为 , 直线y=−x+2与x轴,y轴分别交于点A,B,点P在线段AB上运动(包括端点).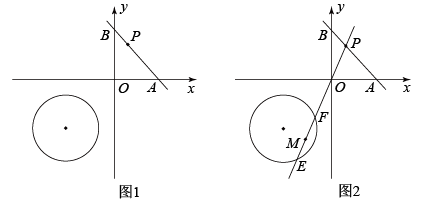 (1)、直线CO与AB的夹角是;(2)、当是等腰三角形时,求点P的坐标;(3)、当直线与相切时,求的度数;(4)、如图2.直线与相交于点E,F,M为线段的中点,当点P在线段上运动时,点M也相应运动,请直接写出点M所经过路径的长度.
(1)、直线CO与AB的夹角是;(2)、当是等腰三角形时,求点P的坐标;(3)、当直线与相切时,求的度数;(4)、如图2.直线与相交于点E,F,M为线段的中点,当点P在线段上运动时,点M也相应运动,请直接写出点M所经过路径的长度.