北京顺义区2022年中考二模数学试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列几何体中，其侧面展开图为扇形的是（）

A、 B、 C、 D、

查看试题解析
2. 我国成功发射北斗系统第55颗导航卫星，暨北斗三号最后一颗全球组网卫星，该卫星距离地面约36000千米．将36000用科学记数法表示应为（）

A、3.6×10³ B、3.6×10⁴ C、36×10³ D、0.36×10⁵

查看试题解析
3. 下列图形中既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 实数a，b，c在数轴上对应点的位置如图所示，若 $| a | = | c |$ ，则下列结论中正确的是（）

A、 $a + c > 0$ B、 $a - b > 0$ C、 $| a | > b$ D、 $a b > 0$

查看试题解析
5. 如图， $A B ∥ C D$ ， $∠ A = 30 °$ ， DA平分∠CDE，则∠DEB的度数为（）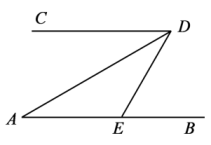

A、75° B、60° C、45° D、30°

查看试题解析
6. 方程 $\frac{2}{x} - \frac{1}{x - 2} = 0$ 的解是（）

A、4 B、3 C、2 D、1

查看试题解析
7. 已知三个点（x₁ ， y₁），（x₂ ， y₂），（x₃ ， y₃）在反比例函数y＝ $\frac{2}{x}$ 的图象上，其中x₁＜x₂＜0＜x₃ ，下列结论中正确的是（）

A、y₂＜y₁＜0＜y₃ B、y₁＜y₂＜0＜y₃ C、y₃＜0＜y₂＜y₁ D、y₃＜0＜y₁＜y₂

查看试题解析
8. 某超市的某种蔬菜一周内每天的进价与售价信息和实际每天的销售量情况如图表所示，则下列推断不合理的是（）
该种蔬菜一周内实际销售量表（单位：斤）
日期
周一
周二
周三
周四
周五
周六
周日
销售量
30
40
35
30
50
60
50

A、销售该种蔬菜周一的利润最小 B、销售该种蔬菜周日的利润最大 C、该种蔬菜一周中每天的售价组成的这组数据的众数是4 D、该种蔬菜一周中每天进价组成的这组数据的中位数是3

查看试题解析

二、填空题

9. 若分式 $\frac{x - 2}{x + 1}$ 的值为0，则x的值是．

查看试题解析
10. 一个正多边形的内角和为 $720 °$ ，则这个多边形的外角的度数为.

查看试题解析
11. 已知 $a < \sqrt{15} < b$ ，且a、b为两个连续的整数，则a+b＝．

查看试题解析
12. 如果关于x的方程 $x^{2} + 4 x + m = 0$ 有实数根，那么m的取值范围是．

查看试题解析
13. 如图，AD，BE是 $△ A B C$ 的两条高线，只需添加一个条件即可证明 $△ A D C ≌ △ B E C$ （不添加其它字母及辅助线），这个条件可以是（写出一个即可）．

查看试题解析

14. 柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下，对某植物种子发芽率进行研究时所得到的数据：

种子数n	30	75	130	210	480	856	1250	2300
发芽数m	28	72	125	200	457	814	1187	2185
发芽频率 $\frac{m}{n}$	0.9333	0.9600	0.9615	0.9524	0.9521	0.9509	0.9496	0.9500

依据上面的数据可以估计，这种植物种子在该实验条件下发芽的概率约是(结果精确到0.01).

查看试题解析

15. 幻方历史悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方．将数字1~9分别填入如图所示的幻方中，要求每一横行，每一竖行以及两条对角线上的数字之和都是15，则a的值为．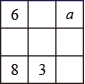

查看试题解析
16. 某中学为积极开展校园足球运动，计划购买A和B两种品牌的足球，已知一个A品牌足球价格为120元，一个B品牌足球价格为150元．学校准备用3000元购买这两种足球（两种足球都买），并且3000元全部用完，则该校共有种购买方案．

查看试题解析

三、解答题

17. 计算： $\sqrt{18} - 4 c o s 45 ° + | - 2 | - {(1 - \sqrt{2})}^{0}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 5 x + 2 \geq 4 x - 1 ， \\ \frac{x + 1}{4} > \frac{x - 3}{2} + 1 . \end{array}$

查看试题解析
19. 已知 $x^{2} + 3 x - 2 = 0$ ，求代数式 $(2 x + y) (2 x - y) - 2 x (x - 3) + y^{2}$ 的值．

查看试题解析
20. 已知：如图，直线l和l外一点P．
求作：直线PQ，使得 $P Q ∥ l$ ．
作法：①在直线l上任取一点A，连接PA，以点A为圆心，PA的长为半径画弧，交直线l于点B；
②分别以点P，B为圆心，PA的长为半径画弧，两弧交于点Q（不与点A重合）；
③作直线PQ．
所以直线PQ就是所求作的直线．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接BQ．
∵ $A B = B Q = P Q = P A$ ，
∴四边形PABQ是 ▲ ，（）（填推理依据）．
∴ $P Q ∥ A B$ （）（填推理依据）．
即 $P Q ∥ l$ ．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C$ ， AD为BC边上的中线，点E为AD的中点，过点A作 $A F ∥ B C$ ，交BE的延长线于点F，连接CF．

(1)、求证：四边形ADCF为矩形；

(2)、若 $B C = 12$ ， $s i n ∠ A C B = \frac{4}{5}$ ，求EF的长．

查看试题解析
22. 在平面直角坐标系xOy中，直线l： $y = k x - k + 4$ 与函数 $y = \frac{m}{x} (x > 0)$ 的图象交于点 $A (1 ， 4)$ ．

(1)、求m的值；

(2)、横、纵坐标都是整数的点叫做整点．记直线l与函数 $y = \frac{m}{x} (x > 0)$ 的图象所围成的区域（不含边界）为W．点 $B (n ， 1)$ （ $n \geq 4$ ， n为整数）在直线l上．
①当 $n = 5$ 时，求k的值，并写出区域W内的整点个数；
②当区域W内恰有5个整点时，直接写出n和k的值．

查看试题解析
23. 如图， $△ A B C$ 内接于 $⊙ O$ ， AB是 $⊙ O$ 的直径，点D在AB的延长线上，且 $∠ B C D = ∠ A$ ，点E为AC的中点，连接OE并延长与DC的延长线交于点F．

(1)、求证：CD是 $⊙ O$ 的切线；

(2)、若 $C D = 4$ ， $t a n A = \frac{1}{2}$ ，求CF的长．

查看试题解析
24. 如图是某抛物线形拱桥的截面图．某数学小组对这座拱桥很感兴趣，他们利用测量工具测出水面AB的宽为8米．设AB上的点E到点A的距离 $A E = x$ 米，点E到拱桥顶面的垂直距离 $E F = y$ 米．
通过取点、测量，数学小组的同学得到了x与y的几组值，如下表：
x（米）
0
1
2
3
4
5
6
7
8
y（米）
0
1.75
3
3.75
4
3.75
3
1.75
0

(1)、拱桥顶面离水面AB的最大高度为米；

(2)、请你帮助该数学小组建立平面直角坐标系，描出上表中各对对应值为坐标的点，并用平滑的曲线连接；

(3)、测量后的某一天，由于降雨原因，水面比测量时上升1米．现有一游船（截面为矩形）宽度为4米，船顶到水面的高度为2米．要求游船从拱桥下面通过时，船顶到拱桥顶面的距离应大于0.5米．结合所画图象，请判断该游船是否能安全通过：（填写“能”或“不能”）．

查看试题解析
25. 为整体提升学生的综合素质，某中学利用课后服务时间，对八年级300名学生全员开设了A，B，C三类课程，经过一个学期的课程学习，学校想了解学生课程学习效果，从中随机抽取20名学生进行了检测，获得了他们的成绩（百分制），并对数据（成绩）进行整理、描述和分析．这20名学生A，B，C三类课程的成绩情况统计图如下：

(1)、①学生甲A类课程的成绩是98分，则该生C类课程的成绩是分；
②学生乙C类课程的成绩是45分，则该生三类课程的平均成绩是分；

(2)、补全这20名学生B类课程成绩的频数分布直方图；
（数据分成7组： $30 \leq x < 40$ ， $40 \leq x < 50$ ， $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ）．

(3)、若成绩在85分及以上为优秀，估计该校八年级学生A类课程成绩优秀的人数．

查看试题解析
26. 在平面直角坐标系xOy中，已知抛物线 $y = x^{2} + m x + n$ ．

(1)、当 $m = - 3$ 时，
①求抛物线的对称轴；
②若点 $A (1 ， y_{1})$ ， $B (x_{2} ， y_{2})$ 都在抛物线上，且 $y_{2} < y_{1}$ ，求 $x_{2}$ 的取值范围；

(2)、已知点 $P (- 1 ， 1)$ ，将点P向右平移3个单位长度，得到点Q．当 $n = 2$ 时，若抛物线与线段PQ恰有一个公共点，结合函数图象，求m的取值范围．

查看试题解析
27. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， P，D为射线AB上两点（点D在点P的左侧），且 $P D = B C$ ，连接CP．以P为中心，将线段PD逆时针旋转 $n ° (0 < n < 180)$ 得线段PE．

(1)、如图1，当四边形ACPE是平行四边形时，画出图形，并直接写出n的值；

(2)、当 $n = 135 °$ 时，M为线段AE的中点，连接PM．
①在图2中依题意补全图形；
②用等式表示线段CP与PM之间的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系xOy中，对于点R和线段PQ，给出如下定义：M为线段PQ上任意一点，如果R，M两点间的距离的最小值恰好等于线段PQ的长，则称点R为线段PQ的“等距点”．

(1)、已知点 $A (5 ， 0)$ ．
①在点 $B_{1} (- 3 ， 4)$ ， $B_{2} (1 ， 5)$ ， $B_{3} (4 ， - 3)$ ， $B_{4} (3 ， 6)$ 中，线段OA的“等距点”是 ▲ ；
②若点C在直线 $y = 2 x + 5$ 上，并且点C是线段OA的“等距点”，求点C的坐标；

(2)、已知点 $D (1 ， 0)$ ，点 $E (0 ， - 1)$ ，图形W是以点 $T (t ， 0)$ 为圆心，1为半径的 $⊙ T$ 位于x轴及x轴上方的部分．若图形W上存在线段DE的“等距点”，直接写出t的取值范围．

查看试题解析

日期	周一	周二	周三	周四	周五	周六	周日
销售量	30	40	35	30	50	60	50

x（米）	0	1	2	3	4	5	6	7	8
y（米）	0	1.75	3	3.75	4	3.75	3	1.75	0