北京市门头沟区2022年九年级中考二模数学试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 在下面四个几何体中，俯视图是矩形的是（）

A、 B、 C、 D、

查看试题解析
2. 2022年5月4日我国“巅峰使命2022”珠峰科考13名科考登山队员全部登顶珠穆朗玛主峰成功，并在海拔超过8 800米处架设了自动气象观测站，这是全世界海拔最高的自动气象观测站．将数字8 800用科学记数法表示为（）

A、8.8×10³ B、88×10² C、8.8×10⁴ D、0.88×10⁵

查看试题解析
3. 2022年2月4日至20日第二十四届冬季奥林匹克运动会在北京成功举办，下面是一些北京著名建筑物的简笔画，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，如果数轴上A、B两点分别对应实数a、b，那么下列结论正确的是（）

A、a＋b＞0 B、ab＞0 C、a－b＞0 D、|a|－|b|＞0

查看试题解析
5. 如果 $a - b = 2 \sqrt{3}$ ，那么代数式 $(\frac{a^{2} + b^{2}}{2 a} - b) \cdot \frac{a}{a - b}$ 的值为（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
6. 十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒.当你抬头看信号灯时，是黄灯的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{5}{12}$ C、 $\frac{1}{3}$ D、 $\frac{1}{12}$

查看试题解析
7. 如图，在⊙O中， AB是直径，CD丄AB，∠ACD = 60°，OD = 2，那么DC的长等于（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、2 D、4

查看试题解析
8. 在平面直角坐标系xOy中，已知抛物线 $y = a x^{2} - 2 a x + 4$ （ $a > 0$ ），如果点A（ $m - 1$ ， $y_{1}$ ），B（m， $y_{2}$ ）和C（ $m + 2$ ， $y_{3}$ ）均在该抛物线上，且总有 $y_{1} > y_{3} > y_{2}$ ，结合图象，可知m的取值范围是（）

A、 $m < 1$ B、 $0 < m < 1$ C、 $m < \frac{1}{2}$ D、 $0 < m < \frac{1}{2}$

查看试题解析

二、填空题

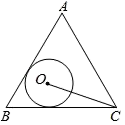
9. 式子 $\sqrt{3 + x}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
10. 分解因式： $a b^{2} - a c^{2}$ =.

查看试题解析
11. 若 $| x + 2 | + \sqrt{y - 3} =$ 0，则 $x y =$ ．

查看试题解析
12. 《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”译文大致是：“用一根绳子去量一根木条，绳子剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺？”如果设木条长x尺，绳子长y尺，可列方程组为；

查看试题解析
13. 如图，半径为 $\sqrt{3}$ 的⊙ $O$ 与边长为 $8$ 的等边三角形 $A B C$ 的两边 $A B$ 、 $B C$ 都相切，连接 $O C$ ，则 $\tan ∠ O C B =$ .

查看试题解析
14. 已知y是以x为自变量的二次函数，且当x=0时，y的最小值为-1，写出一个满足上述条件的二次函数表达式．

查看试题解析
15. 在平行四边形ABCD中，对角线AC，BD交于点O，只需添加一个条件，即可证明平行四边形ABCD是矩形，这个条件可以是（写出一个即可）．

查看试题解析
16. 电脑系统中有个“扫雷”游戏，游戏规定：一个方块里最多有一个地雷，方块上面如果标有数字，则是表示此数字周围的方块中地雷的个数．如图1中的“3”就是表示它周围的八个方块中有且只有3个有地雷．如图2，这是小明玩游戏的局部，图中有4个方块已确定是地雷（标旗子处），其它区域表示还未掀开，问在标有“A”~“G”的七个方块中，能确定一定是地雷的有（填方块上的字母）．

查看试题解析

三、解答题

17. 计算： ${(\frac{1}{3})}^{- 1} + \sqrt{18} + | - 2 | - 6 \sin 45 °$

查看试题解析
18. 解不等式 $\frac{1}{2} x - 1 \leq \frac{2}{3} x - \frac{1}{2}$ ，并把它的解集在数轴上表示出来．

查看试题解析
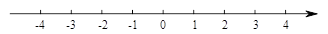19. 下面是小明同学设计的“作圆的内接正方形”的尺规作图过程．
已知：如图，⊙O．
求作：⊙O的内接正方形．
作法：① 作⊙O的直径AB；
② 分别以点A，B为圆心，大于 $\frac{1}{2}$ AB同样长为半径作弧，两弧交于M，N；
③ 作直线MN交⊙O于点C，D；
④ 连接AC，BC，AD，BD．
∴ 四边形ACBD就是所求作的正方形．
根据小明设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：∵ MN是AB的      ▲ ，
∴ ∠AOC = ∠COB = ∠BOD = ∠DOA = 90°．
∴  AC = BC = BD = AD．（                      ）（填推理依据）
∴ 四边形ACBD是菱形．
又∵AB是⊙O的直径，
∴ ∠ACB = 90°．（                      ）（填推理依据）
∴ 四边形ACBD是正方形．

查看试题解析
20. 已知关于x的二次方程 $m x^{2} - (2 m - 3) x + (m - 1) = 0$ 有两个不相等的实数根．

(1)、求m的取值范围；

(2)、如果m为正整数，求此方程的根．

查看试题解析
21. 如图，在矩形ABCD得对角线AC，BD交于点O，延长CD到点E，使 $D E = C D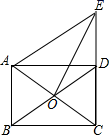$ ，连接AE．

(1)、求证：四边形ABDE是平行四边形；

(2)、连接OE，若 $A D = 4$ ， $A B = 2$ ，求OE的长．

查看试题解析
22. 如图，一次函数 $y_{1} = - x + 2$ 的图象与反比例函数 $y_{2} = \frac{k}{x}$ 的图象相交于A、B两点，点B的坐标为（2n，－n）．

(1)、求n的值，并确定反比例函数的表达式；

(2)、结合函数图象，直接写出不等式 $\frac{k}{x} > - x + 2$ 的解集．

查看试题解析
23. 如图，杂技团进行杂技表演，演员要从跷跷板右端A处弹跳后恰好落在人梯的顶端B处，其身体（看成一点）的路径是一条抛物线．现测量出如下的数据，设演员身体距起跳点A水平距离为d米时，距地面的高度为h米．
d（米）
…
1.00
1.50
2.00
2.50
3.00
3.50
…
h（米）
…
3.40
4.15
4.60
4.75
4.60
4.15
…
请你解决以下问题：

(1)、在下边网格中建立适当平面直角坐标系，根据已知数据描点，并用平滑曲线连接；

(2)、结合表中所给的数据或所画的图象，直接写出演员身体距离地面的最大高度；

(3)、求起跳点A距离地面的高度；

(4)、在一次表演中，已知人梯到起跳点A的水平距离是3米，人梯的高度是3.40米．问此次表演是否成功？如果成功，说明理由；如果不成功，说明应怎样调节人梯到起跳点A的水平距离才能成功？

查看试题解析
24. 如图，已知Rt△ABC中，∠ACB＝90°，E为AB上一点，以AE为直径作⊙O与BC相切于点D，连接ED并延长交AC的延长线于点F．

(1)、求证：AE＝AF；

(2)、若AE＝5，AC＝4，求BE的长．

查看试题解析
25. 2021年7月24日中共中央办公厅、国务院办公厅颁布了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》，该意见对学生睡眠时间提出了新的要求．为了了解某校初二年级学生的睡眠时长，随机抽取了初二年级男生和女生各20位，对其同一天的睡眠时长进行调查，并对数据进行收集、整理、描述和分析．下面给出了相关信息．
a．睡眠时长（单位：小时）：
男生
7.7
9.9
9.8
5.5
9.6
9.6
8.6
9.8
9.9
7.9
9.0
7.5
7.7
8.5
9.2
8.7
9.2
9.3
9.2
9.4
女生
9.0
7.6
9.1
9.0
8.0
7.9
8.6
9.2
9.0
9.3
8.2
9.2
8.8
8.5
9.1
8.6
9.0
9.5
9.3
9.1
b．睡眠时长频数直方图（分组：5≤x＜6，6≤x＜7，7≤x＜8，8≤x＜9，9≤x＜10）：
c．睡眠时长的平均数、众数、中位数如下：
年级
平均数
众数
中位数
男生
8.8
m
9.2
女生
8.8
9.0
n
根据以上信息，回答下列问题：

(1)、补全男生睡眠时长频数分布直方图；

(2)、直接写出表中m，n的值；

(3)、根据抽样调查情况，可以推断（填“男生”或“女生”）睡眠情况比较好，理由为．

查看试题解析
26. 在平面直角坐标系中xOy中，已知抛物线 $y = m x^{2} - 2 m x + m - 4$ （ $m \neq 0$ ）．

(1)、求此抛物线的对称轴；

(2)、当 $m = 1$ 时，求抛物线的表达式；

(3)、如果将（2）中的抛物线在x轴下方的部分沿x轴向上翻折，得到的图象与剩余的图象组成新图形M．
①直接写直线 $y = x + 1$ 与图形M公共点的个数；
②当直线 $y = k (x + 2) - 1$ （ $k \neq 0$ ）与图形M有两个公共点时，直接写出k的取值范围．

查看试题解析
27. 如图，在△ABC中，∠ACB = 90°，D是BC的中点，过点C作CE⊥AD，交AD于点E，交AB于点F，作点E关于直线AC的对称点G，连接AG和GC，过点B作BM⊥GC交GC的延长线于点M ．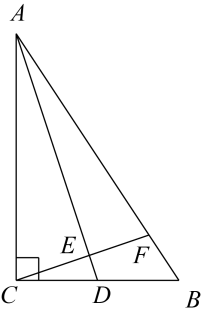

(1)、① 根据题意，补全图形；
② 比较∠BCF与∠BCM的大小，并证明．

(2)、过点B作BN⊥CF交CF的延长线于点N，用等式表示线段AG，EN与BM的数量关系，并证明．

查看试题解析
28. 我们规定：如图，点 $H$ 在直线 $M N$ 上，点 $P$ 和点 $P^{'}$ 均在直线 $M N$ 的上方，如果 $H P = H P^{'}$ ， $∠ P H M = ∠ P^{'} H N$ ，点 $P^{'}$ 就是点 $P$ 关于直线 $M N$ 的“反射点”，其中点 $H$ 为“ $V$ 点”，射线 $H P$ 与射线 $H P^{'}$ 组成的图形为“ $V$ 形”．
在平面直角坐标系 $x O y$ 中，

(1)、如果点 $P (0 ， 3)$ ， $H (1.5 ， 0)$ ，那么点 $P$ 关于 $x$ 轴的反射点 $P^{'}$ 的坐标为；

(2)、已知点 $A (0 ， a)$ ，过点 $A$ 作平行于 $x$ 轴的直线 $l$ ．
①如果点 $B (5 ， 3)$ 关于直线 $l$ 的反射点 $B^{'}$ 和“ $V$ 点”都在直线 $y = - x + 4$ 上，求点 $B^{'}$ 的坐标和 $a$ 的值；
② $⊙ W$ 是以 $(3 ， 2)$ 为圆心， $1$ 为半径的圆，如果某点关于直线 $l$ 的反射点和“ $V$ 点”都在直线 $y = - x + 4$ 上，且形成的“ $V$ 形”恰好与 $⊙ W$ 有且只有两个交点，求 $a$ 的取值范围．

查看试题解析

d（米）	…	1.00	1.50	2.00	2.50	3.00	3.50	…
h（米）	…	3.40	4.15	4.60	4.75	4.60	4.15	…

男生	7.7	9.9	9.8	5.5	9.6	9.6	8.6	9.8	9.9	7.9
男生	9.0	7.5	7.7	8.5	9.2	8.7	9.2	9.3	9.2	9.4
女生	9.0	7.6	9.1	9.0	8.0	7.9	8.6	9.2	9.0	9.3
女生	8.2	9.2	8.8	8.5	9.1	8.6	9.0	9.5	9.3	9.1