北京市丰台区2022年九年级数学二模试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 如图,下列水平放置的几何体中,侧面展开图是扇形的是( )A、
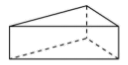 B、
B、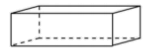 C、
C、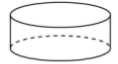 D、
D、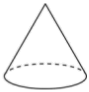 2. 2021年我国原油产量约1.99亿吨,连续3年回升.将199 000 000用科学记数法表示应为( )A、 B、 C、 D、3. 如图.AB∥CD,∠ACD=80°,∠ACB=30°,∠B的度数为( )
2. 2021年我国原油产量约1.99亿吨,连续3年回升.将199 000 000用科学记数法表示应为( )A、 B、 C、 D、3. 如图.AB∥CD,∠ACD=80°,∠ACB=30°,∠B的度数为( )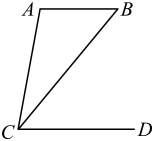 A、50° B、45° C、30° D、25°4. 下列多边形中,内角和最大的是( )A、
A、50° B、45° C、30° D、25°4. 下列多边形中,内角和最大的是( )A、 B、
B、 C、
C、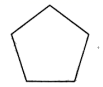 D、
D、 5. 实数a,b在数轴上的对应点的位置如图所示,若实数c满足 , 则c的值可以是( )
5. 实数a,b在数轴上的对应点的位置如图所示,若实数c满足 , 则c的值可以是( )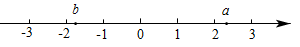 A、-3 B、-2 C、2 D、36. 一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上的概率是( )A、 B、 C、 D、7. 若n为整数,且 , 则n的值是( )A、7 B、8 C、9 D、108. 如图,某容器的底面水平放置,匀速地向此容器内注水,在注满水的过程中,水面的高度h与时间t的函数关系的图象大致是( )
A、-3 B、-2 C、2 D、36. 一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上的概率是( )A、 B、 C、 D、7. 若n为整数,且 , 则n的值是( )A、7 B、8 C、9 D、108. 如图,某容器的底面水平放置,匀速地向此容器内注水,在注满水的过程中,水面的高度h与时间t的函数关系的图象大致是( ) A、
A、 B、
B、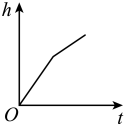 C、
C、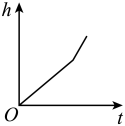 D、
D、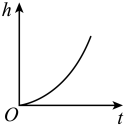
二、填空题
-
9. 式子 在实数范围内有意义,则 x 的取值范围是 .10. 方程的解是 .11. 已知关于x的方程x2﹣2x+m=0有两个不相等的实数根,则m的取值范围是 .
12. 如图,PA,PB是⊙O的切线,A,B为切点,点C在⊙O上,若 , 则∠ACB=°.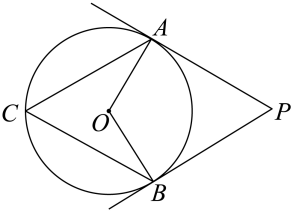 13. 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,连接EF,只需添加一个条件即可证明四边形EFCB是菱形,这个条件可以是(写出一个即可).
13. 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,连接EF,只需添加一个条件即可证明四边形EFCB是菱形,这个条件可以是(写出一个即可).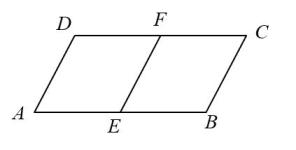 14. 在直角坐标系 中,直线 与双曲线 交于A,B两点.若点A,B的横坐标分别为 , ,则 的值为 .15. 甲、乙两台包装机同时包装糖果,分别从中随机抽取5袋,测得它们的实际质量(单位:g)如下表所示:
14. 在直角坐标系 中,直线 与双曲线 交于A,B两点.若点A,B的横坐标分别为 , ,则 的值为 .15. 甲、乙两台包装机同时包装糖果,分别从中随机抽取5袋,测得它们的实际质量(单位:g)如下表所示:甲
100
102
99
101
98
乙
100
97
104
97
102
那么包装机包装的5袋糖果的质量比较稳定(填“甲”或“乙”).
16. 某超市现有n个人在收银台排队等候结账.设结账人数按固定的速度增加,收银员结账的速度也是固定的.若同时开放2个收银台,需要20分钟可使排队等候人数为0;若同时开放3个收银台,需要12分钟可使排队等候人数为0.为减少顾客等待结账的时间,需要6分钟内使排队等候人数为0,则需要至少同时开放个收银台.三、解答题
-
17. 计算:18. 解不等式组: .19. 已知 , 求代数式的值.20. 已知:如图,射线AM.

求作:△ABC,使得 , .
作法:①在射线AM上任取一点O(不与点A重合);
②以点O为圆心,OA长为半径画弧,交射线AM于A,C两点;
③以点C为圆心,CO长为半径画弧,交于点B;
④连接AB,BC.
△ABC就是所求作的三角形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明:证明:连接OB.
在⊙O中,OB=OC
在⊙C中,OC==BC
∴OB=OC=BC
∴△OCB是等边三角形
∴
∵AC是⊙O的直径,
∴∠ABC= ▲ °( )(填推理的依据).
∴
∴ .
21. 如图,在△ABC中, , AD⊥BC,垂足为D,AE∥BC,CE∥DA.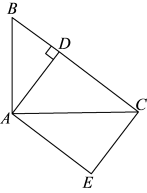 (1)、求证:四边形AECD是矩形;(2)、若AB=5, , 求AE的长.22. 在平面直角坐标系xOy中,一次函数的图象由函数的图象向下平移4个单位长度得到.(1)、求这个一次函数的解析式;(2)、一次函数的图象与x轴的交点为A,函数的图象与一次函数的图象的交点为B,记线段OA,AB,BO围成的区域(不含边界)为W,横、纵坐标都是整数的点叫做整点,若区域W内恰有2个整点,直接写出m的取值范围.23. 如图,AB是⊙O的直径,C为BA延长线上一点,过点C作⊙O的切线,切点为D,过点B作BE⊥CD于点E,连接AD,BD.
(1)、求证:四边形AECD是矩形;(2)、若AB=5, , 求AE的长.22. 在平面直角坐标系xOy中,一次函数的图象由函数的图象向下平移4个单位长度得到.(1)、求这个一次函数的解析式;(2)、一次函数的图象与x轴的交点为A,函数的图象与一次函数的图象的交点为B,记线段OA,AB,BO围成的区域(不含边界)为W,横、纵坐标都是整数的点叫做整点,若区域W内恰有2个整点,直接写出m的取值范围.23. 如图,AB是⊙O的直径,C为BA延长线上一点,过点C作⊙O的切线,切点为D,过点B作BE⊥CD于点E,连接AD,BD.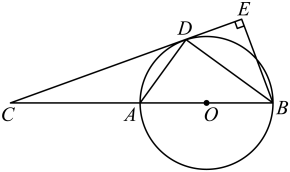 (1)、求证:;(2)、如果CA=AB,BD=4,求BE的长.24. 跳台滑雪是冬季奥运会比赛项目之一.记运动员在该项目的运动过程中的某个位置与起跳点的水平距离为x(单位:m),竖直高度为y(单位:m),下面记录了甲运动员起跳后的运动过程中的七组数据:
(1)、求证:;(2)、如果CA=AB,BD=4,求BE的长.24. 跳台滑雪是冬季奥运会比赛项目之一.记运动员在该项目的运动过程中的某个位置与起跳点的水平距离为x(单位:m),竖直高度为y(单位:m),下面记录了甲运动员起跳后的运动过程中的七组数据:x/m
0
10
20
30
40
50
60
y/m
54.0
57.8
57.6
53.4
45.2
33.0
16.8
下面是小明的探究过程,请补充完整:
(1)、为观察y与x之间的关系,建立坐标系,以x为横坐标,y为纵坐标,描出表中数据对应的7个点,并用平滑的曲线连接它们: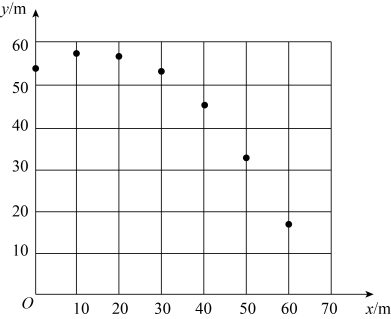 (2)、观察发现,(1)中的曲线可以看作是的一部分(填“抛物线”或“双曲线”),结合图象,可推断出水平距离约为m(结果保留小数点后一位)时,甲运动员起跳后达到最高点;(3)、乙运动员在此跳台进行训练,若乙运动员在运动过程中的最高点的竖直高度达到61m,则乙运动员运动中的最高点比甲运动员运动中的最高点(填写“高”或“低”)约m(结果保留小数点后一位).25. 2022年是中国共产主义青年团建团100周年,某校团委组织七、八年级学生开展主题为“成团百年,勇当先锋”的团史知识学习活动,为了解这两个年级学生团史知识的学习情况,从七、八年级的学生中,各随机抽取了20名学生进行测试,获得了他们的成绩(百分制,且成绩均为整数),并对数据(成绩)进行了整理、描述和分析,下面给出了部分信息.
(2)、观察发现,(1)中的曲线可以看作是的一部分(填“抛物线”或“双曲线”),结合图象,可推断出水平距离约为m(结果保留小数点后一位)时,甲运动员起跳后达到最高点;(3)、乙运动员在此跳台进行训练,若乙运动员在运动过程中的最高点的竖直高度达到61m,则乙运动员运动中的最高点比甲运动员运动中的最高点(填写“高”或“低”)约m(结果保留小数点后一位).25. 2022年是中国共产主义青年团建团100周年,某校团委组织七、八年级学生开展主题为“成团百年,勇当先锋”的团史知识学习活动,为了解这两个年级学生团史知识的学习情况,从七、八年级的学生中,各随机抽取了20名学生进行测试,获得了他们的成绩(百分制,且成绩均为整数),并对数据(成绩)进行了整理、描述和分析,下面给出了部分信息.a.该校七年级抽取的学生测试成绩的数据的频数分布直方图如下(数据分为5组 , , , , )
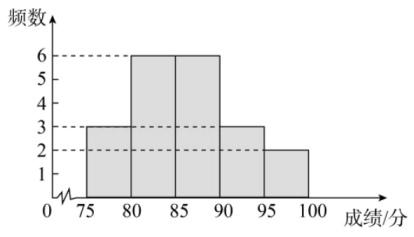
b.该校七年级抽取的学生测试成绩的数据在这一组的是:85;85;85;86;87;88
c.该校七、八年级抽取的学生的测试成绩的数据的平均数、中位数、众数如下:
平均数
中位数
众数
七年级
85.2
m
85
八年级
87
89.5
90
根据以上信息,回答下列问题:
(1)、写出表中m的值;(2)、此次测试成绩90分及90分以上为优秀.①记该校七年级抽取的学生中成绩优秀的人数是 , 八年级抽取的学生中成绩优秀的人数为 , 比较 , 的大小,并说明理由;
②该校七、八年级各有200名学生,假设该校七、八年级学生全部参加此次测试,请估计成绩优秀的学生总人数(直接写出结果).
26. 在平面直角坐标系xOy中,已知抛物线 .(1)、求该抛物线的对称轴(用含a的式子表示)(2)、 , 为该抛物线上的两点,若 , , 且 , 求a的取值范围.27. 如图,在△ABC中,AB=AC,∠BAC=120°,D是BC中点,连接AD.点M在线段AD上(不与点A,D重合),连接MB,点E在CA的延长线上且ME=MB,连接EB.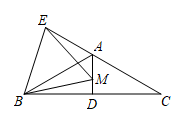 (1)、比较∠ABM与∠AEM的大小,并证明;(2)、用等式表示线段AM,AB,AE之间的数量关系,并证明.28. 在平面直角坐标系xOy中,⊙O的半径为1,A为任意一点,B为⊙O上任意一点,给出如下定义:记A,B两点间的距离的最小值为p(规定:点A在⊙O上时,),最大值为q,那么把的值称为点A与⊙O的“关联距离”,记作d(A,⊙O)(1)、如图,点D,E,F的横、纵坐标都是整数
(1)、比较∠ABM与∠AEM的大小,并证明;(2)、用等式表示线段AM,AB,AE之间的数量关系,并证明.28. 在平面直角坐标系xOy中,⊙O的半径为1,A为任意一点,B为⊙O上任意一点,给出如下定义:记A,B两点间的距离的最小值为p(规定:点A在⊙O上时,),最大值为q,那么把的值称为点A与⊙O的“关联距离”,记作d(A,⊙O)(1)、如图,点D,E,F的横、纵坐标都是整数①d(D,⊙O)= ▲ ;
②若点M在线段EF上,求d(M,⊙O)的取值范围;
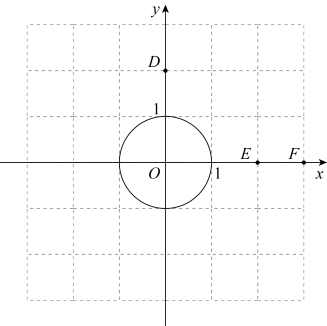 (2)、若点N在直线上,直接写出d(N,⊙O)的取值范围;(3)、正方形的边长为m,若点P在该正方形的边上运动时,满足d(P,⊙O)的最小值为1,最大值为 , 直接写出m的最小值和最大值.
(2)、若点N在直线上,直接写出d(N,⊙O)的取值范围;(3)、正方形的边长为m,若点P在该正方形的边上运动时,满足d(P,⊙O)的最小值为1,最大值为 , 直接写出m的最小值和最大值.