北京市东城区2022年九年级二模数学试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 国家速滑馆是2022年北京冬奥会北京主赛区标志性场馆，是唯一新建的冰上竞赛场馆．国家速滑馆拥有亚洲最大的全冰面设计，冰面面积达12000平方米．将12000用科学记数法表示应为（）

A、 $12 \times 1 0^{3}$ B、 $1.2 \times 1 0^{4}$ C、 $1.2 \times 1 0^{5}$ D、 $0.12 \times 1 0^{5}$

查看试题解析
2. 如图是某一几何体的展开图，该几何体是（）

A、三棱柱 B、四棱柱 C、圆柱 D、圆锥

查看试题解析
3. 如图，点 $O$ 在直线 $A B$ 上， $O C ⊥ O D$ ．若 $∠ B O D = 30 °$ ，则 $∠ A O C$ 的大小为（）

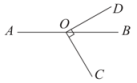A、120° B、130° C、140° D、150°

查看试题解析
4. 下列图形中，既是中心对称图形又是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 方程组的解是 ${\begin{array}{l} x + y = 3 \\ x - y = - 1 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = - 3 \\ y = - 2 \end{array}$ C、 ${\begin{array}{l} x = 2 ， \\ y = 1 . \end{array}$ D、 ${\begin{array}{l} x = 2 ， \\ y = 3 . \end{array}$

查看试题解析
6. 下列运算结果正确的是（）

A、 $3 a - a = 2$ B、 $a^{2} \cdot a^{4} = a^{8}$ C、 $(a + 2) (a - 2) = a^{2} - 4$ D、 ${(- a)}^{2} = - a^{2}$

查看试题解析
7. 在平面直角坐标系中，将点M（4，5）向左平移3个单位，再向上平移2个单位，则平移后的点的坐标是（）

A、（1，3） B、（7，7） C、（1，7） D、（7，3）

查看试题解析
8. 从1980年初次征战冬奥会，到1992年取得首枚冬奥会奖牌，再到2022年北京冬奥会金牌榜前三，中国的冰雪体育事业不断取得突破性成绩．历届冬奥会的比赛项目常被分成两大类：冰项目和雪项目．根据统计图提供的信息，有如下四个结论：
①中国队在2022年北京冬奥会上获得的金牌数是参加冬奥会以来最多的一次；②中国队在2022年北京冬奥会上获得的奖牌数是参加冬奥会以来最多的一次；③中国队在冬奥会上的冰上项目奖牌数逐年提高；④中国队在冬奥会上的雪上项目奖牌数在2022年首次超越冰上项目奖牌数．
上述结论中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 若分式 $\frac{x}{x + 1}$ 的值为0，则x的值是.

查看试题解析
10. 分解因式： $2 x^{2} - 12 x + 18 =$ .

查看试题解析
11. 写一个当x＞0时，y随x的增大而增大的函数解析式．

查看试题解析
12. 计算： $\frac{a}{a - 2} + \frac{2}{2 - a} =$ ．

查看试题解析
13. 据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验，阐释了光的直线传播原理，如图（1）所示。如图（2）所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是6cm，则蜡烛火焰的高度是cm．

查看试题解析
14. 不透明布袋中有红、黄小球各一个，除颜色外无其他差别．随机摸出一个小球后，放回并摇匀．再随机摸出一个，则两次摸到的球中，一个红球、一个黄球的概率为．

查看试题解析
15. 如图，在边长为1的正方形网格中，点 $A ， B ， D$ 在格点上，以 $A B$ 为直径的圆过 $C ， D$ 两点，则 $s i n ∠ B C D$ 的值为．

查看试题解析
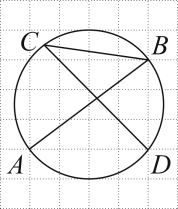16. 在一次数学活动课上，某数学老师将1～10共十个整数依次写在十张不透明的卡片上（每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下）．他先像洗扑克牌一样打乱这些卡片的顺序，然后把甲、乙、丙、丁、戊五位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上，写出的结果依次是：甲：11；乙：4；丙：15；丁：8；戊：17，则丙同学手里拿的卡片的数字是．

查看试题解析

三、解答题

17. 计算： ${(- 1)}^{2022} + \sqrt[3]{8} - {(\frac{1}{3})}^{- 1} + \sqrt{2} s i n 45 °$ ．

查看试题解析
18. 解不等式 $6 - 4 x \geq 3 x - 8$ ，并写出其正整数解．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = A C$ ．
求作：直线 $A D$ ，使得 $A D$ // $B C$ ．
小明的作法如下：
①以点A为圆心、适当长为半径画弧，交 $B A$ 的延长线于点 $E$ ，交线段 $A C$ 于点 $F$ ；
②分别以点 $E ， F$ 为圆心、大于 $\frac{1}{2} E F$ 的长为半径画弧，两弧在 $∠ E A C$ 的内部相交于点 $D$ ；
③画直线 $A D$ ．
直线 $A D$ 即为所求，

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明。
证明：由作法可知： $A D$ 平分 $∠ E A C$ ．
∴ $∠ E A D = ∠ D A C$ （      ）．（填推理的依据）
∵ $A B = A C$ ，
∴ $∠ B = ∠ C$
∵ $∠ E A C = ∠ B + ∠ C$ ，
∴ $∠ E A C = 2 ∠ B$ ．
∵ $∠ E A C = 2 ∠ E A D$ ，
∴ $∠ E A D =$       ▲ ．
∴ $A D$ // $B C$ （      ）．（填推理的依据）

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 k x + k^{2} - 1 = 0$ ．

(1)、不解方程，判断此方程根的情况；

(2)、若 $x = 2$ 是该方程的一个根，求代数式 $- 2 k^{2} + 8 k + 5$ 的值．

查看试题解析
21. 如图，在平行四边形 $A B C D$ 中， $D B = D A$ ，点 $F$ 是 $A B$ 的中点，连接 $D F$ 并延长，交 $C B$ 的延长线于点 $E$ ，连接 $A E$ ．

(1)、求证：四边形 $A E B D$ 是菱形；

(2)、若 $D C = \sqrt{10}$ ， $t a n ∠ D C B = 3$ ，求菱形 $A E B D$ 的边长．

查看试题解析
22. 如图，在平面直角坐标系 $x O y$ 中，双曲线 $y = \frac{k}{x} (k \neq 0)$ 经过点 $A (2 ， - 1)$ ，直线 $l$ ： $y = - 2 x + b$ 经过点 $B (2 ， - 2)$ ．

(1)、求k，b的值；

(2)、过点 $P (n ， 0) (n > 0)$ 作垂直于 $x$ 轴的直线，与双曲线 $y = \frac{k}{x} (k \neq 0)$ 交于点 $C$ ，与直线 $l$ 交于点 $D$ ．
①当 $n = 2$ 时，判断 $C D$ 与 $C P$ 的数量关系；
②当 $C D \leq C P$ 时，结合图象，直接写出 $n$ 的取值范围．

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B > A C$ ， $∠ B A C = 90 °$ ，在 $C B$ 上截取 $C D = C A$ ，过点 $D$ 作 $D E ⊥ A B$ 于点 $E$ ，连接AD，以点 $A$ 为圆心、 $A E$ 的长为半径作 $⊙ A$ ．

(1)、求证： $B C$ 是⊙A的切线；

(2)、若 $A C = 5$ ， $B D = 3$ ，求 $D E$ 的长．

查看试题解析

24. 某研究中心建立了自己的科技创新评估体系，并对2021年中国城市的科技创新水平进行了评估。科技创新综合指数由科技创新总量指数和科技创新效率指数组成（以下简称：综合指数、总量指数和效率指数）。该研究中心对2021年中国城市综合指数得分排名前40的城市的有关数据进行收集、整理、描述和分析。下面给出了部分信息：

a．综合指数得分的频数分布表（数据分成6组： $65.0 x \leq 70.0$ ， $70.0 \leq x < 75.0$ ， $75.0 \leq x < 80.0$ ， $80.0 \leq x < 85.0$ $85.0 \leq x < 90.0$ ， $90.0 \leq x < 95.0$ ）：

综合指数得分	频数
$65.0 x \leq 70.0$	8
$70.0 \leq x < 75.0$	16
$75.0 \leq x < 80.0$	8
$80.0 \leq x < 85.0$	$m$
$85.0 \leq x < 90.0$	2
$90.0 \leq x < 95.0$	1
合计	40

b．综合指数得分在 $70.0 \leq x < 75.0$ 这一组的是：

70.0 70.4 70.6 70.7 71.0 71.0 71.1 71.2 71.8 71.9 72.5 73.8 74.0 74.4 74.5 74.6

c.40个城市的总量指数与效率指数得分情况统计图：

（数据来源于网络《2021年中国城市科技创新指数报告》）

根据以上信息，回答下列问题：

(1)、综合指数得分的频数分布表中，m=；

(2)、40个城市综合指数得分的中位数为；

(3)、以下说法正确的是．

①某城市创新效率指数得分排名第1，该城市的总量指数得分大约是86.2分；

②大多数城市效率指数高于总量指数，可以通过提升这些城市的总量指数来提升城市的综合指数．

查看试题解析

25. 小强用竹篱笆围一个面积为 $\frac{9}{4}$ 平方米的矩形小花园，他考虑至少需要几米长的竹篱笆（不考虑接缝），根据学习函数的经验，他做了如下的探究，请你完善他的思考过程．

(1)、建立函数模型：
设矩形小花园的一边长为 $x$ 米，则矩形小花园的另一边长为米（用含 $x$ 的代数式表示）；若总篱笆长为 $y$ 米，请写出总篱笆长 $y$ （米）关于边长 $x$ （米）的函数关系式；

(2)、列表：
根据函数的表达式，得到了 $x$ 与 $y$ 的几组对应值，如下表：
$x$
$\frac{1}{2}$
1
$\frac{3}{2}$
2
$\frac{5}{2}$
3
$\frac{7}{2}$
4
$\frac{9}{2}$
5
$y$
10
$\frac{13}{2}$
6
$a$
$\frac{34}{5}$
$\frac{15}{2}$
$\frac{58}{7}$
$\frac{73}{8}$
$b$
$\frac{109}{10}$
表中a= ， b= ；

(3)、描点、画出函数图象：
如图，在平面直角坐标系 $x O y$ 中，将表中未描出的点 $(2 ， a)$ ， $(\frac{9}{2} ， b)$ 补充完整，并根据描出的点画出该函数的图象；

(4)、解决问题：
根据以上信息可得，当x=时，y有最小值．由此，小强确定篱笆长至少为米．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x + 1 (a \neq 0)$ 的对称轴是直线 $x = 3$ ．

(1)、直接写出抛物线与 $y$ 轴的交点坐标；

(2)、求抛物线的顶点坐标（用含 $a$ 的式子表示）；

(3)、若抛物线与 $x$ 轴相交于 $A ， B$ 两点，且 $A B \leq 4$ ，求 $a$ 的取值范围．

查看试题解析
27. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ C A B = 2 α$ ，在△ABC的外侧作直线 $A P (90 ° - a < ∠ P A C < 180 ° - 2 a)$ ，作点 $C$ 关于直线 $A P$ 的对称点 $D$ ，连接 $A D ， B D ， B D$ 交直线 $A P$ 于点 $E$ ．

(1)、依题意补全图形；

(2)、连接 $C E$ ，求证： $∠ A C E = ∠ A B E$ ；

(3)、过点 $A$ 作 $A F ⊥ C E$ 于点 $F$ ，用等式表示线段 $B E ， 2 E F ， D E$ 之间的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于图形 $G$ 及过定点 $P (3 ， 0)$ 的直线 $l$ ，有如下定义：过图形 $G$ 上任意一点 $Q$ 作 $Q H ⊥ l$ 于点 $H$ ，若 $Q H + P H$ 有最大值，那么称这个最大值为图形 $G$ 关于直线 $l$ 的最佳射影距离，记作 $d (G ， l)$ ，此时点 $Q$ 称为图形 $G$ 关于直线 $l$ 的最佳射影点．

(1)、如图1，已知 $A (2 ， 2)$ ， $B (3 ， 3)$ ，写出线段 $A B$ 关于 $x$ 轴的最佳射影距离 $d (A B ， x 轴) =$ ；

(2)、已知点 $C (3 ， 2)$ ， ⊙C的半径为 $\sqrt{2}$ ，求⊙C关于 $x$ 轴的最佳射影距离d（⊙C，x轴），并写出此时⊙C 关于 $x$ 轴的最佳射影点 $Q$ 的坐标；

(3)、直接写出点 $D (0 ， \sqrt{3})$ 关于直线 $l$ 的最佳射影距离 $d (点 D ， l)$ 的最大值．

查看试题解析

$x$	$\frac{1}{2}$	1	$\frac{3}{2}$	2	$\frac{5}{2}$	3	$\frac{7}{2}$	4	$\frac{9}{2}$	5
$y$	10	$\frac{13}{2}$	6	$a$	$\frac{34}{5}$	$\frac{15}{2}$	$\frac{58}{7}$	$\frac{73}{8}$	$b$	$\frac{109}{10}$