北京市大兴区2022年九年级中考二模数学试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022年北京冬奥会共录用了赛会志愿者18000多人，他们就像一朵朵热情洋溢的小雪花，在各自岗位上展现开放，阳光向上的风采．将18000用科学记数法表示应为（）

A、 $0.18 \times 1 0^{5}$ B、 $18 \times 1 0^{3}$ C、 $1.8 \times 1 0^{4}$ D、 $1.8 \times 1 0^{5}$

查看试题解析
2. 下图是某个几何体的三视图，该几何体是（）

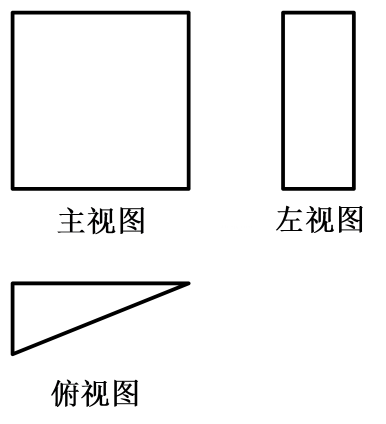A、长方体 B、正方体 C、圆柱 D、三棱柱

查看试题解析
3. 如果反比例函数 $y = \frac{k}{x}$ 的图象经过点 $P (- 4 ， 3)$ ，那么k的值是（）

A、-12 B、 $- \frac{4}{3}$ C、 $- \frac{3}{4}$ D、12

查看试题解析
4. 某男装专卖店老板专营母品牌夹克，店主统计了一周中不同尺码夹克销售情况如下表：

尺码

39

40

41

42

43

平均每天销售量

10

12

20

12

12

如果每件夹克的利润相同，你认为该店主最关注的销售数据是下列统计量中的（）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析
5. 下列图形中，是轴对称图形但不是中心对称图形的是（　　）

A、等边三角形 B、平行四边形 C、矩形 D、圆

查看试题解析
6. 如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD︰AB＝3︰4，AE＝6，则AC等于（）

A、3 B、4 C、6 D、8

查看试题解析
7. 如图，圆的两条弦AB，CD相交于点E，且 $\overset{⌢}{A D} = \overset{⌢}{C B} ， ∠ A = 40 °$ ，则 $∠ C E B$ 的度数为（）

A、50° B、80° C、70° D、90°

查看试题解析
8. 根据市场调查，某种消毒液的大瓶装（500克）和小瓶装（250克）两种产品的销售数量（按瓶计算）比为2∶5．某厂每天生产这种消毒液22500000克，这些清毒液应该分装大，小瓶两种产品各多少瓶?设这些消毒液应该分装大瓶x瓶，小瓶y瓶．依题意可列方程组为（）

A、 ${\begin{array}{l} 2 x = 5 y \\ 500 x + 250 y = 22500000 \end{array}$ B、 ${\begin{array}{l} 2 x = 5 y \\ 250 x + 500 y = 22500000 \end{array}$ C、 ${\begin{array}{l} 5 x = 2 y \\ 250 x + 500 y = 22500000 \end{array}$ D、 ${\begin{array}{l} 5 x = 2 y \\ 500 x + 250 y = 22500000 \end{array}$

查看试题解析

二、填空题

9. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
10. 请写出一个开口向下，对称轴为y轴的抛物线的解析式 $y =$ ．

查看试题解析
11. 若无理数a满足1<a<4，请你写出一个符合条件的无理数。

查看试题解析
12. 方程 $\frac{2}{x + 1} = \frac{1}{x}$ 的解为．

查看试题解析
13. 如图所示的网格是正方形网格，点A，B，P是网格线交点，则 $∠ P B A$ 与 $∠ P A B$ 的大小关系是： $∠ P B A$ $∠ P A B$ （填“>”，“=”或“<”）．

查看试题解析
14. 如图，▱ABCD中，AB=3，BC=5，AE平分∠BAD交BC于点E，则CE的长为．

查看试题解析
15. 如图，菱形ABCD的面积为12，其中对角线AC长为4，则对角线BD的长为．

查看试题解析
16. 某超市对某品牌袋装茶叶搞促销活动商家将该品牌袋装茶叶按以下五种类型出售：A类有一袋茶叶，B类有二袋茶叶，C类有三袋茶叶，D类有五袋茶叶，E类有七袋茶叶，价格如下表：
种类
A
B
C
D
E
单价（元/类）
20
36
42
65
90
小云准备在该超市购买6袋上述品牌的茶叶，则购买茶叶的总费用最低为元．

查看试题解析

三、解答题

17. 计算： $\sqrt{32} - 2 s i n 45 ° + {(2 - π)}^{0} - {(\frac{1}{4})}^{- 1}$

查看试题解析
18. 如图，已知直线 $y = k x + b$ 经过点 $(0 ， - 3)$ 和点M，求此直线与x轴的交点坐标．

查看试题解析
19. 已知： $x^{2} + 3 x = 1$ ，求代数式 $\frac{1}{x - 1} \cdot \frac{x^{2} - 2 x + 1}{x + 2} - \frac{x - 2}{x + 1}$ 的值.

查看试题解析
20. 下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程．
已知：直线l和直线l外一点P．
求作：直线PQ，使得 $P Q ∥ l$ ．
作法：如图，
①在直线l上任取两点A，B；
②以点P为圆心，AB长为半径画弧，以点B为圆心，AP长为半径画弧，两弧在直线l上方相交于点Q；
③作直线PQ．
直线PQ就是所求作的直线．
根据小东设计的尺规作图过程，

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：∵ $P A = Q B ， A B = P Q$ ，
∴四边形PABQ是平行四边形（）（填写推理的依据）．
∴ $P Q ∥ A B$ （）（填写推理的依据）．
即 $P Q ∥ l$

查看试题解析
21. 已知关于x的一元二次方程3x²﹣6x+1﹣k=0有实数根，k为负整数．

(1)、求k的值；

(2)、如果这个方程有两个整数根，求出它的根．

查看试题解析
22. 一次演讲比赛中，评委将从演讲内容，演讲能力，演讲效果三个方面为选手打分．各项成绩均按百分制计，然后再按演讲内容占50%，演讲能力占40%，演讲效果占10%，计算选手的综合成绩（百分制）．进入决赛的前两名选手的单项成绩和综合成绩如下表所示．
选手
演讲内容
演讲能力
演讲效果
综合成绩
A
85
95
95
m
B
95
85
95
91

(1)、求出m的值；

(2)、请根据综合成绩确定两人的名次．

查看试题解析
23. 一个滑雪者从山坡滑下，如果不计其他因素，经测量得到滑行距离y（单位：米）与滑行时间x（单位：秒）的数据（如下表）：
滑行时间x（秒）
0
0.5
1
1.5
2
2.5
3
3.5
4
…
58
滑行距离y（米）
0
1.2
2.6
4.4
6.4
8.8
11.4
14.4
17.6
…
2134.4
请解决以下问题：

(1)、如下图，在平面直角坐标系xOy中，根据表中数值描点 $(x ， y)$ ，请你用平滑曲线连接描出的这些点；

(2)、当滑雪者滑行3秒时，滑行距离是米；

(3)、下面三个推断：
①曲线上每一个点都代表x的值与y的值的一种对应
②自变量x的取值范围是 $x \geq 0$
③滑行最远距离是2134.4米
所有推断正确的序号是

查看试题解析
24. 如图，P是正方形ABCD对角线AC上一点，点E在BC上，且PE＝PB．

(1)、求证：PE＝PD；

(2)、求∠PED的度数．

查看试题解析
25. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， A D$ 是 $∠ B A C$ 的平分线，O是 $A B$ 上一点，以 $O A$ 为半径的 $⊙ O$ 经过点D．

(1)、求证： $B C$ 是 $⊙ O$ 的切线；

(2)、若 $B D = 5 ， D C = 3$ ，求 $A C$ 的长．

查看试题解析
26. 关于x的二次函数 $y_{1} = x^{2} + m x$ 的图象过点 $(- 2 ， 0)$ ．

(1)、求二次函数 $y_{1} = x^{2} + m x$ 的表达式；

(2)、已知关于x的二次函数 $y_{2} = - x^{2} + 2 x$ ，一次函数 $y_{3} = k x + b (k \neq 0)$ ，在实数范围内，对于x的同一个值，这三个函数所对应的函数值 $y_{1} \geq y_{3} \geq y_{2}$ 均成立．
①求b的值；
②直接写出k的值．

查看试题解析
27. 已知：如图， $A C = A B ， ∠ C A B = ∠ C D B = α$ ，线段CD与AB相交于点O，以点A为中心，将射线AD绕点A逆时针旋转 $α (0 < α < 180 °)$ 交线段CD于点H．

(1)、若 $α = 60 °$ ，求证： $C D = A D + B D$ ；

(2)、请你直接用等式表示出线段CD，AD，BD之间的数量关系（用含 $α$ 的式子表示）．

查看试题解析
28. 在平面直角坐标系xOy中，对于点P和直线 $y = 1$ ，给出如下定义：若点P在直线 $y = 1$ 上，且以点P为顶点的角是45°，则称点P为直线 $y = 1$ 的“关联点”．

(1)、若在直线 $x = 1$ 上存在直线 $y = 1$ 的“关联点”P．则点P的坐标为；

(2)、过点 $P (2 ， 1)$ 作两条射线，一条射线垂直于x轴，垂足为A；另一条射线、交x轴于点B，若点P为直线 $y = 1$ 的“关联点”．求点B的坐标；

(3)、以点O为圆心，1为半径作圆，若在 $⊙ O$ 上存在点N，使得 $∠ O P N$ 的顶点P为直线 $y = 1$ 的“关联点”．则点P的横坐标a的取值范围是．

查看试题解析

选手	演讲内容	演讲能力	演讲效果	综合成绩
A	85	95	95	m
B	95	85	95	91

滑行时间x（秒）	0	0.5	1	1.5	2	2.5	3	3.5	4	…	58
滑行距离y（米）	0	1.2	2.6	4.4	6.4	8.8	11.4	14.4	17.6	…	2134.4

尺码	39	40	41	42	43
平均每天销售量	10	12	20	12	12

种类	A	B	C	D	E
单价（元/类）	20	36	42	65	90