北京市朝阳区2022年中考二模数学试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 汉字是迄今为止持续使用时间最长的文字，是传承中华文化的重要载体．汉字在发展过程中演变出多种字体，给人以美的享受．下面是“北京之美”四个字的篆书，不能看作轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 2021年《中共中央国务院关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》发布，明确了我国实现碳达峰碳中和的时间表、路线图．文件提出到2030年森林蓄积量达到190亿立方米．将19000000000用科学记数法表示应为（）

A、 $19 \times 1 0^{10}$ B、 $1.9 \times 1 0^{10}$ C、 $0.19 \times 1 0^{11}$ D、 $1.9 \times 1 0^{9}$

查看试题解析
3. 实数a在数轴上的对应点的位置如图所示，若实数b满足 $a + b > 0$ ，则b的值可以是（）

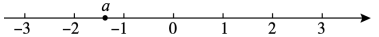A、－2 B、－1 C、1 D、2

查看试题解析
4. 如图，点C，D在直线AB上， $O C ⊥ O D$ ，若 $∠ A C O = 12 0^{∘}$ ，则∠BDO的大小为（）

A、 $12 0^{∘}$ B、 $14 0^{∘}$ C、 $15 0^{∘}$ D、 $16 0^{∘}$

查看试题解析
5. 从1，2，3这3个数中随机抽取两个数相加，和为偶数的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 在太阳光的照射下，一个矩形框在水平地面上形成的投影不可能是（）

A、 B、 C、 D、

查看试题解析
7. 9个互不相等的数组成了一组数据，其平均数a与这9个数都不相等．把a和这9个数组成一组新的数据，下列结论正确的是（）

A、这两组数据的平均数一定相同 B、这两组数据的方差一定相同 C、这两组数据的中位数可能相同 D、以上结论都错误

查看试题解析
8. 用绳子围成周长为10m的正x边形，记正x边形的边长为ym，内角和为 $S^{∘}$ ．当x在一定范围内变化时，y和S都随着x的变化而变化，则y与x，S与x满足的函数关系分别是（）

A、一次函数关系，二次函数关系 B、一次函数关系，反比例函数关系 C、反比例函数关系，二次函数关系 D、反比例函数关系，一次函数关系

查看试题解析

二、填空题

9. 若 $\sqrt{x + 3}$ 在实数范围内有意义，则x的取值范围为．

查看试题解析
10. 分解因式： $2 m^{2} - 2 n^{2} =$ ．

查看试题解析
11. 若关于x的一元二次方程 $x^{2} - 4 x + m - 1 = 0$ 有两个不相等的实数根，则m的取值范围是．

查看试题解析
12. 如图，AB是⊙O的直径，点C在⊙O上， $∠ A B C = 7 0^{∘}$ ， PA，PC是⊙O的切线．∠P＝°．

查看试题解析
13. 如图，OP平分∠MON，过点P的直线与OM，ON分别相交于点A、B，只需添加一个条件即可证明 $Δ A O P ≅ Δ B O P$ ，这个条件可以是（写出一个即可）．

查看试题解析
14. 如图所示的网格是正方形网格，网格中三条线段的端点均是格点，以这三条线段为边的三角形是三角形（填“锐角”、“直角”或“钝角”）．

查看试题解析
15. 在平面直角坐标系xOy中，若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象与直线 $x = 1$ 的交点的纵坐标为2，则该图象与直线 $y = - 2$ 的交点的横坐标为．

查看试题解析
16. 围棋是一种起源于中国的棋类游戏，在春秋战国时期即有记载，围棋棋盘由横纵各19条等距线段构成，围棋的棋子分黑白两色，下在横纵线段的交叉点上．若一个白子周围所有相邻（有线段连接）的位置都有黑子，白子就被黑子围住了．如图1，围住1个白子需要4个黑子，固住2个白子需要6个黑子，如图2，围住3个白子需要8个或7个黑子，像这样，不借助棋盘边界，只用15个黑子最多可以围住个白子．

查看试题解析

三、解答题

17. 计算 $\sqrt{18} + 2 s i n 4 5^{∘} - {(\frac{1}{2})}^{- 1} + | \sqrt{2} - 2 |$ ．

查看试题解析
18. 解分式方程： $\frac{x}{x - 2} - \frac{3}{2 x - 4} = \frac{1}{2}$ ．

查看试题解析
19. 解不等式 $x - 5 < \frac{x - 12}{3}$ ，并写出它的所有非负整数解．

查看试题解析
20. 在平面直角坐标系xOy中，一次函数 $y = k x + b (k \neq 0)$ 的图象由函数 $y = 2 x$ 的图象平移得到，且经过点（2，2）．

(1)、求这个一次函数的表达式；

(2)、当 $x < 2$ 时，对于x的每一个值，函数 $y = m x (m \neq 0)$ 的值大于一次函数 $y = k x + b$ 的值，直接写出m的取值范围．

查看试题解析
21. 已知：线段AB．
求作：△ABC，使得 $∠ A = 9 0^{∘}$ ， $∠ C = 3 0^{∘}$ ．
作法：①分别以点A，B为圆心，AB长为半径画弧，在直线AB的一侧相交于点D；
②连接BD并延长，在BD的延长线上取一点C，使得 $C D = B D$ ；
③连接AC．
△ABC就是所求作的三角形．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接AD．
∵ $A B = B D = A D$ ，
∴△ABD是等边三角形（ ① ）（填推理的依据）．
∴ $∠ B = ∠ A D B = 6 0^{∘}$ ．
∵ $C D = B D$ ，
∴ $C D = A D$ ．
∴ $∠ D A C = ∠ A C B$ ．
∴ $∠ A D B = ∠ D A C + ∠ A C B$ （ ② ）（填推理的依据）
$= 2 ∠ A C B$ ．
∴ $∠ A C B = 3 0^{∘}$ ．
∴ $∠ B A C = 9 0^{∘}$ ．

查看试题解析
22. 如图，在菱形ABCD中，O为AC，BD的交点，P，M，N分别为CD，OD，OC的中点．

(1)、求证：四边形OMPN是矩形；

(2)、连接AP，若 $A B = 4$ ， $∠ B A D = 6 0^{∘}$ ，求AP的长．

查看试题解析
23. 如图，AB为⊙O的直径，C为⊙O上的一点， $O D ⊥ A B$ 交AC于点E， $D E = D C$ ．

(1)、求证：DC是⊙O的切线；

(2)、若 $O A = 4$ ， $O E = 2$ ，求cosD．

查看试题解析
24. 某公园在垂直于湖面的立柱上安装了一个多孔喷头，从喷头每个孔喷出的水柱形状都相同，可以看作是抛物线的一部分，当喷头向四周同时喷水时，形成一个环状喷泉，安装后，通过测量其中一条水柱，获得如下数据，在距立柱水平距离为d米的地点，水柱距离湖面的高度为h米，
请解决以下问题：
d（米）
0
1.0
3.0
5.0
7.0
h（米）
3.2
4.2
5.0
4.2
1.8

(1)、在网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；

(2)、结合表中所给数据或所画图象，直接写出这条水柱最高点距离湖面的高度；

(3)、求所画图象对应的函数表达式；

(4)、从安全的角度考虑，需要在这个喷泉外围设立一圈正方形护栏，这个喷泉的任何一条水柱在湖面上的落点到护栏的距离不能小于1米，请通过计算说明公园至少需要准备多少米的护栏（不考虑接头等其他因素）．

查看试题解析
25. 某年级共有300名学生，为了解该年级学生A，B两门课程的学习情况，从中随机抽取30名学生进行测试，获得了他们的成绩（百分制），并对数据（成绩）进行整理、描述和分析，相关信息如下：
α.30名学生A，B两门课程成绩统计图：
b.30名学生A，B两门课程成绩的平均数如下：

A课程
B课程
平均数
85.1
80.6
根据以上信息，回答下列问题：

(1)、在这30名学生中，甲同学A课程成绩接近满分，B课程成绩没有达到平均分，请在图中用“○”圈出代表甲同学的点；

(2)、这30名学生A课程成绩的方差为 $s_{1}^{2}$ ， B课程成绩的方差为 $s_{2}^{2}$ ，直接写出 $s_{1}^{2}$ ， $s_{2}^{2}$ 的大小关系；

(3)、若该年级学生都参加此次测试，估计A，B两门课程成绩都超过平均分的人数．

查看试题解析
26. 在平面直角坐标系xOy中，已知抛物线 $y = x^{2} + (a + 2) x + 2 a$ ．

(1)、求抛物线的对称轴（用含a的式子表示）；

(2)、若点（－1， $y_{1}$ ），（a， $y_{2}$ ），（1， $y_{3}$ ）在抛物线上，且 $y_{1} < y_{2} < y_{3}$ ，求a的取值范围．

查看试题解析
27. 在正方形ABCD中，E为BC上一点，点M在AB上，点N在DC上，且 $M N ⊥ D E$ ，垂足为点F．

(1)、如图1，当点N与点C重合时，求证： $M N = D E$ ；

(2)、将图1中的MN向上平移，使得F为DE的中点，此时MN与AC相交于点H，
①依题意补全图2；
②用等式表示线段MH、HF，FN之间的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系xOy中，⊙O的半径为1， $A B = 1$ ，且A，B两点中至少有一点在⊙O外．给出如下定义：平移线段AB，得到线段 $A^{'} B^{'}$ （ $A^{'}$ ， $B^{'}$ 分别为点A，B的对应点），若线段 $A^{'} B^{'}$ 上所有的点都在⊙O的内部或⊙O上，则线段 $A A^{'}$ 长度的最小值称为线段AB到⊙O的“平移距离”．

(1)、如图1，点 $A_{1}$ ， $B_{1}$ 的坐标分别为（－3，0），（－2，0），线段 $A_{1} B_{1}$ 到⊙O的“平移距离”为，点 $A_{2}$ ， $B_{2}$ 的坐标分别为（－ $\frac{1}{2}$ ， $\sqrt{3}$ ），（ $\frac{1}{2}$ ， $\sqrt{3}$ ），线段 $A_{2} B_{2}$ 到⊙O的“平移距离”为；

(2)、若点A，B都在直线 $y = \sqrt{3} x + 2 \sqrt{3}$ 上，记线段AB到⊙O的“平移距离”为d，求d的最小值；

(3)、如图2，若点A坐标为（1， $\sqrt{3}$ ），线段AB到⊙O的“平移距离”为1，画图并说明所有满足条件的点B形成的图形（不需证明）．

查看试题解析

d（米）	0	1.0	3.0	5.0	7.0
h（米）	3.2	4.2	5.0	4.2	1.8

	A课程	B课程
平均数	85.1	80.6