广东省深圳市2023届高三数学第一次调研试题

试卷更新日期：2023-03-09 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知i为虚数单位， $(1 + i) z = 2$ ，则 $z =$ （）

A、 $1 + i$ B、 $1 - i$ C、 $- 1 + i$ D、 $- 1 - i$

查看试题解析
2. 满足等式 ${0 ， 1} \cup X = {x \in R | x^{3} = x}$ 的集合X共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 已知 $f (x)$ 为奇函数，且 $x < 0$ 时， $f (x) = e^{x}$ ，则 $f (e) =$ （）

A、 $e^{e}$ B、 $- e^{e}$ C、 $e^{- e}$ D、 $- e^{- e}$

查看试题解析
4. 如图，一个棱长1分米的正方体形封闭容器中盛有V升的水，若将该容器任意放置均不能使水平面呈三角形，则V的取值范围是（）

A、 $(\frac{1}{6} ， \frac{5}{6})$ B、 $(\frac{1}{3} ， \frac{2}{3})$ C、 $(\frac{1}{2} ， \frac{2}{3})$ D、 $(\frac{1}{6} ， \frac{1}{2})$

查看试题解析
5. 已知 $\vec{a}$ ， $\vec{b}$ 为单位向量，且 $| 3 \vec{a} - 5 \vec{b} | = 7$ ，则 $\vec{a}$ 与 $\vec{a} - \vec{b}$ 的夹角为（）

A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、 $\frac{π}{6}$ D、 $\frac{5 π}{6}$

查看试题解析
6. 将一个顶角为120°的等腰三角形（含边界和内部）的底边三等分，挖去由两个等分点和上顶点构成的等边三角形，得到与原三角形相似的两个全等三角形，再对余下的所有三角形重复这一操作．如果这个操作过程无限继续下去…，最后挖剩下的就是一条“雪花”状的Koch曲线，如图所示已知最初等腰三角形的面积为1，则经过4次操作之后所得图形的面积是（）

A、 $\frac{16}{81}$ B、 $\frac{20}{81}$ C、 $\frac{8}{27}$ D、 $\frac{10}{27}$

查看试题解析
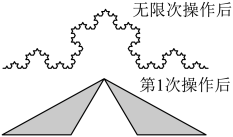7. 安排5名大学生到三家企业实习，每名大学生只去一家企业，每家企业至少安排1名大学生，则大学生甲、乙到同一家企业实习的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{3}{10}$ C、 $\frac{3}{25}$ D、 $\frac{6}{25}$

查看试题解析
8. 已知函数 $f (x) = 2 + l n x$ ， $g (x) = a \sqrt{x}$ ，若总存在两条不同的直线与函数 $y = f (x)$ ， $y = g (x)$ 图象均相切，则实数a的取值范围为（）

A、 $(0 ， 1)$ B、 $(0 ， 2)$ C、 $(1 ， 2)$ D、 $(1 ， e)$

查看试题解析

二、多选题

9. 已知函数 $f (x)$ 的图象是由函数 $y = 2 s i n x c o s x$ 的图象向右平移 $\frac{π}{6}$ 个单位得到，则（）

A、 $f (x)$ 的最小正周期为π B、 $f (x)$ 在区间 $[- \frac{π}{6} ， \frac{π}{3}]$ 上单调递增 C、 $f (x)$ 的图象关于直线 $x = \frac{π}{3}$ 对称 D、 $f (x)$ 的图象关于点 $(\frac{π}{6} ， 0)$ 对称

查看试题解析
10. 已知抛物线C： $y^{2} = 2 x$ 的准线为 $l$ ，直线 $x = m y + n$ 与C相交于A、B两点，M为AB的中点，则（）

A、当 $n = \frac{1}{2}$ 时，以AB为直径的圆与 $l$ 相交 B、当 $n = 2$ 时，以AB为直径的圆经过原点O C、当 $| A B | = 4$ 时，点M到 $l$ 的距离的最小值为2 D、当 $| A B | = 1$ 时，点M到 $l$ 的距离无最小值

查看试题解析
11. 已知函数 $f (x) = x {(x - 3)}^{2}$ ，若 $f (a) = f (b) = f (c)$ ，其中 $a < b < c$ ，则（）

A、 $1 < a < 2$ B、 $a + b + c = 6$ C、 $a + b > 2$ D、abc的取值范围是 $(0 ， 4)$

查看试题解析
12. 如图，已知正三棱台 $A B C - A_{1} B_{1} C_{1}$ 的上、下底面边长分别为2和3，侧棱长为1，点P在侧面 $B C C_{1} B_{1}$ 内运动（包含边界），且AP与平面 $B C C_{1} B_{1}$ 所成角的正切值为 $\sqrt{6}$ ，则（）

A、CP长度的最小值为 $\sqrt{3} - 1$ B、存在点P，使得 $A P ⊥ B C$ C、存在点P，存在点 $Q \in B_{1} C_{1}$ ，使得 $A P ∥ A_{1} Q$ D、所有满足条件的动线段AP形成的曲面面积为 $\frac{\sqrt{7} π}{3}$

查看试题解析

三、填空题

13. ${(1 - x)}^{5}$ 的展开式中 $x^{3}$ 的系数为（用数字做答）．

查看试题解析
14. 若椭圆上的点到焦点距离的最大值是最小值的2倍，则该椭圆的离心率为．

查看试题解析
15. 定义开区间 $(a ， b)$ 的长度为 $b - a$ ．经过估算，函数 $f (x) = \frac{1}{2^{x}} - x^{\frac{1}{3}}$ 的零点属于开区间（只要求写出一个符合条件，且长度不超过 $\frac{1}{6}$ 的开区间）．

查看试题解析
16. 设 $a > 0$ ， $A (2 a ， 0)$ ， $B (0 ， 2)$ ， O为坐标原点，则以 $O A$ 为弦，且与AB相切于点A的圆的标准方程为；若该圆与以OB为直径的圆相交于第一象限内的点P（该点称为直角△OAB的Brocard点），则点P横坐标x的最大值为．

查看试题解析

四、解答题

17. 记 $S_{n}$ ，为数列 ${a_{n}}$ 的前n项和，已知 $S_{n} = \frac{a_{n}}{2} + n^{2} + 1$ ， $n \in N^{*}$ ．

(1)、求 $a_{1} + a_{2}$ ，并证明 ${a_{n} + a_{n + 1}}$ 是等差数列；

(2)、求 $S_{n}$ ．

查看试题解析
18. 记 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，已知 $b + c = 2 a s i n (C + \frac{π}{6})$ ．

(1)、求 $A$ ；

(2)、设 $A B$ 的中点为 $D$ ，若 $C D = a$ ，且 $b - c = 1$ ，求 $△ A B C$ 的的面积．

查看试题解析
19. 如图，在四棱锥P-ABCD中， $P D ⊥ A B$ ，且 $P D = P B$ ，底面ABCD是边长为2的菱形， $∠ B A D = \frac{π}{3}$ ．

(1)、证明：平面PAC⊥平面ABCD；

(2)、若 $P A ⊥ P C$ ，求平面PAB与平面PBC夹角的余弦值．

查看试题解析
20. 某企业因技术升级，决定从2023年起实现新的绩效方案．方案起草后，为了解员工对新绩效方案是否满意，决定采取如下“随机化回答技术”进行问卷调查：
一个袋子中装有三个大小相同的小球，其中1个黑球，2个白球．企业所有员工从袋子中有放回的随机摸两次球，每次摸出一球．约定“若两次摸到的球的颜色不同，则按方式Ⅰ回答问卷，否则按方式Ⅱ回答问卷”．
方式Ⅰ：若第一次摸到的是白球，则在问卷中画“○”，否则画“×”；
方式Ⅱ：若你对新绩效方案满意，则在问卷中画“○”，否则画“×”．
当所有员工完成问卷调查后，统计画○，画×的比例．用频率估计概率，由所学概率知识即可求得该企业员工对新绩效方案的满意度的估计值．其中满意度 $= \frac{企业所有对新绩效方案满意的员工人数}{企业所有员工人数} \times 100 %$ ．

(1)、若该企业某部门有9名员工，用X表示其中按方式Ⅰ回答问卷的人数，求X的数学期望；

(2)、若该企业的所有调查问卷中，画“○”与画“×”的比例为4：5，试估计该企业员工对新绩效方案的满意度．

查看试题解析
21. 已知双曲线E： $\frac{x^{2}}{4} - y^{2} = 1$ 与直线l： $y = k x - 3$ 相交于A、B两点，M为线段AB的中点．

(1)、当k变化时，求点M的轨迹方程；

(2)、若l与双曲线E的两条渐近线分别相交于C、D两点，问：是否存在实数k，使得A、B是线段CD的两个三等分点？若存在，求出k的值；若不存在，说明理由．

查看试题解析
22. 已知函数 $f (x) = \frac{a (x + 4)}{e^{x}}$ ，其中 $a \in R$ 且 $a \neq 0$ ．

(1)、当 $a = 1$ 时，求函数 $f (x)$ 的单调区间；

(2)、若存在实数 $x_{0}$ ，使得 $f (x_{0}) = x_{0}$ ，则称 $x_{0}$ 为函数 $f (x)$ 的“不动点”求函数 $f (x)$ 的“不动点”的个数；

(3)、若关于x的方程 $f (f (x)) = f (x)$ 有两个相异的实数根，求a的取值范围．

查看试题解析