人教版八年级下数学疑难点专题专练——16.1二次根式

试卷更新日期：2023-03-09 类型：同步测试

进入出卷网下载

一、单选题

1. 要使式子 $\frac{3}{\sqrt{6 - 2 x}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x < 3$ B、 $x \geq 3$ C、 $x \leq 3$ D、 $x \neq 3$

查看试题解析
2. 若式子 $\frac{\sqrt{x + 2}}{x - 1}$ 有意义，则实数x的取值范围是（）．

A、 $x \geq - 2$ 且 $x \neq 1$ B、 $x \neq 1$ C、 $x > 1$ D、 $x \geq - 2$

查看试题解析
3. 在函数 $y = \frac{\sqrt{x - 1}}{x - 2}$ 中，自变量x的取值范围是（）

A、 $x \geq 1$ B、 $x > 1$ C、 $x \geq 1$ 且 $x \neq 2$ D、 $x > 1$ 且 $x \neq 2$

查看试题解析
4. 函数 $y = \frac{\sqrt{x}}{x - 1}$ 的自变量x的取值范围是（）

A、 $x > 0$ B、 $x \neq 1$ C、 $x > 1 且 x \neq 1$ D、x≥0且x≠1

查看试题解析
5. 若代数式 $\frac{\sqrt{x + 1}}{(x - 3)^{2}}$ 有意义，则实数x的取值范围是（）

A、 $x \geq - 1$ B、 $x \geq - 1$ 且 $x \neq 3$ C、 $x > - 1$ D、 $x > - 1$ 且 $x \neq 3$

查看试题解析
6. 函数 $y = \frac{\sqrt{x + 2}}{x^{2} - 9}$ 的自变量x的取值范围是（）

A、x≠±3 B、x≤﹣2 C、x≠3 D、x≥﹣2且x≠3

查看试题解析
7. 已知 $\sqrt{x^{2} - 10 x + 25}$ ＝5﹣x，则x的取值范围是（）

A、为任意实数 B、0≤x≤5 C、x≥5 D、x≤5

查看试题解析
8. 式子 $\sqrt{2 - x} + \frac{1}{x + 1}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \leq 2$ B、 $x \leq 2$ 且 $x \neq - 1$ C、 $x \geq 2$ D、 $x \geq 2$ 且 $x \neq - 1$

查看试题解析
9. 已知 $1 < x < 2$ ，则 $| x - 3 | + \sqrt{{(x - 2)}^{2}}$ 的值为（）

A、 $2 x - 5$ B、－2 C、 $5 - 2 x$ D、2

查看试题解析
10. 实数a，b在数轴上的位置如图所示，则化简 $\sqrt{a^{2}} - \sqrt{b^{2}} - \sqrt{(a - b)^{2}}$ 的结果是（）

A、 $- 2 b$ B、 $- 2 a$ C、 $2 b - 2 a$ D、0

查看试题解析
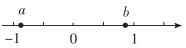11. 若 $\sqrt{80 m}$ 是正整数，则满足条件的m的最小正整数值为（）

A、5 B、6 C、7 D、8

查看试题解析
12. 若化简 $| 1 - x | - \sqrt{x^{2} - 8 x + 16}$ 的结果为 $2 x - 5$ ，则 $x$ 的取值范围是（）

A、 $x$ 为任意实数 B、 $1 \leq x \leq 4$ C、 $x \geq 1$ D、 $x \leq 4$

查看试题解析
13. 若代数式 $\sqrt{- m} + \frac{1}{\sqrt{m n}}$ 有意义，那么直角坐标系中点P（m，n）的位置在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
14. 已知 $a$ 满足 $| 2021 - a | + \sqrt{a - 2022} = a$ ，则 $a - 2021^{2} = （）$

A、0 B、1 C、2021 D、2022

查看试题解析

二、填空题

15. 如果y＝ $\sqrt{5 - x} + \sqrt{x - 5}$ +2，那么x^y的值是．

查看试题解析
16. 要使 $n$ 和 $\sqrt{45 n}$ 都是正整数，则 $n$ 最小为．

查看试题解析
17. 已知 $\sqrt{20 n}$ 是整数，则满足条件的最小整数n为．

查看试题解析
18. 已知 $a$ ， $b$ ， $c$ 实数在数轴上的对应点如图所示，化简 $\sqrt{a^{2}} - | c - a | + \sqrt{{(b - c)}^{2}} =$ ．

查看试题解析
19. 若x、y都为实数，且 $y = 2022 \sqrt{x - 4} + 2022 \sqrt{4 - x} + 9$ ，则 $x y$ 的值.

查看试题解析
20. 若代数式 $\frac{\sqrt{m + 1}}{\sqrt{m - 1}}$ 有意义，则 $m$ 的取值范围是.

查看试题解析
21. 如果式子 $\frac{\sqrt{1 - x}}{\sqrt{2 + x}}$ 有意义，那么 $x$ 的取值范围是．

查看试题解析
22. 若 $\sqrt{x - 2023} + | 2022 - x | = x$ ，则 $2022^{2} - x =$ .

查看试题解析
23. 实数a，b在数轴上对应点的位置如图所示，化简 $| a - b | + \sqrt{b^{2}}$ 的结果是（用代数式表示）

查看试题解析
24. 若 $\sqrt{24 N}$ 是正整数，则N的最小整数值是．

查看试题解析
25. 若 $\sqrt{12 - n}$ 是整数，则满足条件的自然数n可以是(写出一个即可)

查看试题解析

三、解答题

26. 已知 $y = \sqrt{x - 2} + \sqrt{2 - x} + \frac{3}{8}$ ，求 $\sqrt{x y}$ 的值．

查看试题解析
27. 已知实数x、y满足， $y = \frac{\sqrt{x^{2} - 4} + \sqrt{4 - x^{2}}}{x - 2} + 3$ ，求9x＋8y的值.

查看试题解析

四、综合题

28. 阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如： $3 + 2 \sqrt{2} = (1 + \sqrt{2})^{2}$ ，善于思考的小明进行了以下探索：
设 $a + b \sqrt{2} = (m + n \sqrt{2})^{2}$ （其中 $a ， b ， m ， n$ 均为整数），则有 $a + b \sqrt{2} = m^{2} + 2 n^{2} + 2 m n \sqrt{2}$ . $∴ a = m^{2} + 2 n^{2} ， b = 2 m n$ .这样小明就找到了一种把部分 $a + b \sqrt{2}$ 的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题：

(1)、当 $a ， b ， m ， n$ 均为正整数时，若 $a + b \sqrt{3} = (m + n \sqrt{3})^{2}$ ，用含 $m ， n$ 的式子分别表示 $a ， b$ ，得 $a =$ ， $b =$ ；

(2)、若 $a + 4 \sqrt{3} = (m + n \sqrt{3})^{2}$ ，且 $a ， m ， n$ 均为正整数，求 $a$ 的值.

查看试题解析
29. 有这样一类题目：将 $\sqrt{a + 2 \sqrt{b}}$ 化简，若你能找到两个数 $m$ 和 $n$ ，使 $m^{2} + n^{2} = a$ 且 $m n = \sqrt{b}$ ，则 $a + 2 \sqrt{b}$ 可变为 $m^{2} + n^{2} + 2 m n$ ，即变成 ${(m + n)}^{2}$ ，从而使得 $\sqrt{a + 2 \sqrt{b}}$ 化简.
例如： $∵ 5 + 2 \sqrt{6} = 3 + 2 + 2 \sqrt{6} = {(\sqrt{3})}^{2} + {(\sqrt{2})}^{2} + 2 \sqrt{6} = {(\sqrt{3} + \sqrt{2})}^{2}$

$∴ \sqrt{5 + 2 \sqrt{6}} = \sqrt{{(\sqrt{3} + \sqrt{2})}^{2}} = \sqrt{3} + \sqrt{2}$

请你仿照上例将下列各式化简：

(1)、 $\sqrt{4 + 2 \sqrt{3}}$ ；

(2)、 $\sqrt{7 - 2 \sqrt{10}}$ .

查看试题解析
30. 问题探究：因为 $(\sqrt{2} - 1)^{2} = 3 - 2 \sqrt{2}$ ，所以 $\sqrt{3 - 2 \sqrt{2}} = \sqrt{2} - 1 ，$
因为 $(\sqrt{2} + 1)^{2} = 3 + 2 \sqrt{2}$ ，所以 $\sqrt{3 + 2 \sqrt{2}} = \sqrt{2} + 1 ，$ 因为 $(2 - \sqrt{3})^{2} = 7 - 4 \sqrt{3}$ ，所以 $\sqrt{7 - 4 \sqrt{3}} = 2 - \sqrt{3} ，$ 请你根据以上规律，结合你的经验化简下列各式：

(1)、 $\sqrt{5 - 2 \sqrt{6}}$ ；

(2)、 $\sqrt{\frac{9}{4} + \sqrt{2}} \cdot$

查看试题解析