2022-2023学年初数北师大版八年级下册第三章图形的平移与旋转全章测试卷

试卷更新日期：2023-03-08 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC，若AB=10，BC=6．则线段BE的长为（）

A、10 B、12 C、14 D、16

查看试题解析
4. 在平面直角坐标系中，将点P （−x，1−x）先向右平移3个单位得点P₁ ，再将P₁向下平移3个单位得点P₂ ，若点P₂落在第四象限，则x的取值范围是（）

A、 $x > 3$ B、 $- 2 < x < 3$ C、 $x < - 2$ D、 $x < - 2$ 或 $x > 3$

查看试题解析
5. 在平面直角坐标系中，线段AB的两个端点分别是 $A (- 3 ， 2)$ ， $B (2 ， 1)$ ，将线段AB平移后，得到线段 $A^{'} B^{'}$ ，点 $B ′$ 的坐标为 $(- 2 ， 3)$ ，则点 $A ′$ 的坐标为（）

A、 $(1 ， 0)$ B、 $(1 ， 4)$ C、 $(- 7 ， 0)$ D、 $(- 7 ， 4)$

查看试题解析
6. 下列图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，在平面直角坐标系中，等边△OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（）

A、（4，2 $\sqrt{3}$ ） B、（3，3） C、（4，3） D、（3，2）

查看试题解析
8. 许多数学符号蕴含着对称美，在下列数学符号中，既是轴对称图形，又是中心对称图形的符号是（）

A、 B、 C、 D、

查看试题解析
9. 以图（1）（以O为圆心，半径为1的半圆）作为“基本图形”，分别经历如下变换，不能得到图（2）的是（）

A、绕着OB的中点旋转180°即可 B、先绕着点O旋转180°，再向右平移1个单位 C、先以直线AB为对称轴进行翻折，再向右平移1个单位 D、只要向右平移1个单位

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 60 °$ ， $A C = 1$ ，将 $△ A B C$ 绕点C按逆时针方向旋转得到 $△ A^{'} B^{'} C$ ，此时点 $A^{'}$ 恰好在 $A B$ 边上，则点 $B^{'}$ 与点B之间的距离为（）

A、2 B、3 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析

二、填空题(每题3分，共24分）

11. 如图，将△ABC绕着点C顺时针方向旋转50°后得到 $Δ A' B' C$ ．若 $∠ A = 40 °$ ， $∠ B = 110 °$ ，则 $∠ B C A'$ 的度数是．

查看试题解析
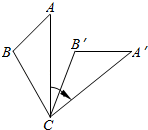12. 如图，网格中每个小正方形的边长均为1个单位长度，点A，B都在格点上.线段AB绕着某一定点顺时针旋转一个角度 $α (0 ° < α < 180 °)$ 后，得到线段A'B'（点A'，B'分别是A，B的对应点），则α的大小是.

查看试题解析
13. 如果将点A（-3，-1）向右平移2个单位长度，再向下平移3个单位得到点B，那么点B的坐标是．

查看试题解析
14. △ABC的三个顶点坐标分别是 $A (a ， 5)$ ， $B (7 ， b)$ ， $C (4 ， 9)$ ，将△ABC平移后得到 $△ A_{1} B_{1} C_{1}$ ，其中 $A_{1} (3 ， 8)$ ， $B_{1} (6 ， 3)$ ，则点 $C_{1}$ 的坐标是．

查看试题解析
15. 夏季荷花盛开，为了便于游客领略“人从桥上过，如在河中行”的美好意境，某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为300m，且桥宽忽略不计，则小桥总长为m.

查看试题解析
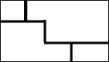16. 如图，将周长为8的 $△ A B C$ 沿 $B C$ 方向向右平移1.5个单位得到 $△ D E F$ ，则四边形 $A B F D$ 的周长为．

查看试题解析
17. 如图，在平面直角坐标系xOy中，点A的坐标为（2，0），点B在第一象限角平分线上，且BA⊥x轴，现将点A、B绕点O同时逆时针匀速旋转，当点A绕点O旋转90°到达y轴上的点C时，点B刚好绕点O旋转了45°到达y轴上的点D'处．则当点A旋转一周回到（2，0）时，点B所在的位置坐标为．

查看试题解析
18. 如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α.以OC为一边作等边三角形OCD，连接AD，当△AOD是等腰三角形时，求α的角度为

查看试题解析

三、综合题（共7题，共66分）

19. 如图所示的“钻石”型网格（由边长都为1个单位长度的等边三角形组成），其中已经涂黑了3个小三角形（阴影部分表示），请你再只涂黑一个小三角形，使它与阴影部分合起来所构成的完整图形是一个轴对称图形

(1)、画出其中一种涂色方式并画出此时的对称轴；

(2)、满足题意的涂色方式有种.

查看试题解析
20. 如图，△ABC中，AB=AC，∠BAC=36°.将△ABC绕点A顺时针旋转α（0°<α<180°）得到△ADE，BD，CE交于点F.

(1)、求证：△AEC≌△ADB；

(2)、求∠CFB的度数.

查看试题解析
21. 如图，在平面直角坐标系中，已知 $△ A B C$ 的三个顶点坐标分别是 $A (1 ， 1)$ ， $B (4 ， 1)$ ， $C (3 ， 3)$ .

(1)、将 $△ A B C$ 向下平移5个单位后得到 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、将 $△ A B C$ 绕原点 $O$ 逆时针旋转 $90 °$ 后得到 $△ A_{2} B_{2} C_{2}$ ，请画出 $△ A_{2} B_{2} C_{2}$ ；

(3)、判断以 $O$ ， $A_{1}$ ， $B$ 为顶点的三角形的形状并说明理由.

查看试题解析
22. 如图，在平面直角坐标系中， $△ A B C$ 三个顶点坐标分别为： $A (1 ， - 4)$ ， $B (5 ， - 4)$ ， $C (4 ， - 1)$ .

(1)、将 $△ A B C$ 经过平移得到 $△ A_{1} B_{1} C_{1}$ ，若点 $C$ 的应点 $C_{1}$ 的坐标为（2，5），则点 $A$ ， $B$ 的对应点 $A_{1}$ ， $B_{1}$ 的坐标分别为；

(2)、在如图的坐标系中画出 $△ A_{1} B_{1} C_{1}$ ，并画出与 $△ A_{1} B_{1} C_{1}$ 关于原点 $O$ 成中心对称的 $△ A_{2} B_{2} C_{2}$ .

(3)、在坐标系中画出 $△ A_{1} B_{1} C_{1}$ 绕点 $O$ 逆时针旋转90度后所得 $△ A_{3} B_{3} C_{3}$ ，则 $C_{3}$ 的坐标为.

查看试题解析
23. 如图，E是正方形ABCD的边CD上一点，以点A为中心．把△ADE绕点A逆时针旋转90°，得△ $A D^{'} E^{'}$ ，连接 $E E^{'}$ ．

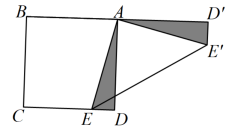(1)、 $∠ E A E^{'}$ 的度数为；

(2)、若AD＝4，DE＝1，求 $E E^{'}$ 的长．

查看试题解析
24. 如图，将△ABC沿BC的方向平移得到△DEF．

(1)、若∠B＝74°，∠F＝26°，求∠A的度数；

(2)、若BC＝3cm，EC＝2cm，求△ABC平移的距离．

查看试题解析
25. 图1，图2都是由边长为1的小等边三角形构成的网格，每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中，分别按下列要求选取一个涂上阴影：

(1)、使得4个阴影小等边三角形组成一个轴对称图形.

(2)、使得4个阴影小等边三角形组成一个中心对称图形.（请将两个小题依次作答在图1，图2中，均只需画出符合条件的一种情形）

查看试题解析

2022-2023学年初数北师大版八年级下册 第三章 图形的平移与旋转 全章测试卷

一、单选题（每题3分，共30分）

二、填空题(每题3分，共24分）

三、综合题（共7题，共66分）

2022-2023学年初数北师大版八年级下册第三章图形的平移与旋转全章测试卷