2022-2023学年初数北师大版八年级下册 3.2 图形的旋转 同步必刷题
试卷更新日期:2023-03-08 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 将图中可爱的“小鸭子”图片按逆时针方向旋转90°后得到的图片是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,在平面直角坐标系中,点A的坐标为 , 将点A烧原点O逆时针方向旋转得到点B,则点B的坐标为( )
2. 如图,在平面直角坐标系中,点A的坐标为 , 将点A烧原点O逆时针方向旋转得到点B,则点B的坐标为( ) A、 B、 C、 D、3. 如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,∠ACB=22°,则∠ADC=( )
A、 B、 C、 D、3. 如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,∠ACB=22°,则∠ADC=( )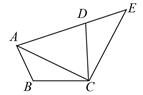 A、57° B、62° C、67° D、72°4. 如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )
A、57° B、62° C、67° D、72°4. 如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )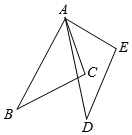 A、10° B、15° C、20° D、25°5. 如图,正方形ABCD中,点O为对角线的交点,直线EF过点O分别交AB、CD于E、F两点(BE>EA),若过EF上异于点O的一点作直线与正方形的一组对边所在的直线分别交于G、H两点,满足GH=EF,则这样的直线GH(不同于直线EF)的条数共有( )
A、10° B、15° C、20° D、25°5. 如图,正方形ABCD中,点O为对角线的交点,直线EF过点O分别交AB、CD于E、F两点(BE>EA),若过EF上异于点O的一点作直线与正方形的一组对边所在的直线分别交于G、H两点,满足GH=EF,则这样的直线GH(不同于直线EF)的条数共有( )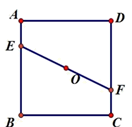 A、1条 B、2条 C、3条 D、无数条6. 如图,在Rt△ABC中, , , , 将△ABC绕点C按逆时针方向旋转得到 , 此时点恰好在AB边上,则点与点B之间的距离为( )
A、1条 B、2条 C、3条 D、无数条6. 如图,在Rt△ABC中, , , , 将△ABC绕点C按逆时针方向旋转得到 , 此时点恰好在AB边上,则点与点B之间的距离为( ) A、10 B、20 C、 D、7. 如图,E是正方形ABCD中CD边上的点,以点A为中心,把△ADE顺时针旋转,得到△ABF.下列角中,是旋转角的是( )
A、10 B、20 C、 D、7. 如图,E是正方形ABCD中CD边上的点,以点A为中心,把△ADE顺时针旋转,得到△ABF.下列角中,是旋转角的是( ) A、∠DAE B、∠EAB C、∠DAB D、∠DAF8. 如图,平面内三点A、B、C,AB=4 , AC= , 以BC为对角线作正方形BDCE,连接AD,则AD的最大值是( )
A、∠DAE B、∠EAB C、∠DAB D、∠DAF8. 如图,平面内三点A、B、C,AB=4 , AC= , 以BC为对角线作正方形BDCE,连接AD,则AD的最大值是( ) A、5 B、 C、7 D、79. 如图,在中, , , BD是的角平分线,过点D作交BC边于点E.若 , 则图中阴影部分面积为 ( )
A、5 B、 C、7 D、79. 如图,在中, , , BD是的角平分线,过点D作交BC边于点E.若 , 则图中阴影部分面积为 ( ) A、2 B、4 C、3 D、510. 如图,在正方形网格中,绕某一点旋转某一角度得到 , 则旋转中心可能是( )
A、2 B、4 C、3 D、510. 如图,在正方形网格中,绕某一点旋转某一角度得到 , 则旋转中心可能是( ) A、点A B、点B C、点C D、点D
A、点A B、点B C、点C D、点D二、填空题(每题3分,共24分)
-
11. 如图,在中, , , 将绕点O逆时针转得到 , 则 .
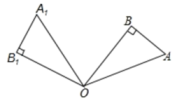 12. 如图,在中, , 在同一平面内,将绕点旋转到的位置,使得 , 则的度数为.
12. 如图,在中, , 在同一平面内,将绕点旋转到的位置,使得 , 则的度数为. 13. 如图,在平面直角坐标系中,每个小正方形边长均为1,将 ABC绕P点逆时针旋转至 ,使点B′恰好落在y轴上,则旋转中心P的坐标是.
13. 如图,在平面直角坐标系中,每个小正方形边长均为1,将 ABC绕P点逆时针旋转至 ,使点B′恰好落在y轴上,则旋转中心P的坐标是. 14. 如图,一个小孩坐在秋千上,秋千绕点O旋转了86°,小孩的位置也从A点运动到了点,则度.
14. 如图,一个小孩坐在秋千上,秋千绕点O旋转了86°,小孩的位置也从A点运动到了点,则度. 15. 如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A,D,E在同一条直线上,且AB=1,BC=2,则AD的值为.
15. 如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A,D,E在同一条直线上,且AB=1,BC=2,则AD的值为. 16. 如图,已知OD为等边△OAC的高,顶点 , , 若△OAC绕点O逆时针旋转,每秒旋转45°,则第60秒时,D点坐标为.
16. 如图,已知OD为等边△OAC的高,顶点 , , 若△OAC绕点O逆时针旋转,每秒旋转45°,则第60秒时,D点坐标为. 17. 旋转变换在几何证明或计算中有很重要的应用,利用旋转解决问题:如图,P为正方形 内一点, , , ,则 .
17. 旋转变换在几何证明或计算中有很重要的应用,利用旋转解决问题:如图,P为正方形 内一点, , , ,则 . 18. 如图,在△ABC中,AB=AC=4,∠C=30°,P在边BC上运动,连接AP,将线段AP绕点A顺时针旋转120°至AP′,则线段PP′的最小值为.
18. 如图,在△ABC中,AB=AC=4,∠C=30°,P在边BC上运动,连接AP,将线段AP绕点A顺时针旋转120°至AP′,则线段PP′的最小值为.
三、解答题(共7题,共66分)
-
19. 图中的图形均可以由“基本图案”通过变换得到.(填序号)
 (1)、通过平移变换但不能通过旋转变换得到的图案是;(2)、可以通过旋转变换但不能通过平移变换得到的图案是;(3)、既可以由平移变换,也可以由旋转变换得到的图案是.20. 如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长.
(1)、通过平移变换但不能通过旋转变换得到的图案是;(2)、可以通过旋转变换但不能通过平移变换得到的图案是;(3)、既可以由平移变换,也可以由旋转变换得到的图案是.20. 如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长. 21. 在如图所示的平面直角坐标系中,每个小正方形的边长均为1,的三个顶点均在格点上,且 , , (本题不必写作图结论).
21. 在如图所示的平面直角坐标系中,每个小正方形的边长均为1,的三个顶点均在格点上,且 , , (本题不必写作图结论).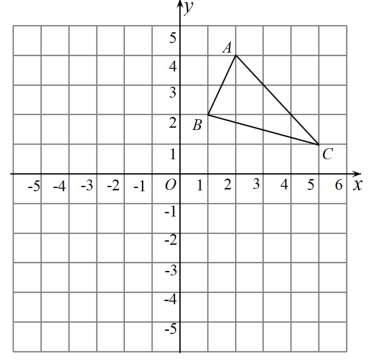
( 1 )将以点为旋转中心逆时针旋转 , 画出旋转后的 , 并直接写出点的坐标: ▲ , ▲ , ▲ ;
( 2 )画出向下平移6个单位长度后的 , 并直接写出点的坐标: ▲ , ▲ , ▲ ;
22. (1)、如图,在方格纸中如何通过平移或旋转这两种变换,由图形A 得到图形B.再由图形B先(怎样平移).再(怎样旋转)得到图形C(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度);(2)、如图,如果点P、P3的坐标分别为(0,0)、(2,1),写出点P2的坐标是;23. 如图,在平面直角坐标系中,的三个顶点分别是 , , .
(1)、如图,在方格纸中如何通过平移或旋转这两种变换,由图形A 得到图形B.再由图形B先(怎样平移).再(怎样旋转)得到图形C(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度);(2)、如图,如果点P、P3的坐标分别为(0,0)、(2,1),写出点P2的坐标是;23. 如图,在平面直角坐标系中,的三个顶点分别是 , , . (1)、将△ABC绕C点旋转180°,作出旋转后对应的△A1B1C1;(2)、平移△ABC到△A2B2C2 , 使点A的对应点A2的坐标为(﹣1,﹣4);(3)、若将△A1B1C1绕某一点旋转可以得到△A2B2C2 , 则该旋转中心的坐标为 .24. 如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F, .
(1)、将△ABC绕C点旋转180°,作出旋转后对应的△A1B1C1;(2)、平移△ABC到△A2B2C2 , 使点A的对应点A2的坐标为(﹣1,﹣4);(3)、若将△A1B1C1绕某一点旋转可以得到△A2B2C2 , 则该旋转中心的坐标为 .24. 如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F, .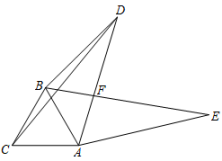 (1)、求的大小;(2)、连接DE,若BD=3,CD=5,求AD的长.25. 探索新知:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)、求的大小;(2)、连接DE,若BD=3,CD=5,求AD的长.25. 探索新知:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”. (1)、一个角的平分线这个角的“巧分线”;(填“是”或“不是”)(2)、如图2,若∠MPN=x,且射线PQ是∠MPN的“巧分线”,则∠MPQ=;(用含x的代数式表示出所有可能的结果)(3)、深入研究:如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.当t为何值时,射线PM是∠QPN的“巧分线”;
(1)、一个角的平分线这个角的“巧分线”;(填“是”或“不是”)(2)、如图2,若∠MPN=x,且射线PQ是∠MPN的“巧分线”,则∠MPQ=;(用含x的代数式表示出所有可能的结果)(3)、深入研究:如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.当t为何值时,射线PM是∠QPN的“巧分线”;