备战2023年中考数学细点逐一突破真题训练第9章二次函数图像性质
试卷更新日期:2023-03-08 类型:二轮复习
一、二次函数的概念性质
-
1. 下列各式中,y是x的二次函数的是( )A、 B、 C、 D、2. 关于二次函数 ,下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数有最大值,是大值是5 D、当 时,y随x的增大而增大3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 二次函数 的图象的对称轴是( )A、 B、 C、 D、5. 已知二次函数 ,当 时,y随x增大而增大,则实数a的取值范围是( )A、 B、 C、 D、6. 已知二次函数 , 设自变量的值分别为 , , , 且 , 则对应的函数值 , , 的大小关系是( )A、 B、 C、 D、7. 二次函数 的最大值是.8. 已知抛物线 上的部分点的横坐标x与纵坐标y的对应值如表:
x
…
-1
0
1
2
3
…
y
…
3
0
-1
m
3
…
以下结论正确的是( )
A、抛物线 的开口向下 B、当 时,y随x增大而增大 C、方程 的根为0和2 D、当 时,x的取值范围是9. 如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( ) A、1 B、2 C、3 D、410. 从 中任取一数作为 ,使抛物线 的开口向上的概率为 .11. 如图,对于抛物线y1=-x2+x+1, y2=-x2+2x+1, y3=-x2+3x+1,给出下列结论:①这三条抛物线都经过点C(0,1); ②抛物线y3的对称轴可由抛物线y1的对称轴向右平移1个单位而得到;③这三条抛物线的顶点在同一条直线上;④这三条抛物线与直线y=1的交点中,相邻两点之间的距离相等。其中正确结论的序号是。
A、1 B、2 C、3 D、410. 从 中任取一数作为 ,使抛物线 的开口向上的概率为 .11. 如图,对于抛物线y1=-x2+x+1, y2=-x2+2x+1, y3=-x2+3x+1,给出下列结论:①这三条抛物线都经过点C(0,1); ②抛物线y3的对称轴可由抛物线y1的对称轴向右平移1个单位而得到;③这三条抛物线的顶点在同一条直线上;④这三条抛物线与直线y=1的交点中,相邻两点之间的距离相等。其中正确结论的序号是。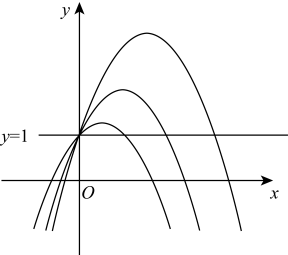 12. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .若抛物线 (h、k为常数)与线段 交于C、D两点,且 ,则k的值为 .
12. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .若抛物线 (h、k为常数)与线段 交于C、D两点,且 ,则k的值为 .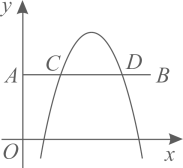
二、二次函数的平移规律
-
13. 把函数 的图象,经过怎样的平移变换以后,可以得到函数 的图象( )A、向左平移 个单位,再向下平移 个单位 B、向左平移 个单位,再向上平移 个单位 C、向右平移 个单位,再向上平移 个单位 D、向右平移 个单位,再向下平移 个单位14. 抛物线 可由抛物线 如何平移得到的( )A、先向左平移3个单位,再向下平移2个单位 B、先向左平移6个单位,再向上平移7个单位 C、先向上平移2个单位,再向左平移3个单位 D、先回右平移3个单位,再向上平移2个单位15. 如图,抛物线 经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积为.
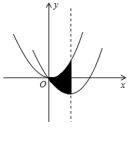
三、二次函数与系数a,b,c关系
-
16. 如图,二次函数y=ax2+bx+c(a为常数,且a≠0)的图象过点(﹣1,0),对称轴为直线x=1,且2<c<3,则下列结论正确的是( )
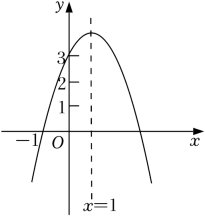 A、abc>0 B、3a+c>0 C、a2m2+abm≤a2+ab(m为任意实数) D、﹣1<a<﹣17. 已知二次函数的部分图象如图所示,对称轴为直线 , 有以下结论:①;②若t为任意实数,则有;③当图象经过点时,方程的两根为 , (),则 , 其中,正确结论的个数是( )
A、abc>0 B、3a+c>0 C、a2m2+abm≤a2+ab(m为任意实数) D、﹣1<a<﹣17. 已知二次函数的部分图象如图所示,对称轴为直线 , 有以下结论:①;②若t为任意实数,则有;③当图象经过点时,方程的两根为 , (),则 , 其中,正确结论的个数是( ) A、0 B、1 C、2 D、318. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,则有下列结论:① ;② ;③ ;④对于任意实数 , ;其中结论正确的个数为( )
A、0 B、1 C、2 D、318. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,则有下列结论:① ;② ;③ ;④对于任意实数 , ;其中结论正确的个数为( )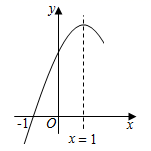 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个四、二次函数图像共存问题
-
19. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
 A、
A、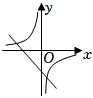 B、
B、 C、
C、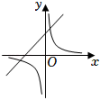 D、
D、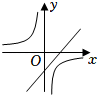 20. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )
20. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )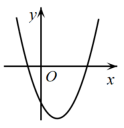 A、
A、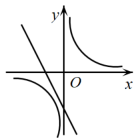 B、
B、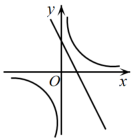 C、
C、 D、
D、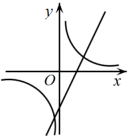 21. 已知一次函数的图像如图所示,则二次函数和反比例函数在同一坐标系内的图象可能是( )
21. 已知一次函数的图像如图所示,则二次函数和反比例函数在同一坐标系内的图象可能是( )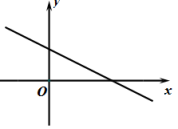 A、
A、 B、
B、 C、
C、 D、
D、 22. 如图,函数y=ax+a和y=ax2-2x+1(a是常数,且a≠0)在同一平面直角坐标系中的图象可能是( )A、
22. 如图,函数y=ax+a和y=ax2-2x+1(a是常数,且a≠0)在同一平面直角坐标系中的图象可能是( )A、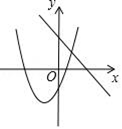 B、
B、 C、
C、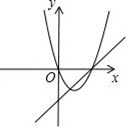 D、
D、
五、二次函数解析式确定
-
23. 二次函数y=ax2+bx+c的图象经过点A(4,0),B(0,﹣3),C(﹣2,0),求它的解析式,直接写出它的开口方向、对称轴和顶点坐标.24. 已知抛物线 经过点 和 .(1)、求 、 的值;(2)、将该抛物线向上平移2个单位长度,再向右平移1个单位长度,得到新的抛物线,直接写出新的抛物线相应的函数表达式.25. 如图,二次函数 (a为常数)的图象的对称轴为直线 .
 (1)、求a的值.(2)、向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.
(1)、求a的值.(2)、向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.六、二次函数与不等式,方程结合
-
26. 在平面直角坐标系中,已知二次函数y=-x2+2kx+k-1(k是常数).(1)、当k=-2时,求该二次函数图象与x轴的交点坐标;(2)、若该函数图象经过点(1,4),求该二次函数图象的顶点坐标;(3)、当0≤x≤1时,该函数有最大值4,求k的值.27. 已知二次函数 的图象如图所示,有下列结论:① ;② >0;③ ;④不等式 <0的解集为1≤x<3,正确的结论个数是( )
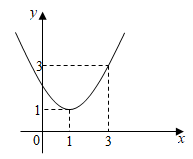 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4
