2022-2023学年初数北师大版八年级下册 3.1 图形的平移 同步必刷题
试卷更新日期:2023-03-08 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 在平面直角坐标系中将向左平移3个单位,则平移后的点的坐标是( )A、(7,5) B、(4,2) C、(1,5) D、(4,8)2. 在平面直角坐标系中,把点 向右平移3个单位长度,得到的点B的坐标为( )A、 B、 C、 D、3. 如图,沿直角边BC所在的直线向右平移得到 , 下列结论中错误的是( )
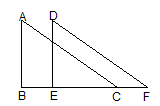 A、≌ B、 C、 D、4. 在平面直角坐标系内,将M(6,2)先向左平移4个单位,再向下平移2个单位,则移动后的点的坐标是 ( )A、(2,0) B、(10,4) C、(10,0) D、(2,4)5. 如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5cm,已知BC=3cm,AC=4cm,则阴影部分周长为( )
A、≌ B、 C、 D、4. 在平面直角坐标系内,将M(6,2)先向左平移4个单位,再向下平移2个单位,则移动后的点的坐标是 ( )A、(2,0) B、(10,4) C、(10,0) D、(2,4)5. 如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5cm,已知BC=3cm,AC=4cm,则阴影部分周长为( )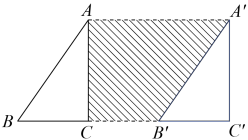 A、16cm B、18cm C、20cm D、22cm6. 第一象限内有两点P(m-4,n),Q(m,n-2),将线段PQ平移,使平移后的点P、Q分别在x轴与y轴上,则点P平移后的对应点的坐标是( )A、(-4,0) B、(4,0) C、(0,2) D、(0,-2)7. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=16,将△ABC沿CB方向向右平移得到△DEF,若四边形ABED的面积为24,则平移距离是( )
A、16cm B、18cm C、20cm D、22cm6. 第一象限内有两点P(m-4,n),Q(m,n-2),将线段PQ平移,使平移后的点P、Q分别在x轴与y轴上,则点P平移后的对应点的坐标是( )A、(-4,0) B、(4,0) C、(0,2) D、(0,-2)7. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=16,将△ABC沿CB方向向右平移得到△DEF,若四边形ABED的面积为24,则平移距离是( ) A、2 B、3 C、4 D、68. 如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)
A、2 B、3 C、4 D、68. 如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)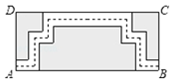 A、150米 B、125米 C、100米 D、75米9. 如图,是边长为2的等边三角形,将沿直线平移至的位置,连接 , 则的长是( )
A、150米 B、125米 C、100米 D、75米9. 如图,是边长为2的等边三角形,将沿直线平移至的位置,连接 , 则的长是( ) A、 B、2 C、 D、310. 如图,在平面直角坐标系中,点的坐标为 . 如果将轴向下平移4个单位,将轴向左平移1个单位,交于点 , 点的位置不变,那么在平面直角坐标系中,点的坐标是( )
A、 B、2 C、 D、310. 如图,在平面直角坐标系中,点的坐标为 . 如果将轴向下平移4个单位,将轴向左平移1个单位,交于点 , 点的位置不变,那么在平面直角坐标系中,点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共24分)
-
11. 如图,平移后得到 , 若 , , 则平移的距离的是 .
 12. 在平面直角坐标系中,点M(-4,1),先向右平移2个单位,再作关于y轴对称,最后得到的点的坐标为 .13. 把直线向上平移5个单位长度,平移后的直线与x轴的交点坐标为 .14. 已知点是由点A先向上平移4个单位,再向左平移3个单位得到的,则点A的坐标是 .15. 如图,已知一块直角三角板的直角顶点与原点O重合,另两个顶点A,B的坐标分别为 , , 现将该三角板向右平移使点A与点O重合,得到 , 则点B的对应点的坐标为.
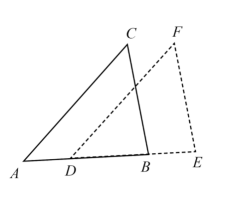
12. 在平面直角坐标系中,点M(-4,1),先向右平移2个单位,再作关于y轴对称,最后得到的点的坐标为 .13. 把直线向上平移5个单位长度,平移后的直线与x轴的交点坐标为 .14. 已知点是由点A先向上平移4个单位,再向左平移3个单位得到的,则点A的坐标是 .15. 如图,已知一块直角三角板的直角顶点与原点O重合,另两个顶点A,B的坐标分别为 , , 现将该三角板向右平移使点A与点O重合,得到 , 则点B的对应点的坐标为. 16. 已知△A'B'C'是由△ABC平移得到的(点A',B',C'分别是A、B、C的对应点),若点A的坐标为(﹣1,2),A'的坐标为(3,4),则点B(﹣3.﹣2)的对应点B'的坐标为 .17. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后得到△DEF,连接DC,则DC的长为.
16. 已知△A'B'C'是由△ABC平移得到的(点A',B',C'分别是A、B、C的对应点),若点A的坐标为(﹣1,2),A'的坐标为(3,4),则点B(﹣3.﹣2)的对应点B'的坐标为 .17. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后得到△DEF,连接DC,则DC的长为.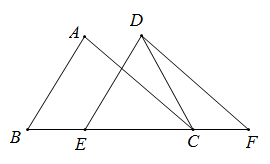 18. 学校会议室重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要元
18. 学校会议室重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要元
三、解答题(共7题,共66分)
-
19. 如图,在Rt中, , 将沿的方向平移得到 , 其中.
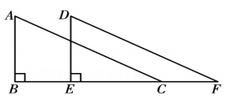 (1)、求的长;(2)、若 , 求的度数.20. 如图,平面直角坐标系中,三个顶点的坐标分别为 , , .
(1)、求的长;(2)、若 , 求的度数.20. 如图,平面直角坐标系中,三个顶点的坐标分别为 , , .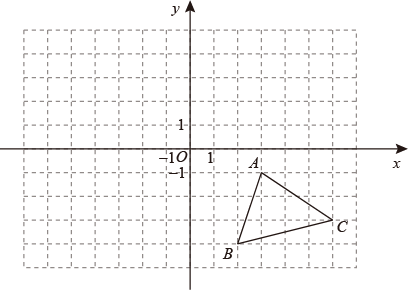
( 1 )请在图中画出与关于原点成中心对称的 , 并直接写出点 , , 的坐标: ▲ , ▲ , ▲ ;
( 2 )将点 , , 的横坐标分别加5,纵坐标分别减2,依次得到点 , , , 请在图中画出;
( 3 )若点是内的任意一点,点P经过(1)(2)中的两次变换后的对应点为 , 则点的坐标为 ▲ (用含m,n的式子表示).
21. 如图,已知△ABC在方格纸中,每个小正方形的边长为1个单位长度. (1)、△A1B1C1与△ABC关于x轴对称,请你在图中画出△A1B1C1;(2)、将△ABC向右平移4个单位后得到△A2B2C2 , 请你在图中画出△A2B2C2;并写出B2的坐标;(3)、在x轴上存在点M,使得MB+MC的值最小,请求出点M的坐标以及MB+MC的最小值.22. 如图,在直角坐标系中,已知点O,A的坐标分别为 , .
(1)、△A1B1C1与△ABC关于x轴对称,请你在图中画出△A1B1C1;(2)、将△ABC向右平移4个单位后得到△A2B2C2 , 请你在图中画出△A2B2C2;并写出B2的坐标;(3)、在x轴上存在点M,使得MB+MC的值最小,请求出点M的坐标以及MB+MC的最小值.22. 如图,在直角坐标系中,已知点O,A的坐标分别为 , . (1)、点B的坐标是 , 点B与点A之间的距离是 . 将点B,点A都向右平移5个单位长度分别得到对应点C和D,顺次连接点A,B,C,D,画出四边形;(2)、横、纵坐标都是整数的点称为整数点,在四边形内部(不包括边界)的整数点M使 , 请直接写出所有点M的可能坐标.23. 在平面直角坐标系xOy中,△ABC的顶点分别为A(1,1),B(2,4),C(4,2).
(1)、点B的坐标是 , 点B与点A之间的距离是 . 将点B,点A都向右平移5个单位长度分别得到对应点C和D,顺次连接点A,B,C,D,画出四边形;(2)、横、纵坐标都是整数的点称为整数点,在四边形内部(不包括边界)的整数点M使 , 请直接写出所有点M的可能坐标.23. 在平面直角坐标系xOy中,△ABC的顶点分别为A(1,1),B(2,4),C(4,2). (1)、画出△ABC关于原点O对称的△AB1C1;(2)、点 C关于x轴的对称点C2的坐标为;(3)、点C2向左平移m个单位后,落在△AB1C1内部,写出一个满足条件的m的值:.24. 如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2 , 点P2恰好在直线l上.
(1)、画出△ABC关于原点O对称的△AB1C1;(2)、点 C关于x轴的对称点C2的坐标为;(3)、点C2向左平移m个单位后,落在△AB1C1内部,写出一个满足条件的m的值:.24. 如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2 , 点P2恰好在直线l上. (1)、写出点P2的坐标;(2)、求直线l所表示的一次函数的表达式;(3)、若将点P2先向右平移3个单位,再向上平移6个单位得到像点P3 . 请判断点P3是否在直线l上,并说明理由.25. 在平面直角坐标系 中,对于点 ,如果点 满足条件:以线段 为对角线的正方形,且正方形的边分别与 轴, 轴平行,那么称点 为点 的“和谐点”,如下图所示.
(1)、写出点P2的坐标;(2)、求直线l所表示的一次函数的表达式;(3)、若将点P2先向右平移3个单位,再向上平移6个单位得到像点P3 . 请判断点P3是否在直线l上,并说明理由.25. 在平面直角坐标系 中,对于点 ,如果点 满足条件:以线段 为对角线的正方形,且正方形的边分别与 轴, 轴平行,那么称点 为点 的“和谐点”,如下图所示.已知点 , , .
 (1)、已知点 的坐标是 .
(1)、已知点 的坐标是 .①在 , , 中,是点 的“和谐点”的是 ▲ .
②已知点 的坐标为 ,如果点 为点 的“和谐点”,求 的值;
(2)、已知点 ,如果线段 上存在一个点 ,使得点 是点 的“和谐点”,直接写出 的取值范围.