安徽省、云南省、吉林省、黑龙江省2023届高三下学期数学2月适应性测试试卷
试卷更新日期:2023-03-08 类型:高考模拟
一、单选题
-
1. 设 , 则( )A、i B、 C、1 D、-12. 设集合 , , . 若 , , 则( )A、-3 B、-1 C、1 D、33. 甲、乙、丙、丁四名教师带领学生参加校园植树活动,教师随机分成三组,每组至少一人,则甲、乙在同一组的概率为( )A、 B、 C、 D、4. 平面向量与相互垂直,已知 , , 且与向量的夹角是钝角,则( )A、 B、 C、 D、5. 已知点A,B,C为椭圆D的三个顶点,若是正三角形,则D的离心率是( )A、 B、 C、 D、6. 三棱锥中,平面 , . 若 , , 则该三棱锥体积的最大值为( )A、2 B、 C、1 D、7. 设函数 , 在上的导函数存在,且 , 则当时( )A、 B、 C、 D、8. 已知a,b,c满足 , , 则( )A、 , B、 , C、 , D、 ,
二、多选题
-
9. 已知是定义在上的偶函数,是定义在上的奇函数,且 , 在单调递减,则( )A、 B、 C、 D、10. 已知平面平面 , B,D是l上两点,直线且 , 直线且 . 下列结论中,错误的有( )A、若 , , 且 , 则ABCD是平行四边形 B、若M是AB中点,N是CD中点,则 C、若 , , , 则CD在上的射影是BD D、直线AB,CD所成角的大小与二面角的大小相等11. 质点P和Q在以坐标原点O为圆心,半径为1的上逆时针作匀速圆周运动,同时出发.P的角速度大小为 , 起点为与x轴正半轴的交点;Q的角速度大小为 , 起点为射线与的交点.则当Q与P重合时,Q的坐标可以为( )A、 B、 C、 D、12. 下图改编自李约瑟所著的《中国科学技术史》,用于说明元代数学家郭守敬在编制《授时历》时所做的天文计算.图中的 , , , 都是以O为圆心的圆弧,CMNK是为计算所做的矩形,其中M,N,K分别在线段OD,OB,OA上, , . 记 , , , , 则( )
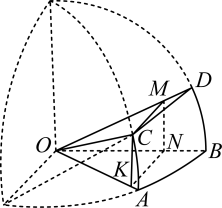 A、 B、 C、 D、
A、 B、 C、 D、三、填空题
-
13. 某工厂生产的产品的质量指标服从正态分布 . 质量指标介于99至101之间的产品为良品,为使这种产品的良品率达到 , 则需调整生产工艺,使得至多为 . (若 , 则)14. 若P,Q分别是抛物线与圆上的点,则的最小值为 .15. 数学家祖冲之曾给出圆周率的两个近似值:“约率”与“密率” . 它们可用“调日法”得到:称小于3.1415926的近似值为弱率,大于3.1415927的近似值为强率.由 , 取3为弱率,4为强率,得 , 故为强率,与上一次的弱率3计算得 , 故为强率,继续计算,…….若某次得到的近似值为强率,与上一次的弱率继续计算得到新的近似值;若某次得到的近似值为弱率,与上一次的强率继续计算得到新的近似值,依此类推,已知 , 则; .16. 图为一个开关阵列,每个开关只有“开”和“关”两种状态,按其中一个开关1次,将导致自身和所有相邻的开关改变状态.例如,按将导致 , , , , 改变状态.如果要求只改变的状态,则需按开关的最少次数为 .
四、解答题
-
17. 如图,四边形ABCD是圆柱底面的内接四边形,是圆柱的底面直径,是圆柱的母线,E是AC与BD的交点, , .
 (1)、记圆柱的体积为 , 四棱锥的体积为 , 求;(2)、设点F在线段AP上, , 求二面角的余弦值.18. 已知函数在区间单调,其中为正整数, , 且 .(1)、求图像的一条对称轴;(2)、若 , 求 .19. 记数列的前n项和为 , 且 .(1)、求数列的通项公式;(2)、设m为整数,且对任意 , , 求m的最小值.20. 一个池塘里的鱼的数目记为N,从池塘里捞出200尾鱼,并给鱼作上标识,然后把鱼放回池塘里,过一小段时间后再从池塘里捞出500尾鱼,表示捞出的500尾鱼中有标识的鱼的数目.(1)、若 , 求的数学期望;(2)、已知捞出的500尾鱼中15尾有标识,试给出N的估计值(以使得最大的N的值作为N的估计值).21. 已知双曲线过点 , 且焦距为10.(1)、求C的方程;(2)、已知点 , E为线段AB上一点,且直线DE交C于G,H两点.证明: .22. 椭圆曲线加密算法运用于区块链.
(1)、记圆柱的体积为 , 四棱锥的体积为 , 求;(2)、设点F在线段AP上, , 求二面角的余弦值.18. 已知函数在区间单调,其中为正整数, , 且 .(1)、求图像的一条对称轴;(2)、若 , 求 .19. 记数列的前n项和为 , 且 .(1)、求数列的通项公式;(2)、设m为整数,且对任意 , , 求m的最小值.20. 一个池塘里的鱼的数目记为N,从池塘里捞出200尾鱼,并给鱼作上标识,然后把鱼放回池塘里,过一小段时间后再从池塘里捞出500尾鱼,表示捞出的500尾鱼中有标识的鱼的数目.(1)、若 , 求的数学期望;(2)、已知捞出的500尾鱼中15尾有标识,试给出N的估计值(以使得最大的N的值作为N的估计值).21. 已知双曲线过点 , 且焦距为10.(1)、求C的方程;(2)、已知点 , E为线段AB上一点,且直线DE交C于G,H两点.证明: .22. 椭圆曲线加密算法运用于区块链.椭圆曲线 . 关于x轴的对称点记为 . C在点处的切线是指曲线在点P处的切线.定义“”运算满足:①若 , 且直线PQ与C有第三个交点R,则;②若 , 且PQ为C的切线,切点为P,则;③若 , 规定 , 且 .
参考公式:
(1)、当时,讨论函数零点的个数;(2)、已知“”运算满足交换律、结合律,若 , 且PQ为C的切线,切点为P,证明:;(3)、已知 , 且直线PQ与C有第三个交点,求的坐标.