浙江省嵊州市2022-2023学年九年级上学期期末考试数学试题
试卷更新日期:2023-03-08 类型:期末考试
一、单选题
-
1. 已知 , 是锐角,则的度数为( )A、 B、 C、 D、2. 若 , 则的值为( )A、 B、 C、 D、3. 如图,在中, , 点是优弧上一点,则的度数为( )
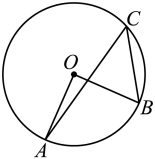 A、 B、 C、 D、4. 在一个暗箱里放有个除颜色外完全相同的球,这个球中红球只有4个,每次将球充分摇匀后,随机从中摸出一球,记下颜色后放回,通过大量的重复试验后发现,摸到红球的频率为0.4,由此可以推算出约为( )A、7 B、3 C、10 D、65. 二次函数均为常数的图象经过 , , 三点,则 , , 的大小关系是( )A、 B、 C、 D、6. 如图,在由小正方形组成的方格纸中,和的顶点均在格点上,要使 , 则点所在的格点为( )
A、 B、 C、 D、4. 在一个暗箱里放有个除颜色外完全相同的球,这个球中红球只有4个,每次将球充分摇匀后,随机从中摸出一球,记下颜色后放回,通过大量的重复试验后发现,摸到红球的频率为0.4,由此可以推算出约为( )A、7 B、3 C、10 D、65. 二次函数均为常数的图象经过 , , 三点,则 , , 的大小关系是( )A、 B、 C、 D、6. 如图,在由小正方形组成的方格纸中,和的顶点均在格点上,要使 , 则点所在的格点为( )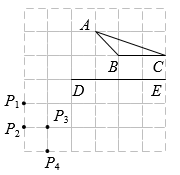 A、 B、 C、 D、7. 在学习画线段的黄金分割点时,小明过点B作的垂线 , 取的中点M,以点B为圆心,为半径画弧交射线于点D,连接 , 再以点D为圆心,为半径画弧,前后所画的两弧分别与交于E,F两点,最后,以A为圆心,“■■”的长度为半径画弧交于点H,点H即为的其中一个黄金分割点,这里的“■■”指的是线段( )
A、 B、 C、 D、7. 在学习画线段的黄金分割点时,小明过点B作的垂线 , 取的中点M,以点B为圆心,为半径画弧交射线于点D,连接 , 再以点D为圆心,为半径画弧,前后所画的两弧分别与交于E,F两点,最后,以A为圆心,“■■”的长度为半径画弧交于点H,点H即为的其中一个黄金分割点,这里的“■■”指的是线段( ) A、 B、 C、 D、8. 如图,在中, , 若 , , 点是上一点,且 , 则的值为( ).
A、 B、 C、 D、8. 如图,在中, , 若 , , 点是上一点,且 , 则的值为( ).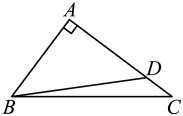 A、 B、 C、 D、9. 如图,在半径为5的中,是直径,是弦,是的中点,与交于点.若 , 则的长为( )
A、 B、 C、 D、9. 如图,在半径为5的中,是直径,是弦,是的中点,与交于点.若 , 则的长为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,与轴交于A,B两点(在的左侧),与轴交于点 , 点是上方抛物线上一点,连结交于点 , 连结AC,CP,记的面积为 , 的面积为 , 则的最小值为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,与轴交于A,B两点(在的左侧),与轴交于点 , 点是上方抛物线上一点,连结交于点 , 连结AC,CP,记的面积为 , 的面积为 , 则的最小值为( ) A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题
-
11. 图中的两个三角形是否相似,(填“是”或“否”).
 12. 如图是刚刚结束的2022年第22届卡塔尔世界杯发行的官方纪念币,它们分别是①世界杯会徽,②世界杯口号,③大力神杯,④吉祥物,⑤多哈塔尔塔,⑥阿尔拜特体育场,⑦卡塔尔地图,⑧卢赛尔体育场.现有8张形状、大小、质地均相同的卡片,正面分别印有世界杯会徽,世界杯口号,大力神杯,吉祥物,多哈塔尔塔,阿尔拜特体育场,卡塔尔地图,卢赛尔体育场种不同的图案,背面完全相同.现将这8张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是世界杯会徽图案的概率是.
12. 如图是刚刚结束的2022年第22届卡塔尔世界杯发行的官方纪念币,它们分别是①世界杯会徽,②世界杯口号,③大力神杯,④吉祥物,⑤多哈塔尔塔,⑥阿尔拜特体育场,⑦卡塔尔地图,⑧卢赛尔体育场.现有8张形状、大小、质地均相同的卡片,正面分别印有世界杯会徽,世界杯口号,大力神杯,吉祥物,多哈塔尔塔,阿尔拜特体育场,卡塔尔地图,卢赛尔体育场种不同的图案,背面完全相同.现将这8张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是世界杯会徽图案的概率是. 13. 如图,在由相同的菱形组成的网格中, , 小菱形的顶点称为格点,已知点A,B,C,D,E都在格点上,连接 , , 的值为.
13. 如图,在由相同的菱形组成的网格中, , 小菱形的顶点称为格点,已知点A,B,C,D,E都在格点上,连接 , , 的值为. 14. 如图,是的直径,弦与相交于点 , 若 , , , 则到的距离为.
14. 如图,是的直径,弦与相交于点 , 若 , , , 则到的距离为. 15. 二次函数的图象上任意二点连线不与轴平行,则的取值范围为.16. 如图,矩形中, , , 是射线上一动点,连结交对角线于点 , 当把分成一个三角形和一个四边形时,这个三角形的面积恰好是面积的 , 则的长为.
15. 二次函数的图象上任意二点连线不与轴平行,则的取值范围为.16. 如图,矩形中, , , 是射线上一动点,连结交对角线于点 , 当把分成一个三角形和一个四边形时,这个三角形的面积恰好是面积的 , 则的长为.
三、解答题
-
17.(1)、计算:.(2)、已知线段c是线段a,b的比例中项,若 , , 求线段c的长.18. 在的方格纸中,点A,B,C,D,E,F分别位于如图所示的小正方形的顶点上.
 (1)、从C,D,E,F四点中任意取一点,以所取的这一点及A,B为顶点画三角形,则所画三角形是等腰三角形的概率是.(2)、从C,D,E,F四点中任意取两个不同的点,以所取的这两点及A,B为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表求解).19. 如图1是嵊州市某小区的“垃圾分类定时定点投放点”,智能化按键式开启投放门的投放方式,让嵊州人民的垃圾投放变得更智能更环保,图2是投放门开启后的侧面示意图,投放口挡板长45cm,挡板底部距地面高为125cm,挡板开启后的最大张角为 , 求投放门前端C离开的最大距离及投放门前端C距地面的最大距离(参考数据: , , , 结果精确到1cm)
(1)、从C,D,E,F四点中任意取一点,以所取的这一点及A,B为顶点画三角形,则所画三角形是等腰三角形的概率是.(2)、从C,D,E,F四点中任意取两个不同的点,以所取的这两点及A,B为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表求解).19. 如图1是嵊州市某小区的“垃圾分类定时定点投放点”,智能化按键式开启投放门的投放方式,让嵊州人民的垃圾投放变得更智能更环保,图2是投放门开启后的侧面示意图,投放口挡板长45cm,挡板底部距地面高为125cm,挡板开启后的最大张角为 , 求投放门前端C离开的最大距离及投放门前端C距地面的最大距离(参考数据: , , , 结果精确到1cm)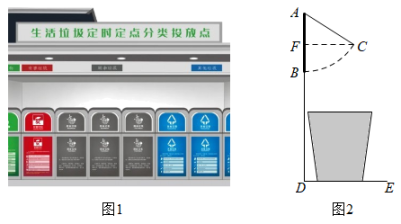 20. 如图,四边形内接于 , 分别延长 , , 使它们相交于点 , , 且.
20. 如图,四边形内接于 , 分别延长 , , 使它们相交于点 , , 且.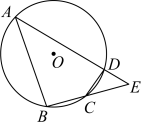 (1)、求证:.(2)、若 , 点为的中点,求的半径.21. 在卡塔尔世界杯期间,图1是某足球运动员在比赛期间的进球瞬间,足球在抽射过程中恰好碰到防守队员的身体,改变足球线路,弹射入网.小冲在训练过程中也尝试这样的射门,如图2是小冲在训练时的示意图,足球在空中的运动轨迹可以抽象成一条抛物线,假设足球在碰到障碍平台后的运动轨迹,与末碰到障碍平台前的轨迹的形状完全相同,且达到最高点时离地高度也相同 , 并且两条轨迹在同一平面内,射门时的起脚点与障碍平台之间的距离为 , 障碍平台高为 , 若小冲此次训练时足球正好在前方的点处达到最高点,离地面最高距离为 , 以地面所在直线为轴,过点且垂直于的直线为轴建立平面直角坐标系.
(1)、求证:.(2)、若 , 点为的中点,求的半径.21. 在卡塔尔世界杯期间,图1是某足球运动员在比赛期间的进球瞬间,足球在抽射过程中恰好碰到防守队员的身体,改变足球线路,弹射入网.小冲在训练过程中也尝试这样的射门,如图2是小冲在训练时的示意图,足球在空中的运动轨迹可以抽象成一条抛物线,假设足球在碰到障碍平台后的运动轨迹,与末碰到障碍平台前的轨迹的形状完全相同,且达到最高点时离地高度也相同 , 并且两条轨迹在同一平面内,射门时的起脚点与障碍平台之间的距离为 , 障碍平台高为 , 若小冲此次训练时足球正好在前方的点处达到最高点,离地面最高距离为 , 以地面所在直线为轴,过点且垂直于的直线为轴建立平面直角坐标系.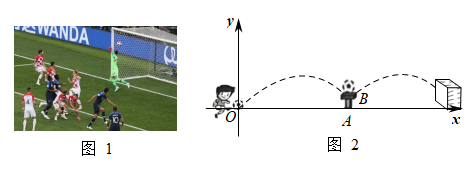 (1)、求过O,C,B三点的抛物线表达式;(2)、此时障碍平台与球门之间的距离为 , 已知球门高为 , 请你通过计算,(不考虑其他因素)足球在经过障碍平台的反弹后能否顺利射入球门.22. 为了充分利用四边形余料,小明设计了不同的方案裁剪正方形,裁剪方案与数据如下表:
(1)、求过O,C,B三点的抛物线表达式;(2)、此时障碍平台与球门之间的距离为 , 已知球门高为 , 请你通过计算,(不考虑其他因素)足球在经过障碍平台的反弹后能否顺利射入球门.22. 为了充分利用四边形余料,小明设计了不同的方案裁剪正方形,裁剪方案与数据如下表:方案设计
方案1
方案2
裁剪方案示意图


说明
图中的正方形和正方形四个顶点都在原四边形的边上
测量数据
, , , ;
任务1:探寻边角
填空: ▲ , ▲ ;
任务2:比较面积
计算或推理:正方形和正方形边长之比;
任务3:应用实践
若在余料上再截取一个最大正方形,正方形的边长为 ▲ .
