浙江省宁波市镇海区2022-2023学年七年级上学期期末数学试题
试卷更新日期:2023-03-08 类型:期末考试
一、单选题
-
1. 的相反数是( )A、-2 B、2 C、 D、2. 在党的二十大报告中总结了新时代十年的非凡成就,包括我国建成世界上规模最大的社会保障体系,基本养老保险覆盖10.4亿人,其中10.4亿用科学记数法可表示为( )A、 B、 C、 D、3. 下列各数: , , , , , 0, , 2.101101110…(每两个0之同次多一个1),其中是无理数的个数是( )A、3个 B、4个 C、5个 D、6个4. 下列说法正确的是( )A、是多项式 B、是单项式 C、是五次单项式 D、是四次多项式5. 已知 , 则的值为( )A、10 B、不能确定 C、-6 D、-106. 下列对方程进行的变形中,正确的是( )A、4x-5=3x+2变形得4x-3x=-2+5 B、x-1=x+3变形得4x-6=3x+18 C、3(x-1)=2(x+3)变形得3x-1-2x+6 D、3x=2变形得x=7. 如图,直线相交于点O, , 若 , 则的度数为( )
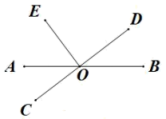 A、 B、 C、 D、8. 我国古代数学著作《孙子算经》卷中记载“多人共车”问题,原文如下:“今有三人共车,二车空;二人共车,九人步,问人与车各几何?”意思是:今有若干人乘车,每3人乘1车,最终剩余2辆车;若每2人共乘1车,最终剩余9个人无车可乘,问有多少人,多少辆车?设有x个人,根据题意列方程正确的是( )A、 B、 C、 D、9. 数轴上,有理数a、b、-a、c的位置如图,则化简的结果为( )
A、 B、 C、 D、8. 我国古代数学著作《孙子算经》卷中记载“多人共车”问题,原文如下:“今有三人共车,二车空;二人共车,九人步,问人与车各几何?”意思是:今有若干人乘车,每3人乘1车,最终剩余2辆车;若每2人共乘1车,最终剩余9个人无车可乘,问有多少人,多少辆车?设有x个人,根据题意列方程正确的是( )A、 B、 C、 D、9. 数轴上,有理数a、b、-a、c的位置如图,则化简的结果为( )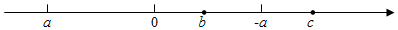 A、 B、 C、 D、010. 在长方形中将正方形、正方形、长方形和长方形按如图所示位置摆放,若已知两阴影部分周长之差,则一定能求出( )
A、 B、 C、 D、010. 在长方形中将正方形、正方形、长方形和长方形按如图所示位置摆放,若已知两阴影部分周长之差,则一定能求出( ) A、正方形的周长 B、正方形的周长 C、长方形中的长度 D、长方形中的长度
A、正方形的周长 B、正方形的周长 C、长方形中的长度 D、长方形中的长度二、填空题
-
11. 请写出一个大于-4而小于-3的无理数 .
12. 已知 , 则的补角的度数为.13. 若的值为5,则的值为.14. 如图,点B在线段上,已知 , , 点O是线段的中点,则线段cm.
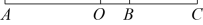 15. 多项式 与另一个多项式的和为 ,该多项式应为.16. 已知关于x的方程与的解相同,则.17. 钟表上显示为3时40分,则时针与分针的夹角大小为度.18. 将相同的长方形卡片按如图方式摆放在一个直角上,每个长方形卡片长为2,宽为1,依此类推,摆放2023个时,实线部分长为.
15. 多项式 与另一个多项式的和为 ,该多项式应为.16. 已知关于x的方程与的解相同,则.17. 钟表上显示为3时40分,则时针与分针的夹角大小为度.18. 将相同的长方形卡片按如图方式摆放在一个直角上,每个长方形卡片长为2,宽为1,依此类推,摆放2023个时,实线部分长为.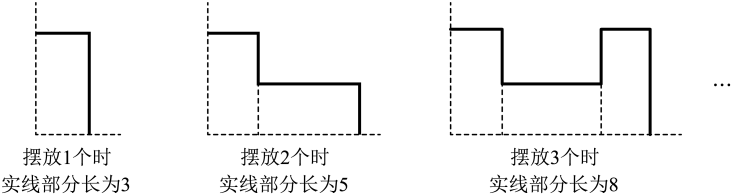
三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、(2)、21. 先化简,再求值: , 其中 , .22. 如图,已知三个点A、B、C,按下列要求画图.
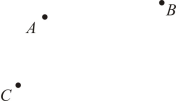
⑴画直线;
⑵画射线;
⑶过B点画直线的垂线段,垂足为F.(画图工具不限,不需写出结论,只需画出图形、标注字母)
23. 如图,点O为数轴原点,点A对应的数为-5,点B对应的数为10. (1)、点C是数轴上A、B之间的一个点,且 , 求线段CA的长及点C对应的数.(2)、点P从点A出发以每秒2个单位的速度沿数轴正方向运动,点Q从点B出发以每秒1个单位的速度沿数轴负方向运动.P、Q两点同时出发,设运动时间为t秒.当满足 , 求运动时间t.24. 一种商品按销售量分三部分制定销售单价,如下表:
(1)、点C是数轴上A、B之间的一个点,且 , 求线段CA的长及点C对应的数.(2)、点P从点A出发以每秒2个单位的速度沿数轴正方向运动,点Q从点B出发以每秒1个单位的速度沿数轴负方向运动.P、Q两点同时出发,设运动时间为t秒.当满足 , 求运动时间t.24. 一种商品按销售量分三部分制定销售单价,如下表:销售量
单价
不超过100件部分
2.6元/件
超过100件不超过300件部分
2.2元/件
超过300件部分
2元/件
(1)、若买100件花元,买300件花元;买380件花元;(2)、小明买这种商品花了568元,列方程求购买这种商品多少件?(3)、若小明花了n元(n>260),恰好购买0.45n件这种商品,求n的值.25. 如图1,已知点O在直线AB上,射线OD、OC分别在直线AB的上、下两侧且 , OE始终是的平分线. (1)、若 , 求的度数.(2)、如图2,设 , 已知 , 求n的值.(3)、如图3,在满足(2)的条件下,射线OP从OB出发绕点O以每秒的速度逆时针旋转,射线OQ从OE出发绕点O以每秒的速度顺时针旋转,射线OP、OQ同时开始旋转,记旋转时间为t秒.当和互余时,求旋转时间t的值.
(1)、若 , 求的度数.(2)、如图2,设 , 已知 , 求n的值.(3)、如图3,在满足(2)的条件下,射线OP从OB出发绕点O以每秒的速度逆时针旋转,射线OQ从OE出发绕点O以每秒的速度顺时针旋转,射线OP、OQ同时开始旋转,记旋转时间为t秒.当和互余时,求旋转时间t的值.