浙江省宁波市江北区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-03-08 类型:期末考试
一、单选题
-
1. 若 , 则的值为( )A、 B、 C、 D、2. 下列事件是必然事件的是( )A、足球运动员在罚球区射门一次,射中 B、从煮熟的鸡蛋里孵出小鸡,神奇 C、将实心铅球投入水中,下沉 D、雨后见彩虹,幸运3. 如图所示, , , , 则的长为( )
 A、 B、2 C、3 D、44. 如图,在中, , , , 则( )
A、 B、2 C、3 D、44. 如图,在中, , , , 则( )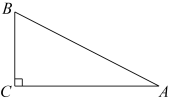 A、 B、 C、4 D、5. 关于二次函数 , 下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数的最大值是5 D、当时,y随x的增大而增大6. 如图,在中, , 若 , 则的度数为( )
A、 B、 C、4 D、5. 关于二次函数 , 下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数的最大值是5 D、当时,y随x的增大而增大6. 如图,在中, , 若 , 则的度数为( ) A、 B、 C、 D、7. 如图,点P为外一点,连结 , 作以为直径的圆,两圆交于点Q,连接 , 可得是的切线,则判定其为切线的依据是( )
A、 B、 C、 D、7. 如图,点P为外一点,连结 , 作以为直径的圆,两圆交于点Q,连接 , 可得是的切线,则判定其为切线的依据是( ) A、经过半径的外端并且垂直这条半径的直线是圆的切线 B、垂线段最短 C、过直线外一点,有且只有一条直线与已知直线垂直 D、过圆外一点所作的圆的两条切线长相等8. 如图,点G是的重心,于点H,若 , , 则△ABC的面积为( )
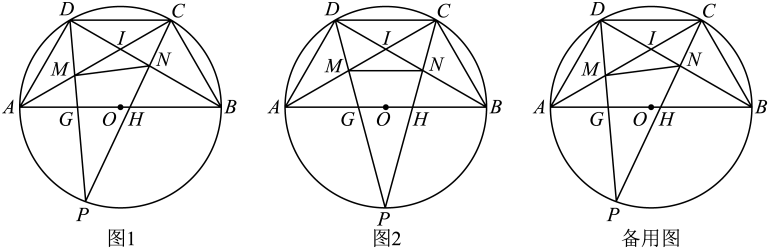
A、经过半径的外端并且垂直这条半径的直线是圆的切线 B、垂线段最短 C、过直线外一点,有且只有一条直线与已知直线垂直 D、过圆外一点所作的圆的两条切线长相等8. 如图,点G是的重心,于点H,若 , , 则△ABC的面积为( ) A、2 B、3 C、4 D、69. 定义:在 , D,E分别是两边的中点,如果上的所有点都在的内部或边上,则称为的中内弧.如图1,是的一条中内弧,如图2,在中, , D,E分别是AB,AC的中点.则所有中内弧所组成的图形(图中阴影部分表示)为( )
A、2 B、3 C、4 D、69. 定义:在 , D,E分别是两边的中点,如果上的所有点都在的内部或边上,则称为的中内弧.如图1,是的一条中内弧,如图2,在中, , D,E分别是AB,AC的中点.则所有中内弧所组成的图形(图中阴影部分表示)为( ) A、
A、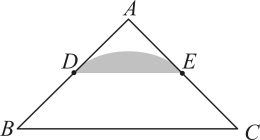 B、
B、 C、
C、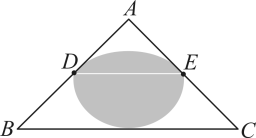 D、
D、 10. 已知二次函数 , 当时,y有最小值和最大值5,则m的取值范围为( )A、 B、 C、 D、
10. 已知二次函数 , 当时,y有最小值和最大值5,则m的取值范围为( )A、 B、 C、 D、二、填空题
-
11. 请写出一个主视图、左视图和俯视图完全一样的几何体 .12. 淘宝某商户为了解新商品主图是否吸引人,对该商品的点击量和展现量进行了监测,得到商品点击率如下表所示:(注:)
展现量
50
100
1000
5000
10000
50000
100000
点击量
4
7
78
385
760
3800
7600
点击率
根据上表,估计该商品展现量为30000时,点击率约为.
13. 如图,圆锥的侧面展开图是一个扇形,若圆锥的底面圆的半径 , 母线长 , 则侧面展开图的圆心角的度数为.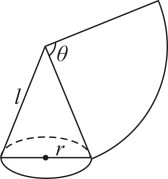 14. 刘徽是我国魏晋时期卓越的数学家,他首次提出“割圆术”,利用圆内接正多边形逐步逼近圆来近似计算圆周率,方法如图:作正六边形ABCDEF内接于 , 取的中点G,与交于点H;连接、;依次对剩余五段弧取中点可得一个圆内接正十二边形,记正十二边形的面积为 , 正六边形的面积为 , 则.
14. 刘徽是我国魏晋时期卓越的数学家,他首次提出“割圆术”,利用圆内接正多边形逐步逼近圆来近似计算圆周率,方法如图:作正六边形ABCDEF内接于 , 取的中点G,与交于点H;连接、;依次对剩余五段弧取中点可得一个圆内接正十二边形,记正十二边形的面积为 , 正六边形的面积为 , 则. 15. 有一个开口向下的二次函数,下表是函数中四对x与y的对应值.
15. 有一个开口向下的二次函数,下表是函数中四对x与y的对应值.x
…
0
1
2
…
y
…
…
若其中有一对对应值有误,则对于该二次函数,当时,x的取值范围是.
16. 如图,是半圆的直径且.P为半圆上一点(不与点A、B重合),D为延长线上一点,、的角平分线相交于点C.在点P移动的过程中,线段扫过的面积为.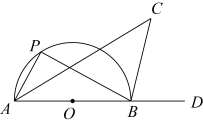
三、解答题
-
17.(1)、计算:.(2)、求二次函数的图象与x轴的交点坐标.18. 甲、乙、丙三名同学玩石头剪刀布游戏,规则如下:若其中两人出的手势相同,另一人不同,则按以下方式分胜负:石头赢剪刀、剪刀赢布、布赢石头;其他情况则为平局.(1)、甲同学决定随机出一个手势,则他出的手势为剪刀的概率为.(2)、若甲同学出的是剪刀,请用画树状图或列表的方法,求甲同学获胜的概率.19. 如图,在的正方形网格中,每个小正方形的顶点叫做格点,经过格点 , 仅用无刻度的直尺在给定网格中画图.(保留作图痕迹)
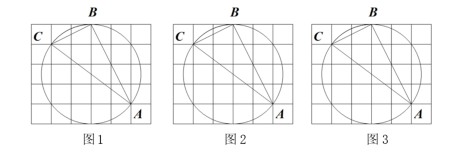 (1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.20. 图1,图2分别是某超市购物车的实物图与示意图,小江获得了如下信息: , , , , , , , .请根据以上信息,解决下列问题.(结果精确到 , 参考数据: , , )
(1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.20. 图1,图2分别是某超市购物车的实物图与示意图,小江获得了如下信息: , , , , , , , .请根据以上信息,解决下列问题.(结果精确到 , 参考数据: , , ) (1)、求点D到所在直线的距离.(2)、求的长度.21. 如图,为半圆O的直径,C为半圆上一点,连接 , 点D为的中点,过D作 , 交的延长线于点E.
(1)、求点D到所在直线的距离.(2)、求的长度.21. 如图,为半圆O的直径,C为半圆上一点,连接 , 点D为的中点,过D作 , 交的延长线于点E.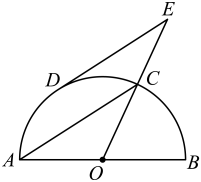 (1)、求证:是半圆O的切线.(2)、若 , , 求的长.22. 用长为8米的铝合金条制成如图窗框,已知矩形 , 矩形 , 矩形的面积均相等,设的长为米.
(1)、求证:是半圆O的切线.(2)、若 , , 求的长.22. 用长为8米的铝合金条制成如图窗框,已知矩形 , 矩形 , 矩形的面积均相等,设的长为米.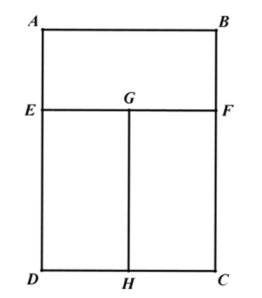 (1)、请用含的代数式表示的长.(2)、设矩形的面积为 , 出于实际考虑,我们要求窗框的高度()至少为1米,宽度()至少为1.5米,则当取何值时,透光面积最大,并求出面积的最大值.
(1)、请用含的代数式表示的长.(2)、设矩形的面积为 , 出于实际考虑,我们要求窗框的高度()至少为1米,宽度()至少为1.5米,则当取何值时,透光面积最大,并求出面积的最大值.