浙江省宁波市海曙区2022-2023学年七年级上学期期末数学试题

试卷更新日期：2023-03-08 类型：期末考试

进入出卷网下载

一、单选题

1. 2022的相反数是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 宁波文创港三期已正式开工建设，总建筑面积约 $272000 m^{2}$ ， 272000用科学记数法表示，正确的是（）

A、 $27.2 \times 1 0^{4}$ B、 $2.72 \times 1 0^{5}$ C、 $2.72 \times 1 0^{4}$ D、 $0.272 \times 1 0^{6}$

查看试题解析
3. 下列各式计算结果为负数的是（）

A、 $- 3 + 2$ B、 $2 - (- 3)$ C、 $3 \times 2$ D、 $(- 3) \div (- 2)$

查看试题解析
4. $M$ 、 $N$ 、 $P$ 、 $Q$ 四个点在数轴上的位置如图所示，则这四个点表示的四个数中绝对值最大的是（）

A、 $M$ B、 $N$ C、 $P$ D、 $Q$

查看试题解析
5. 下列说法错误是（）

A、数字2是单项式 B、单项式x的系数是1 C、 $x^{3} + x$ 是三次二项式 D、 $a^{2} b$ 与 $a b^{2}$ 是同类项

查看试题解析
6. 把弯曲的道路改直就能缩短路程，下列数学语言解释正确的是（）

A、垂线段最短 B、两点确定一条直线 C、两点之间线段最短 D、对顶角相等

查看试题解析
7. 根据等式的性质，下列变形不成立的是（）

A、若 $a = b$ ，则 $2 a = 2 b$ B、若 $a = b$ ，则 $\frac{a}{3} = \frac{b}{3}$ C、若 $a = b$ ，则 $2 - \frac{a}{3} = 2 - \frac{b}{3}$ D、若 $a = b$ ，则 $a + 1 = b - 1$

查看试题解析
8. 下列说法正确的是（）

A、4的平方根是2 B、8的立方根是±2 C、如果一个数的立方根是这个数本身，那么这个数是-1，0或1 D、如果一个数的平方根是这个数本身，那么这个数是1或0

查看试题解析
9. 如图，各网格中四个数之间都有相同的规律，则第7个网格中右下角的数为（）

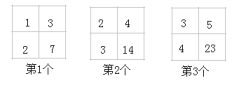A、62 B、79 C、88 D、98

查看试题解析
10. 已知关于x的一元一次方程 $\frac{x}{2023} + a = 2023 x$ 的解是 $x = 2022$ ，关于y的一元一次方程 $\frac{b}{2023} + 2023 c = - a$ 的解是 $y = - 2021$ （其中b和c是含有y的代数式），则下列结论符合条件的是（）

A、 $b = - y - 1 ， c = y + 1$ B、 $b = 1 - y ， c = y - 1$ C、 $b = y + 1 ， c = - y - 1$ D、 $b = y - 1 ， c = 1 - y$

查看试题解析

二、填空题

11. 甲、乙两地的海拔高度分别为20m和 $- 10 m$ ，则甲地比乙地高 $m ．$

查看试题解析
12. 下列各数： $\frac{1}{3} ， \sqrt{8} ， 2 π ， \sqrt[3]{8}$ 中，无理数有个.

查看试题解析
13. 比较大小： $\sqrt{11}$ $\sqrt[3]{27}$ （填＞、＜或＝）.

查看试题解析
14. 若 $2 x^{3} y^{m} 与 - 3 x^{n} y^{2}$ 是同类项，则 $m + n =$ ．

查看试题解析

三、解答题

15. 如图，在3×3的正方形网格中，请画出一个以格点为顶点，面积是5的正方形.

查看试题解析

四、填空题

16. 一个角比它的余角大 $20 °$ ，则这个角的补角度数是.

查看试题解析
17. 已知线段AB=12，C是线段AB上一点，且BC=2，点D在射线AB上，若DA=4DC，则BD的长为.

查看试题解析
18. 如图1，将一块长方形纸板四角各切去一个同样的正方形，制成图2的无盖纸盒.下列给出的条件中，能求得纸盒底面周长的有.（填序号）
①图1中，原长方形的周长和切去的正方形面积；
②图1中，原长方形的面积和切去的正方形面积；
③图1中切去的正方形面积和图2中长方体的侧面积；
④图1中原长方形边上的四个长方形中任何一个的长，宽和图2中长方体的体积.

查看试题解析

五、解答题

19. 计算：

(1)、 $3 - (- 8) + (- 5)$ ；

(2)、 $24 \div (- \frac{1}{3}) - 3^{2} \times {(- 2)}^{3}$

查看试题解析
20. 解方程：

(1)、 $x - 2 (x - 4) = 3$

(2)、 $1 - \frac{3 x - 1}{4} = \frac{x}{2}$

查看试题解析
21. 先化简，再求值： $8 x^{2} y - 2 (3 x^{2} y - x y) - x y$ ，其中， $x = - 3 ， y = 2$ .

查看试题解析
22. 某志愿者驾驶汽车在东西走向的道路上来回的运输防疫物资.若约定向东行驶记为正，已知某天他从道路上的A地出发到运输物资结束的行驶记录如下（单位：千米）；
$＋ 12 ，－ 3 ，＋ 5 ，－ 2 ，－ 6 ，－ 10 ．$

(1)、运输物资结束时，汽车停在A地哪一边，距离A地多远？

(2)、若汽车的耗油量为0.1升每千米，求这天汽车运输物资耗油多少升？

查看试题解析
23. 某口罩生产企业第一车间有工人150名，第二车间工人数比第一车间的 $\frac{4}{5}$ 多10人.

(1)、求第二车间工人数；

(2)、现因生产需要，给两个车间都增加了工人，已知第二车间增加的工人数是第一车间增加的工人数的2倍，若此时第二车间工人数比第一车间多10人，求第一车间增加的工人数.

查看试题解析
24. 如图，已知 $∠ A O B = 110 °$ ， $O C$ 在 $∠ A O B$ 内部， $O D$ 在 $∠ B O C$ 的内部， $∠ C O D = 40 °$ .

(1)、若 $∠ A O C = 50 °$ ，则 $∠ B O D =$ ；若 $∠ A O C = x °$ ，则 $∠ B O D =$ （用含 $x$ 的代数式表示）；

(2)、若 $∠ A O D = 2 ∠ B O C$ ，求 $∠ A O C$ 的度数；

(3)、将 $∠ A O C$ 以OC为折痕进行翻折， $O A$ 落在 $O E$ 处，将 $∠ B O D$ 以 $O D$ 为折痕进行翻折， $O B$ 落在 $O F$ 处， $∠ A O C$ 的度数变化时， $∠ E O F$ 的度数是否发生变化？若变化，请说明理由：若不变，请求出 $∠ E O F$ 的度数.

查看试题解析