浙江省金华市武义县2022-2023学年七年级上学期期末数学试题

试卷更新日期：2023-03-08 类型：期末考试

进入出卷网下载

一、单选题

1. －5的倒数是

A、 $\frac{1}{5}$ B、5 C、 $- \frac{1}{5}$ D、－5

查看试题解析
2. 2022年11月20日晚，卡塔尔世界杯正式开幕，仅两天时间，抖音“世界杯”总话题播放量高达21480000000次，其中数21480000000用科学记数法表示为（）

A、 $214.8 \times 1 0^{8}$ B、 $21.48 \times 1 0^{8}$ C、 $2.148 \times 1 0^{9}$ D、 $2.148 \times 1 0^{10}$

查看试题解析
3. 将一根木条固定在墙上至少需要两枚钉子，这一生活经验运用到的数学知识是（）

A、两点确定一条直线 B、两点之间线段最短 C、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线 D、连结直线外一点与直线上各点的所有连线中，垂线段最短

查看试题解析
4. 如果 $3 a^{m + 3} b^{4}$ 与 $a^{2} b^{n}$ 是同类项，则 $m n$ 的值为（）

A、4 B、-4 C、8 D、12

查看试题解析
5. 如图，数轴上点M表示的数可能是（）

A、 $\sqrt{2}$ B、 $\sqrt{5}$ C、 $\sqrt{8}$ D、 $\sqrt{10}$

查看试题解析
6. 在生产图纸上通常用 $\emptyset 30 0_{- 0.5}^{+ 0.2}$ 来表示轴的加工要求，这里 $\emptyset 300$ 表示直径是 $300 m m$ ， $+ 0.2$ 和 $- 0.5$ 是指直径在 $(300 - 0.5) m m$ 到 $(300 + 0.2) m m$ 之间的产品都属于合格产品.现加工一批轴，尺寸要求是 $\emptyset 4 5_{- 0.3}^{+ 0.2}$ ，则下面产品合格的是（）

A、 $44.6 m m$ B、 $44.8 m m$ C、 $45.3 m m$ D、 $45.5 m m$

查看试题解析
7. 把方程 $\frac{2 x - 1}{4} = 2 - \frac{x + 1}{8}$ 作去分母变形，结果正确的是（）

A、 $2 x - 1 = 2 - (x + 1)$ B、 $2 (2 x - 1) = 2 - (x + 1)$ C、 $2 (2 x - 1) = 16 - x + 1$ D、 $2 (2 x - 1) = 16 - (x + 1)$

查看试题解析
8. 下列各组数中，互为相反数的是（）

A、 $- \sqrt{9}$ 与 $\sqrt[3]{27}$ B、 $\sqrt[3]{- 8}$ 与 $- \sqrt[3]{8}$ C、 $| - \sqrt{2} |$ 与 $\sqrt{2}$ D、 $\sqrt{2}$ 与 $\sqrt[3]{- 8}$

查看试题解析
9. 一张纸的厚度为0.09mm，假设连续对折始终都是可能的，那么至少对折n次后，所得的厚度可以超过厚度为0.9cm的数学课本.则n的值为（）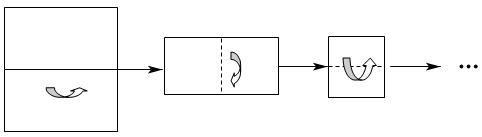

A、5 B、6 C、7 D、8

查看试题解析
10. 钟表上从早上6点30分到早上8点10分时针所走的度数为（）

A、45° B、50° C、55° D、60°

查看试题解析

二、填空题

11. 比较两个数的大小：0 $- 5$ .

查看试题解析
12. 要做一个体积为 $8 c m^{3}$ 的立方体模型（如图），它的棱长为 $c m$ .

查看试题解析
13. 已知 $a + b = 8$ ，则代数式 $1 - 2 a - 2 b$ 的值为.

查看试题解析
14. 如图，点C，M，N在线段AB上， $A C = 12 ， B C = 6 ， A M = \frac{1}{3} A C ， B N = \frac{1}{3} B C$ .则线段MN的长为.

查看试题解析
15. 如图，小红同学编了一道数学谜题，若设“□”内的数字为x，则可列出方程为.

查看试题解析
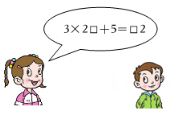16. 因疫情防控需要，一辆货车在早上8：00从甲地出发运送防疫物资到距离 $330 k m$ 乙地， $t (h)$ 后货车到达离甲地 $90 k m$ 的服务区休息，此时一辆轿车正从甲地急送防疫专家到乙地.10：00货车以原来的速度继续行驶，11：00轿车在距离甲地 $150 k m$ 处追上了货车，两车继续向乙地行驶.

(1)、货车的速度是 $k m / h$ .

(2)、轿车比货车早 $h$ 到达乙地.

查看试题解析

三、解答题

17. 计算：

(1)、 $4 - (- 2) + (- 6)$

(2)、 $42 \div (- 5) \times (- \frac{5}{7})$

查看试题解析
18. 计算： $6 \times (\frac{1}{2} - ■) + 2$ .
圆圆在做作业时，发现题中有一个数字被墨水污染了.

(1)、如果被污染的数字是 $\frac{4}{3}$ ，请计算 $6 \times (\frac{1}{2} - \frac{4}{3}) + 2$ .

(2)、如果计算结果等于14，求被污染的数字.

查看试题解析
19. 先化简再求值： $2 (a^{2} b - 2 a b) - 3 (a^{2} b - 3 a b) + a^{2} b$ ，其中 $a = - 2 ， b = \frac{1}{5}$ .

查看试题解析
20. 植树节，小明种树棵数是小聪种树棵数的1.2倍，小慧种树棵数是小明种树棵数的一半少5棵，三人一共种树23棵.设小聪种了x棵树.

(1)、小明种树棵，小慧种树棵（用含x的代数式表示）.

(2)、请求出小聪种树的棵树.

查看试题解析
21. 如图，两叠规格相同的杯子整齐地叠放在桌面上，请根据图中给出的数据信息，解答下列问题：

(1)、按如图所示叠放一起时，相邻两个杯子杯口之间的高度相差cm.

(2)、若x个杯子按如图所示整齐叠放在桌面上，求这些杯子的顶部距离桌面的距离（用含x的代数式表示）.当 $x = 10$ 时，求这些杯子的顶部距离桌面的距离.

查看试题解析
22. 如图，已知直线l表示一段公路，点A表示学校，点B表示书店，点C表示图书馆.

⑴请画出学校A到书店B的最短路线.
⑵在公路l上找一个路口M，使得 $A M + C M$ 的值最小.
⑶现要从学校A向公路l修一条小路，怎样修路才能使小路的长最短？请画出小路的路线，并用所学知识描述小路的方向.

查看试题解析
23. 已知一列，数 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， …，具有以下规律： $a_{2 n + 1} = a_{n}$ ， $a_{2 n + 2} = a_{n} + a_{n + 1}$ .
例：若 $a_{0} = 1$ ，则 $a_{1} = a_{2 \times 0 + 1} = a_{0} = 1$ ， $a_{2} = a_{2 \times 0 + 2} = a_{0} + a_{1} = 2 a_{0} = 2$ ，

$a_{3} = a_{2 \times 1 + 1} = a_{1} = a_{0} = 1$ ， $a_{4} = a_{2 \times 1 + 2} = a_{1} + a_{2} = 3 a_{0} = 3$ ，

$a_{5} = a_{2 \times 2 + 1} = a_{2} = 2 a_{0} = 2$ ， …

请认真阅读上面的运算推理过程，完成下面问题.

(1)、若 $a_{0} = - 2$ ，求下列两个问题.
① $a_{3} =$ ， $a_{6} =$ .

②在数轴上点A所表示的数为 $a_{3}$ ，点B所表示的数为 $a_{9}$ ，求线段AB的长.

(2)、已知 $| a_{9} - 3 | + | a_{13} + 2 | = 8$ ，求 $a_{0}$ 的值.

查看试题解析
24. 含有 $45 °$ 的直角三角板 $A B C$ 和含有 $30 °$ 的直角三角板 $B D E$ 按如图1放置， $A B$ 和 $B E$ 重合.

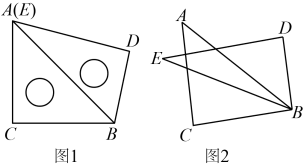
【操作一】三角板 $A B C$ 保持不变，将三角板 $B D E$ 绕着点 $B$ 以每秒 $15 °$ 的速度按逆时针方向旋转.当它完成旋转一周时停止，设旋转的时间为t秒.

(1)、当 $t = 0$ 时， $∠ C B D =$ 度.

(2)、求t为何值时， $B D ⊥ B C$ .
【操作二】如图2，在三角板 $B D E$ 绕着点B以每秒 $15 °$ 的速度按逆时针方向旋转的同时，三角板 $A B C$ 也绕着点B以每秒 $5 °$ 的速度按逆时针方向旋转，设旋转时间为t秒（ $0 < t \leq 18$ ）.

(3)、求t为何值时， $B D$ 与 $A B$ 重合.

(4)、试探索：在两个三角板旋转的过程中，是否存在某个时刻，使得 $∠ A B D$ 与 $∠ A B E$ 中其中一个角是另一个角的两倍？若存在，请求出所有满足题意的t的值；若不存在，请说明理由.

查看试题解析