浙江省金华市金东区2022-2023学年八年级上学期期末检测数学试题

试卷更新日期：2023-03-08 类型：期末考试

进入出卷网下载

一、单选题

1. 篆体是我国汉字古代书体之一．下列篆体字“美”，“丽”，“北”，“京”中，不是轴对称图形的为（）

A、 B、 C、 D、

查看试题解析
2. 不等式 $1 + x < 0$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
3. 下列不等式变形正确的是（）

A、由4x﹣1≥0得4x＞1 B、由5x＞3得x＞3 C、由﹣2x＜4得x＜﹣2 D、由 $\frac{y}{2}$ ＞0得y＞0

查看试题解析
4. 如图，有一块三角形的玻璃，不小心掉在地上打成三块，现要到玻璃店重新划一块与原来形状、大小一样的玻璃，只需带到玻璃店（）

A、① B、② C、③ D、①、②、③其中任一块

查看试题解析
5. 两个小伙伴拿着如图的密码表玩听声音猜动物的游戏，若听到“咚咚－咚咚，咚－咚，咚咚咚－咚”表示的动物是“狗”，则听到“咚咚－咚，咚咚咚－咚咚，咚－咚咚咚”时，表示的动物是（）

A、狐狸 B、猫 C、蜜蜂 D、牛

查看试题解析
6. 在平面直角坐标系中，若点 $P (2 - m ， 7 - 2 m)$ 在第二象限，则整数m的值为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，在等腰三角形 $A B C$ 中， $A D$ 是底边 $B C$ 上的中线， $D E$ 是 $△ A B D$ 高线.图中与 $∠ B A D$ 一定相等的角有（不含本身）（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 直线 $y = k x + 3$ 与 $y = 3 x + k (k < 0)$ 在同一平面直角坐标系内，其位置可能是（）

A、 B、 C、 D、

查看试题解析
9. 为了美化校园，学校决定利用现有的2660盆甲种花卉和 $3000$ 盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内，已知搭配一个A种造型需甲种花卉70盆，乙种花卉 $30$ 盆，搭配一个B种造型需甲种花卉40盆，乙种花卉 $80$ 盆.设搭配A种造型x个，你认为下列符合题意的不等式组是（）

A、 ${\begin{array}{l} 70 x + 40 (50 - x) \leq 2660 \\ 30 x + 80 (50 - x) \leq 3000 \end{array}$ B、 ${\begin{array}{l} 70 x + 40 (50 - x) < 2660 \\ 30 x + 80 (50 - x) < 3000 \end{array}$ C、 ${\begin{array}{l} 70 x + 40 (50 - x) \geq 2660 \\ 30 x + 80 (50 - x) \geq 3000 \end{array}$ D、 ${\begin{array}{l} 70 x + 40 (50 - x) > 2660 \\ 30 x + 80 (50 - x) > 3000 \end{array}$

查看试题解析
10. A，B两地相距640km，甲、乙两辆汽车从A地出发到B地，均匀速行驶，甲出发1小时后，乙出发沿同一路线行驶，设甲、乙两车相距s（km），甲行驶的时间为t（h），s与t的关系如图所示，下列说法：
①甲车行驶的速度是60km/h，乙车行驶的速度是80km/h；②甲出发4h后被乙追上；③甲比乙晚到 $\frac{5}{3} h$ ；④甲车行驶8h或 $9 \frac{1}{4} h$ ，甲，乙两车相距80km；
其中错误的（）

A、序号① B、序号② C、序号③ D、序号④

查看试题解析

二、填空题

11. 不等式 $3 x + 4 \leq 10$ 的解集是.

查看试题解析
12. 命题：直角三角形两条直角边的平方和等于斜边的平方，其逆命题是.

查看试题解析
13. 如图，直线 $A B ∥ C D$ ，且 $A C ⊥ C B$ 于点C，若 $∠ B A C = 35 °$ ，则 $∠ B C D$ 的度数为.

查看试题解析
14. 已知 $1 < x < 2$ ，则 $\sqrt{{(x - 2)}^{2}} + | x - 1 | =$ .

查看试题解析
15. 如图， $△ A B C$ 的三条中线AD，BE，CF交于点O，若 $△ A B C$ 的面积为20，那么阴影部分的面积之和为.

查看试题解析
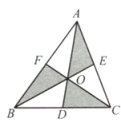16. 小明发现妈妈的耳环设计非常巧妙，如图1所示，其形状像中国数学家赵爽使用的弦图，用该弦图证明勾股定理在数学史上有着重要地位，将耳环中弦图顺时针旋转 $45 °$ 得到如图2图形，若这四个全等的直角三角形都有一个角为 $30 °$ ，且 $A_{1} B_{1} = 2$ ，则 $M_{1} N_{1} P_{1} Q_{1}$ 面积为；将多个弦图如图3摆放，使得顶点 $B_{1}$ ， $B_{2}$ ， $B_{3}$ ， …， $B_{n}$ ， $C_{1}$ ， $C_{2}$ ， $C_{3}$ ， …， $C_{n}$ 分别在直线 $y = - x + 4$ 和x轴上，则正方形 $M_{n} N_{n} P_{n} Q_{n}$ 的面积是.

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} \frac{1}{2} (x + 4) < 2 ① \\ x - 3 (x - 1) > 5 ② \end{array}$

查看试题解析
18. 已知：如图，点B，F，C，E在一条直线上， $∠ B = ∠ E F D$ ， $∠ A C B = ∠ D E F$ ，且 $B F = E C$ .求证： $△ A B C ≌ △ D F E$ .

查看试题解析
19. 在如图所示的方格纸中，
⑴在 $△ A B C$ 中，作BC边上的高AD.
⑵作AC边上的中线BE.
⑶求 $△ A B E$ 的面积.

查看试题解析
20. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F.

(1)、求证：△CEF是等腰三角形；

(2)、若CD＝3，求DF的长.

查看试题解析
21. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ ，垂足为D， $B D = C D$ ，延长 $B C$ 至E.使得 $C E = C A$ ，连接AE.

(1)、求证： $∠ B = ∠ A C B$ .

(2)、若 $A B = 5$ ， $A D = 4$ ，
①求 $△ A B C$ 的面积.
②求 $△ A B E$ 的周长，

查看试题解析
22. 假期将至，金华某旅行社准备打印一些照片进行宣传，某打印店现推出活动如下：“方式A”使用者先交50元会员费，然后每打印一张，再付0.4元；“方式B”免交会员费，每打印一张，付0.6元.若本次打印x张，两种方式的费用分别为 $y_{1}$ 元和 $y_{2}$ 元.

(1)、写出 $y_{1}$ ， $y_{2}$ 与x之间的函数关系式.

(2)、当打印多少张时两种方式的费用相同？并说明相应理由.

(3)、如果此次打印不超过150张，请你为其选一种便宜的打印方式；如果不低于300张，请你为其选种便宜的打印方式.

查看试题解析
23. 定义：三角形一边上的点到三角形的另两条边的距离相等，称此点为这个三角形这边上的雅实心，如：
如图1，当点P在 $△ A B C$ 的 $A C$ 边上时，若 $P D ⊥ B C$ 于点D， $P E ⊥ A B$ 于点E，且 $P D = P E$ ，则称点P为 $△ A B C$ 的 $A C$ 边上的雅实心， $△ A B C$ 各边上的三个雅实心为顶点构成新三角形，叫做 $△ A B C$ 的雅实三角形.

(1)、如图2， $△ A B C$ 中， $A B = A C = 10 c m$ ， $B C = 12 c m$ ，求 $B C$ 边上的雅实心P到 $A B$ 的距离 $P D$ .

(2)、如图3，等边 $△ A B C$ 的边长为 $4 c m$ ，求等边 $△ A B C$ 的雅实三角形的面积.

(3)、如图4，在平面直角坐标系 $x O y$ 中，点A，B分别在x，y轴上，且 $A (2 ， 0)$ ， $∠ B A O = 60 °$ ，求 $△ A O B$ 的斜边上的雅实心P的坐标.

查看试题解析
24. 已知在直角坐标系 $x O y$ 中，点 $A (0 ， 4)$ ， $B (4 ， 0)$ ， $C (0 ， 3)$ ，由线段 $O C$ 绕原点O顺时针转动某个角度得到线段 $O P$ ，线段 $O P$ 顺时针转动 $90 °$ 得到线段 $O Q$ ，连接 $P Q$ ，作直线 $A P ， B Q$ 交于点R.

(1)、如图1，当点P在第一象限
①若 $∠ A O P = 45 °$ 时，求点P坐标；
②求证： $△ A O P ≌ △ B O Q$ ；
③求证： $∠ P R Q = 90 °$ ；

(2)、在线段 $O C$ 绕原点转动的过程中，当 $△ P Q R$ 为等腰三角形时，求点P坐标.

查看试题解析