浙江省湖州市长兴县2022-2023学年九年级上学期期末检测数学试题
试卷更新日期:2023-03-08 类型:期末考试
一、单选题
-
1. 抛物线 的顶点坐标是( )A、(3,1) B、(3,﹣1) C、(﹣3,1) D、(﹣3,﹣1)2. 如果正多边形的一个内角是 ,则这个多边形是( )A、正十边形 B、正九边形 C、正八边形 D、正七边形3. 下列事件中,是必然事件的是( )A、三角形的外心到三边的距离相等 B、任意画一个三角形,其内角和是180° C、射击运动员射击一次,命中靶心 D、经过有交通信号灯的路口,遇到红灯4. 已知扇形的半径为6,圆心角为 , 则此扇形的弧长是( )A、4 B、2 C、 D、5. 如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC相似的是( )
 A、
A、 B、
B、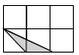 C、
C、 D、
D、 6. 如图,在中,.是的外接圆,为弧的中点,为延长线上一点.若 , 则的度数是( )
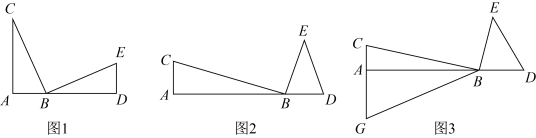
6. 如图,在中,.是的外接圆,为弧的中点,为延长线上一点.若 , 则的度数是( )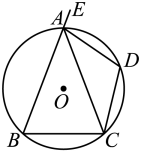 A、 B、 C、 D、7. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形.如果已知 , , 则的值是( )
A、 B、 C、 D、7. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形.如果已知 , , 则的值是( ) A、 B、 C、 D、8. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形中, , 分别是 , 上的格点, , .若点是这个网格图形中的格点,连结 , , 构造 , 使得有一个内角为 , 则满足题意的点的个数是( )
A、 B、 C、 D、8. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形中, , 分别是 , 上的格点, , .若点是这个网格图形中的格点,连结 , , 构造 , 使得有一个内角为 , 则满足题意的点的个数是( )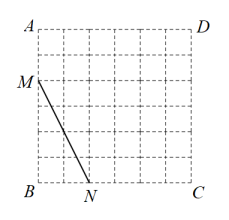 A、5 B、6 C、7 D、89. 如图,抛物线与轴正半轴交于两点(点在点的左边),与轴正半轴交于 , 且 , 则点的坐标是( )
A、5 B、6 C、7 D、89. 如图,抛物线与轴正半轴交于两点(点在点的左边),与轴正半轴交于 , 且 , 则点的坐标是( ) A、 B、 C、 D、10. 在中, , 点是边上的一动点,过点作交边于点 , 过点作交的延长线于点 , 分别以为对角线画矩形和矩形 , 则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( )
A、 B、 C、 D、10. 在中, , 点是边上的一动点,过点作交边于点 , 过点作交的延长线于点 , 分别以为对角线画矩形和矩形 , 则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( ) A、 B、 C、6 D、
A、 B、 C、6 D、二、填空题
-
11. 在中, , 则的值为.12. 若将二次函数的图象向左平移个单位,再向下平移个单位,所得图象的函数表达式为 , 则h=;k=.13. 袋中装有2个黑球和个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为”,则这个袋中白球有个.14. 如图,在一张长方形纸片中, 点 , 分别是和的中点,点是上一点,将矩形的一角沿所在的直线翻折,点恰好落在上,若 , 则的长是.
 15. 如图,将二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象,当直线与新图象有4个交点时,m的取值范围是.
15. 如图,将二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象,当直线与新图象有4个交点时,m的取值范围是. 16. ⊙为等边的外接圆,半径为2,点在劣弧上运动(不与点 , 重合),连结 , , .则四边形的面积关于线段的长的函数解析式是.
16. ⊙为等边的外接圆,半径为2,点在劣弧上运动(不与点 , 重合),连结 , , .则四边形的面积关于线段的长的函数解析式是.
三、解答题
-
17. 已知 , 求下列算式的值.(1)、.(2)、.18. 已知二次函数图象的顶点坐标是 , 且经过点.(1)、求这个二次函数的表达式;(2)、若点在该函数图象上,求点B的坐标.19. 某县为创评“全国文明城市”称号,周末团县委组织志愿者进行宣传活动.班主任周老师决定从4名女班干部(小兰,小红,小丽和小倩)中通过抽签方式确定2名女生去参加.抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,周老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.(1)、第一次抽取卡片“小红被抽中”的概率为;(2)、用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小丽被抽中”的概率.20. 为加快城乡对接,建设美丽乡村,某地区对A、B两地间的公路进行改建,如图,A,B两地之间有一座山.汽车原来从A地到B地需途经C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶,已知BC=80千米,∠A=45°,∠B=30°.
 (1)、开通隧道前,汽车从A地到B地要走多少千米?(2)、开通隧道后,汽车从A地到B地可以少走多少千米?(结果保留根号)21. 如图,为的直径,点在上,延长至点 , 使.延长与的另一个交点为 , 连结.
(1)、开通隧道前,汽车从A地到B地要走多少千米?(2)、开通隧道后,汽车从A地到B地可以少走多少千米?(结果保留根号)21. 如图,为的直径,点在上,延长至点 , 使.延长与的另一个交点为 , 连结. (1)、求证:;(2)、若 , 求的长.22. 如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球 门的横梁高OA为2.44m.
(1)、求证:;(2)、若 , 求的长.22. 如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球 门的横梁高OA为2.44m.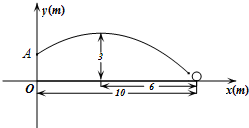 (1)、在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)(2)、守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
(1)、在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)(2)、守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?