浙江省杭州市西湖区2022-2023学年九年级上学期期末教学质量调研数学试题卷
试卷更新日期:2023-03-08 类型:期末考试
一、单选题
-
1. 若(a,b均不为0),则的值是( )A、2 B、3 C、2:3 D、3:22. 已知是半径为2的圆的一条弦,则的长可能是( )A、4 B、5 C、6 D、73. 在一个边长为1的正方形中挖去一个边长为的小正方形,如果设剩余部分的面积为y,那么y关于x的函数表达式为( )A、 B、 C、 D、4. 从甲、乙、丙三人中任选两人参加青年志愿者活动,甲被选中的概率是( )A、 B、 C、 D、5. 如图,能使成立的条件是( )
 A、 B、 C、 D、6. 若点Р是线段的黄金分割点 , , 则的长为( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,以点为旋转中心,将点按逆时针方向旋转到点B,点B在y轴上,则扇形AOB的面积为( )
A、 B、 C、 D、6. 若点Р是线段的黄金分割点 , , 则的长为( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,以点为旋转中心,将点按逆时针方向旋转到点B,点B在y轴上,则扇形AOB的面积为( )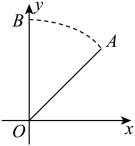 A、 B、 C、 D、8. 已知二次函数 , 函数值与自变量的部分对应值如表:
A、 B、 C、 D、8. 已知二次函数 , 函数值与自变量的部分对应值如表:-1
0
1
2
3
18
8
2
0
2
则当时,的取值范围是( )
A、 B、 C、或 D、或9. 如图,E,F,G,H分别是矩形四条边上的点,已知 , 若 , , 则为( )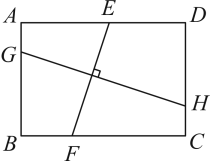 A、 B、 C、 D、10. 设函数 , .直线的图象与函数 , 的图象分别交于点 , , 得( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
A、 B、 C、 D、10. 设函数 , .直线的图象与函数 , 的图象分别交于点 , , 得( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则二、填空题
-
11. 二次函数图象与轴的交点坐标为.12. 在一个不透明的袋中装有一些除颜色外完全相同的红和黑两种颜色的小球,已知袋中有红球5个,黑球个,从袋中随机摸出一个红球的概率是 , 则的值为.13. 如图,为的直径,点C在上,点Р在线段上运动(不与O,B重合),若 , 设为 , 则的取值范围是.
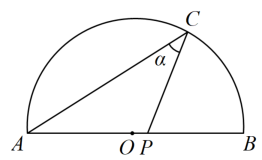 14. 如图,用一个半径为6cm的定滑轮拉动砝码上升(假设绳索足够长且粗细不计,与滑轮之间无滑动),若滑轮旋转了 , 则砝码上升了cm.(结果保留)
14. 如图,用一个半径为6cm的定滑轮拉动砝码上升(假设绳索足够长且粗细不计,与滑轮之间无滑动),若滑轮旋转了 , 则砝码上升了cm.(结果保留) 15. 对于二次函数和 , 其自变量和函数值的两组对应值如表所示(其中a、b均不为0,),根据二次函数图象的相关性质可知: , .
15. 对于二次函数和 , 其自变量和函数值的两组对应值如表所示(其中a、b均不为0,),根据二次函数图象的相关性质可知: , .1
16. 如图,线段是的直径,弦于点H,点是弧上任意一点(不与B,C重合), , .延长线段交的延长线于点E,直线交于点N,连结交于点F,则 , .
三、解答题
-
17. 已知 , 请写出一个二次函数同时满足以下两个条件:
①与函数图象开口大小、方向相同;
②当时,y随x的增大而增大.
18. 一个不透明的袋中装有2个白球,1个红球.这些球除颜色外,没有任何其他区别,有如下两个活动:活动1:从袋中随机摸出一个球,记下颜色,然后从袋中剩余的球中再随机摸出一个球,摸出的两个球都是白球的概率记为;
活动2:从袋中随机摸出一个球,记下颜色,然后把这个球放回袋中并摇匀,重新从袋中随机摸出一个球,两次摸出的球都是白球的概率记为.
试猜想 , 的大小关系,并用画树状图或列表的方法列出所有可能的结果,验证你的猜想.
19. 如图,在中,于点D,点E在上(不与点A,B重合),连接交于点F,. (1)、求证:.(2)、若 , , , 求的长.20. 在平面直角坐标系中,二次函数的图象经过点.(1)、求的值.(2)、若二次函数的顶点为 , 求的最大值.
(1)、求证:.(2)、若 , , , 求的长.20. 在平面直角坐标系中,二次函数的图象经过点.(1)、求的值.(2)、若二次函数的顶点为 , 求的最大值.

