浙江省杭州市富阳区2022-2023学年九年级上学期期末学业水平测试数学试题
试卷更新日期:2023-03-08 类型:期末考试
一、单选题
-
1. 的值等于( )A、 B、 C、1 D、2. 下列事件中,属于随机事件的是( )A、从地面向上抛的硬币会落下 B、射击运动员射击一次,命中10环 C、太阳从东边升起 D、有一匹马奔跑的速度是70米/秒3. 如图,线段 , 相交于点 , , 若 , , , 则的长是( )
 A、3 B、4 C、5 D、64. 一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )A、2π B、4π C、12π D、24π5. 如图所示,将一个含角的直角三角板绕点逆时针旋转,点的对应点是点 , 若点、、在同一条直线上,则三角板旋转的度数是( )
A、3 B、4 C、5 D、64. 一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )A、2π B、4π C、12π D、24π5. 如图所示,将一个含角的直角三角板绕点逆时针旋转,点的对应点是点 , 若点、、在同一条直线上,则三角板旋转的度数是( ) A、 B、 C、 D、6. 关于抛物线 , 下列说法:①图象开口向上;②图象与轴有两个交点;③当时,有最小值-4.正确的是( )A、①② B、①③ C、②③ D、①②③7. 如图,是的直径,是上任意一点(不与 , 重合),设 , , 所对的边分别为 , , , 则( )
A、 B、 C、 D、6. 关于抛物线 , 下列说法:①图象开口向上;②图象与轴有两个交点;③当时,有最小值-4.正确的是( )A、①② B、①③ C、②③ D、①②③7. 如图,是的直径,是上任意一点(不与 , 重合),设 , , 所对的边分别为 , , , 则( ) A、 B、 C、 D、8. 凸透镜成像的原理如图所示,.若物体到焦点的距离与焦点到凸透镜中心线的距离之比为 , 则物体被缩小到原来的( )
A、 B、 C、 D、8. 凸透镜成像的原理如图所示,.若物体到焦点的距离与焦点到凸透镜中心线的距离之比为 , 则物体被缩小到原来的( ) A、 B、 C、 D、9. 已知点 , 在二次函数的图像上,若 , 则必有( )A、 B、 C、 D、10. 计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比,下面是同一个任务进行到不同阶段时进度条的示意图:
A、 B、 C、 D、9. 已知点 , 在二次函数的图像上,若 , 则必有( )A、 B、 C、 D、10. 计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比,下面是同一个任务进行到不同阶段时进度条的示意图:
当任务完成的百分比为时,线段的长度记为.下列描述正确的是( )
A、当时, B、当时, C、当时, D、当时,二、填空题
-
11. 若 , 则.12. 如图,四边形的顶点、、在上,若 , 则.
 13. 学校组织秋游,安排给九年级3辆车,小明和小慧都可以从这3辆车中任选一辆搭乘.则小明和小慧同车的概率为.14. 如图,把两张宽度都是 的纸条交错地叠在一起,相交成角 ,则重叠部分的面积是 .
13. 学校组织秋游,安排给九年级3辆车,小明和小慧都可以从这3辆车中任选一辆搭乘.则小明和小慧同车的概率为.14. 如图,把两张宽度都是 的纸条交错地叠在一起,相交成角 ,则重叠部分的面积是 . 15. 汽车刹车后行驶的距离单位:关于行驶的时间单位:的函数解析式是 , 汽车刹车后到停下来前进了米.16. 如图,面积为4的正方形中,分别是各边的中点,将一边两端点分别和对边中点连结,所得阴影部分为各边相等的八边形,则八边形每条边的长度是.
15. 汽车刹车后行驶的距离单位:关于行驶的时间单位:的函数解析式是 , 汽车刹车后到停下来前进了米.16. 如图,面积为4的正方形中,分别是各边的中点,将一边两端点分别和对边中点连结,所得阴影部分为各边相等的八边形,则八边形每条边的长度是.
三、解答题
-
17. 对一批衬衣进行抽检,统计合格衬衣的件数,得到合格衬衣的频数表如下:
抽取件数(件)
50
100
200
500
800
1000
合格频数
47
95
188
480
763
949
合格频率
0.94
0.95
0.94
0.96
0.95
0.95
(1)、估计任抽一件衬衣是合格品的概率(结果精确到0.01);(2)、估计出售2000件衬衣,其中次品大约有几件.18. 如图, , 交于点 , , 是半径,且于点. (1)、求证:;(2)、若 , , 求的半径.19. 一运动员推铅球,铅球经过的路线为如图所示的抛物线.求铅球的落地点离运动员有多远(结果保留根号)?
(1)、求证:;(2)、若 , , 求的半径.19. 一运动员推铅球,铅球经过的路线为如图所示的抛物线.求铅球的落地点离运动员有多远(结果保留根号)?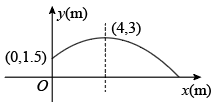 20. 如图,从甲楼底部处测得乙楼顶部处的仰角是 , 从甲楼顶部处测得乙楼顶部处的俯角是 , 已知两楼之间的距离 , 求这两幢楼的高度(结果保留根号).
20. 如图,从甲楼底部处测得乙楼顶部处的仰角是 , 从甲楼顶部处测得乙楼顶部处的俯角是 , 已知两楼之间的距离 , 求这两幢楼的高度(结果保留根号).

