浙江省杭州市滨江区2022—2023学年九年级上学期数学期末考试卷
试卷更新日期:2023-03-08 类型:期末考试
一、单选题
-
1. “明天下雨”这个事件是( )A、确定事件 B、必然事件 C、不可能事件 D、不确定事件2. 已知 , 则下列式子中正确的是( )A、 B、 C、 D、3. 将抛物线向右平移2个单位,再向上平移2个单位,则所得的抛物线的函数表达式为( )A、 B、 C、 D、4. 已知一个扇形的面积是 , 弧长是 , 则这个扇形的半径为( )A、24 B、22 C、12 D、65. 已知二次函数(为实数,且),当时,随增大而减小,则实数的取值范围是( )A、 B、 C、 D、6. 如图,在中,点是上一点,若 , 则的度数为( )
 A、 B、 C、 D、7. 如图,在中, , 边 , 上的中线 , 相交于点 , 若 , , 则( )
A、 B、 C、 D、7. 如图,在中, , 边 , 上的中线 , 相交于点 , 若 , , 则( ) A、 B、 C、 D、8. 如图,在中,点 , 分别在 , 上, , , 且 , , 则的长为( )
A、 B、 C、 D、8. 如图,在中,点 , 分别在 , 上, , , 且 , , 则的长为( ) A、 B、4 C、5 D、9. 如图,内接于 , 且 , 的延长线交于点 , 若与相似,则( ).
A、 B、4 C、5 D、9. 如图,内接于 , 且 , 的延长线交于点 , 若与相似,则( ). A、 B、 C、 D、10. 二次函数(为实数,且),对于满足的任意一个的值,都有 , 则的最大值为( )A、 B、 C、2 D、
A、 B、 C、 D、10. 二次函数(为实数,且),对于满足的任意一个的值,都有 , 则的最大值为( )A、 B、 C、2 D、二、填空题
-
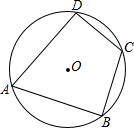
11. 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是.
 12. 做任意抛掷一只纸杯的重复试验,获得如下表数据:
12. 做任意抛掷一只纸杯的重复试验,获得如下表数据:抛掷总次数
100
200
300
400
杯口朝上频数
20
42
66
88
杯口朝上频率
0.2
0.21
0.22
0.22
则估计任意抛掷一只纸杯杯口朝上的概率约为(结果精确到0.01).
13. 如图,正内接于 , 的半径为10,则的弧长为. 14. 已知一个二次函数图象的形状与抛物线相同,它的顶点坐标为 , 则该二次函数的表达式为.15. 如图,矩形的对角线 , 相交于点 , 过点作 , 交于点 , 若 , , 则的长为.
14. 已知一个二次函数图象的形状与抛物线相同,它的顶点坐标为 , 则该二次函数的表达式为.15. 如图,矩形的对角线 , 相交于点 , 过点作 , 交于点 , 若 , , 则的长为.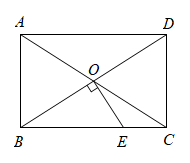 16. 如图,正五边形的对角线和分别交对角线于点 , , 若的面积为 , 则正五边形的面积为(结果用含的代数式表示).
16. 如图,正五边形的对角线和分别交对角线于点 , , 若的面积为 , 则正五边形的面积为(结果用含的代数式表示).
三、解答题
-
17. 一个布袋里装有只有颜色不同的3个球,其中2个红球,1个白球.(1)、从中任意摸出一个球,求摸出的是红球的概率.(2)、从中任意摸出一个球,记下颜色后放回,搅匀,再摸出一个球,请画出树状图或列表,并求摸出的2个球中,1个是白球,1个是红球的概率.18. 如图是一个管道的横截面,圆心到水面的距离是3,水面宽.
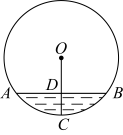 (1)、求这个管道横截面的半径.(2)、求的度数.19. 如图,把一个矩形划分成三个全等的小矩形.
(1)、求这个管道横截面的半径.(2)、求的度数.19. 如图,把一个矩形划分成三个全等的小矩形. (1)、若原矩形的长 , 宽.问:每个小矩形与原矩形相似吗?请说明理由.(2)、若原矩形的长 , 宽 , 且每个小矩形与原矩形相似,求矩形长与宽应满足的关系式.20. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为6 , 桥洞的跨度为12 , 如图建立直角坐标系.
(1)、若原矩形的长 , 宽.问:每个小矩形与原矩形相似吗?请说明理由.(2)、若原矩形的长 , 宽 , 且每个小矩形与原矩形相似,求矩形长与宽应满足的关系式.20. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为6 , 桥洞的跨度为12 , 如图建立直角坐标系. (1)、求这条抛物线的函数表达式.(2)、求离对称轴2处,桥洞离水面的高是多少?
(1)、求这条抛物线的函数表达式.(2)、求离对称轴2处,桥洞离水面的高是多少?