四川省成都市青羊区2023年一诊数学试题
试卷更新日期:2023-03-08 类型:中考模拟
一、单选题
-
1. 如图是由5个相同的正方体搭成的几何体,这个几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 下列各式计算正确的是( )A、 B、 C、 D、4. 在一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在20%附近,则口袋中白球可能有( )A、5个 B、6个 C、7个 D、8个5. 若点 , , 在反比例函数的图象上,则、、的大小关系是( )A、 B、 C、 D、6.
2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 下列各式计算正确的是( )A、 B、 C、 D、4. 在一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在20%附近,则口袋中白球可能有( )A、5个 B、6个 C、7个 D、8个5. 若点 , , 在反比例函数的图象上,则、、的大小关系是( )A、 B、 C、 D、6.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
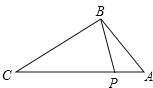 A、∠ABP=∠C B、∠APB=∠ABC C、 D、7. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )
A、∠ABP=∠C B、∠APB=∠ABC C、 D、7. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )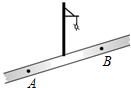 A、
A、 B、
B、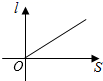 C、
C、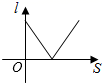 D、
D、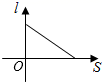 8. 下列说法中,正确的是( )A、有一个角是直角的平行四边形是正方形 B、对角线相等的四边形是矩形 C、对角线互相垂直平分的四边形是菱形 D、一组对边平行,另一组对边相等的四边形是平行四边形
8. 下列说法中,正确的是( )A、有一个角是直角的平行四边形是正方形 B、对角线相等的四边形是矩形 C、对角线互相垂直平分的四边形是菱形 D、一组对边平行,另一组对边相等的四边形是平行四边形二、填空题
-
9. 比较大小:.(填“>”,“<”,或“=”)10. 如图,已知为反比例函数的图像上一点,过点作轴,垂足为.若的面积为3,则的值为.
 11. 如图,在中, , 点D为边上一点,连接.现将沿翻折使得点A落在边的中点E处.若 , 则.
11. 如图,在中, , 点D为边上一点,连接.现将沿翻折使得点A落在边的中点E处.若 , 则. 12. 化简:.13. 如图,在中, , 分别以C、B为圆心,取的长为半径作弧,两弧交于点D.连接、.若 , 则.
12. 化简:.13. 如图,在中, , 分别以C、B为圆心,取的长为半径作弧,两弧交于点D.连接、.若 , 则.
三、解答题
-
14. 按要求解答下列各题:(1)、计算:;(2)、解方程:.15. 如图,在平面直角坐标系中,的顶点坐标分别为 , , (每个方格的边长均为1个单位长度).
 (1)、将先向左平移4个单位,再向上平移1个单位后得到 , 请在平面直角坐标系中画出平移后的.(2)、请以O为位似中心,在y轴右侧画出的位似图形 , 使与的相似比为 , 则点的坐标为( ▲ , ▲ );点的坐标为( ▲ , ▲ ).16. 成都市某旅游机构抽样调查了外地游客对A、B、C、D四个景点作为最佳旅游景点的喜爱情况,并将调查情况绘制成如图两幅不完整统计图:
(1)、将先向左平移4个单位,再向上平移1个单位后得到 , 请在平面直角坐标系中画出平移后的.(2)、请以O为位似中心,在y轴右侧画出的位似图形 , 使与的相似比为 , 则点的坐标为( ▲ , ▲ );点的坐标为( ▲ , ▲ ).16. 成都市某旅游机构抽样调查了外地游客对A、B、C、D四个景点作为最佳旅游景点的喜爱情况,并将调查情况绘制成如图两幅不完整统计图: (1)、本次参加抽样调查的游客有 ▲ 人,根据题中信息补全条形统计图.(2)、若某批次游客有6000人,请你估计选择D作为最佳旅游景点的有人.(3)、A旅游景点举行游客有奖问答活动.现有2男2女4名游客回答对了问题.现从4名游客中随机抽取2名游客发放纪念品,请用列表或画树状图的方法求获得此次纪念品的是一男一女的概率.17. 如图,在中, , 点O、C分别是、边的中点.过点D作交的延长线于点A,连接、.
(1)、本次参加抽样调查的游客有 ▲ 人,根据题中信息补全条形统计图.(2)、若某批次游客有6000人,请你估计选择D作为最佳旅游景点的有人.(3)、A旅游景点举行游客有奖问答活动.现有2男2女4名游客回答对了问题.现从4名游客中随机抽取2名游客发放纪念品,请用列表或画树状图的方法求获得此次纪念品的是一男一女的概率.17. 如图,在中, , 点O、C分别是、边的中点.过点D作交的延长线于点A,连接、. (1)、求证:四边形是菱形;(2)、若 , , 求的面积.18. 已知一次函数与反比例函数的图象交于、B两点,交y轴于点C.
(1)、求证:四边形是菱形;(2)、若 , , 求的面积.18. 已知一次函数与反比例函数的图象交于、B两点,交y轴于点C.
 (1)、求反比例函数的表达式和点B的坐标;(2)、过点C的直线交x轴于点E,且与反比例函数图象只有一个交点,求CE的长;(3)、我们把一组邻边垂直且相等,一条对角线平分另一条对角线的四边形叫做“维纳斯四边形”.设点P是y轴负半轴上一点,点Q是第一象限内的反比例函数图象上一点,当四边形是“维纳斯四边形”时,求Q点的横坐标的值.
(1)、求反比例函数的表达式和点B的坐标;(2)、过点C的直线交x轴于点E,且与反比例函数图象只有一个交点,求CE的长;(3)、我们把一组邻边垂直且相等,一条对角线平分另一条对角线的四边形叫做“维纳斯四边形”.设点P是y轴负半轴上一点,点Q是第一象限内的反比例函数图象上一点,当四边形是“维纳斯四边形”时,求Q点的横坐标的值.四、填空题
-
19. 已知点C是线段AB的黄金分割点(靠近A),AB=2,则BC= .20. 一个密码锁的密码由四个数字组成,每个数字都是这十个数字中的一个,只有当四个数字与所设定的密码相同时,才能将锁打开,粗心的小张忘记了后两个数字,他一次就能打开该锁的概率是.21. 已知、是关于x的一元二次方程的两个实数根.若 , 则.22. 如图,正比例函数与反比例函数的图像交于点A,另有一次函数与、图像分别交于B、C两点(点C在直线的上方),且 , 则.
 23. 已知矩形中, , 点E、F分别是边的中点,点P为边上动点,过点P作与平行的直线交于点G,连接 , 点M是中点,连接 , 则的最小值=.
23. 已知矩形中, , 点E、F分别是边的中点,点P为边上动点,过点P作与平行的直线交于点G,连接 , 点M是中点,连接 , 则的最小值=.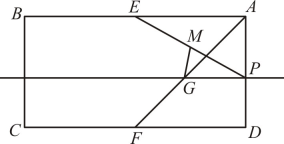
五、解答题
-
24. 新华商场销售某种彩电,每台进价为3500元,调查发现,当销售价为3900元时,平均每天能售出8台,而当销售价每降低75元,平均每天能多卖6台.(1)、若每台彩电降价x元,则每天彩电的销量为多少?(请用含有x的式子表示)(2)、商场要想使这种彩电的销售利润平均每天达到5000元,则每台彩电应降价多少元?


