陕西省榆林市2023年中考数学第一次模拟考试卷
试卷更新日期:2023-03-08 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、3 B、-3 C、 D、12. 如图将一块三角板如图放置, ,点 分别在 上,若 ,则 的度数为( )
 A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 添加下列一个条件,能使矩形成为正方形的是( )A、 B、 C、 D、5. 四边形不具稳定性,四条边长都确定的四边形.当内角的大小发生变化时.其形状也随之改变.如图,改变正方形 的内角,使正方形 变为菱形 ,如果 ,那么菱形 与正方形 的面积之比是( )
A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 添加下列一个条件,能使矩形成为正方形的是( )A、 B、 C、 D、5. 四边形不具稳定性,四条边长都确定的四边形.当内角的大小发生变化时.其形状也随之改变.如图,改变正方形 的内角,使正方形 变为菱形 ,如果 ,那么菱形 与正方形 的面积之比是( ) A、 B、 C、 D、16. 如图,一次函数与的图象相交于点 , 则关于 , 的二元方程组的解是( )
A、 B、 C、 D、16. 如图,一次函数与的图象相交于点 , 则关于 , 的二元方程组的解是( ) A、 B、 C、 D、7. 已知等腰中, , 则的度数为( )A、 B、 C、或 D、或或8. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、
A、 B、 C、 D、7. 已知等腰中, , 则的度数为( )A、 B、 C、或 D、或或8. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、二、填空题
-
9. 计算:.10. 已知a、b、c在数轴上的位置如图所示,化简:
 11. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.按此比例设计一座高度为3米的雷锋雕像,那么该雕像的下部设计高度约是米.(结果精确到0.1米)12. 若关于x的一元二次方程有一个根是1,则m的值为 .13. 如图,在矩形中, , 点E、F分别在边上,点M为线段上一动点,过点M作的垂线分别交边于点G点H.若线段恰好平分矩形的面积,且 , 则的长为 .
11. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.按此比例设计一座高度为3米的雷锋雕像,那么该雕像的下部设计高度约是米.(结果精确到0.1米)12. 若关于x的一元二次方程有一个根是1,则m的值为 .13. 如图,在矩形中, , 点E、F分别在边上,点M为线段上一动点,过点M作的垂线分别交边于点G点H.若线段恰好平分矩形的面积,且 , 则的长为 .
三、解答题
-
14. 计算:15. 解不等式组并写出该不等式组的最小整数解.16. 化简:.17. 如图, , , , 在同一条直线上,于点 , 于点 , , , 求证:.
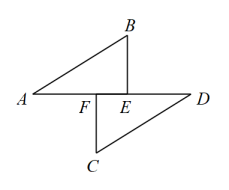 18. 如图,在中, , D、E分别为、上一点,.若 , 求证:.
18. 如图,在中, , D、E分别为、上一点,.若 , 求证:.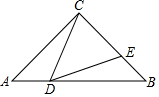 19. 如图,在正方形网格中,每个小正方形的边长为1,格点的顶点A,B的坐标分别为 , .
19. 如图,在正方形网格中,每个小正方形的边长为1,格点的顶点A,B的坐标分别为 , .
⑴请在图中建立适当的直角坐标系.
⑵画出关于x轴对称的 , 并直接写出点的坐标.
20. 一个不透明的口袋里装有分别标有汉字“阳”、“过”、“阳”、“康”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.(1)、从中任取一个球,球上的汉字刚好是“康”的概率为;(2)、甲从中取出两个球,请用列表或画树状图的方法,求出甲取出的两个球上的汉字一个是“阳”一个是“康”的概率.21. 某数学兴趣小组决定利用所学知识测量一古建筑的高度.如图2,古建筑的高度为 , 在地面上取E,G两点,分别竖立两根高为的标杆和 , 两标杆间隔为 , 并且古建筑 , 标杆和在同一竖直平面内.从标杆后退到D处(即),从D处观察A点,A、F、D三点成一线;从标杆后退到C处(即),从C处观察A点,A、H、C三点也成一线.已知B、E、D、G、C在同一直线上, , , , 请你根据以上测量数据,帮助兴趣小组求出该古建筑的高度. 22. 如图1,小明家、食堂、图书馆在同一条直线上,小明从食堂吃完早餐,接着骑自行车去图书馆读书,然后以相同的速度原路返回家.如图2中反映了小明离家的距离与他所用时间之间的函数关系.
22. 如图1,小明家、食堂、图书馆在同一条直线上,小明从食堂吃完早餐,接着骑自行车去图书馆读书,然后以相同的速度原路返回家.如图2中反映了小明离家的距离与他所用时间之间的函数关系.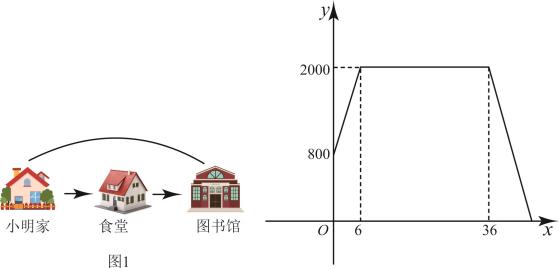 (1)、小明家与图书馆的距离为 , 小明骑自行车速度为;(2)、求小明从图书馆返回家的过程中,与的函数解析式;(3)、当小明离家的距离为时,求的值.23. 为了解学生参加体育锻炼活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育锻炼活动的时间是多少?”共有4个选项:
(1)、小明家与图书馆的距离为 , 小明骑自行车速度为;(2)、求小明从图书馆返回家的过程中,与的函数解析式;(3)、当小明离家的距离为时,求的值.23. 为了解学生参加体育锻炼活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育锻炼活动的时间是多少?”共有4个选项:A.1.5小时以上;B.1~1.5小时;C.0.5~1小时;D.0.5小时以下.
请你根据统计图提供的信息,解答以下问题:
 (1)、本次一共调查了多少名学生?(2)、在条形统计图中将选项B的部分补充完整;(3)、若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育锻炼的时间在0.5小时以下.24. 如图,在中, , 若点P从点A出发,以每秒的速度沿折线运动,设运动时间为t秒
(1)、本次一共调查了多少名学生?(2)、在条形统计图中将选项B的部分补充完整;(3)、若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育锻炼的时间在0.5小时以下.24. 如图,在中, , 若点P从点A出发,以每秒的速度沿折线运动,设运动时间为t秒
备用图1 备用图2
(1)、若点P在上,且满足的周长为 , 则t的值为;(2)、若点P在的平分线上,求此时t的值;(3)、运动过程中,直接写出当t为何值时,为等腰三角形.25. 现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求: , 该抛物线的顶点P到的距离为. (1)、求满足设计要求的抛物线的函数表达式;(2)、现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为 , 求点A、B的坐标.26. 我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图1中,△AOB的内角∠AOB与△COD的内角∠COD互为对顶角,则△AOB与△COD为“对顶三角形”,根据三角形内角和定理知“对顶三角形”有如下性质:∠A+∠B=∠C+∠D.
(1)、求满足设计要求的抛物线的函数表达式;(2)、现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为 , 求点A、B的坐标.26. 我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图1中,△AOB的内角∠AOB与△COD的内角∠COD互为对顶角,则△AOB与△COD为“对顶三角形”,根据三角形内角和定理知“对顶三角形”有如下性质:∠A+∠B=∠C+∠D. (1)、如图1,在“对顶三角形”△AOB与△OOD中,∠AOB=70°,则∠C+∠D=°.(2)、如图2,在△ABC中,AD、BE分别平分∠BAC和∠ABC,若∠C=60°,∠ADE比∠BED大6°,求∠BED的度数.
(1)、如图1,在“对顶三角形”△AOB与△OOD中,∠AOB=70°,则∠C+∠D=°.(2)、如图2,在△ABC中,AD、BE分别平分∠BAC和∠ABC,若∠C=60°,∠ADE比∠BED大6°,求∠BED的度数.