陕西省延安市2023年中考数学第一次模拟考试卷

试卷更新日期：2023-03-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 2.5的相反数是（）

A、2.5 B、-2.5 C、 $\frac{2}{5}$ D、 $- \frac{2}{5}$

查看试题解析
2. 如图，将木条a，b与c钉在一起，∠1＝85°，∠2＝45°，要使木条a与b平行，木条a按箭头方向旋转的度数至少是（）

A、15° B、25° C、35° D、40°

查看试题解析
3. 计算： $2 x \cdot (- 3 x^{2} y^{3}) =$ （）

A、 $6 x^{3} y^{3}$ B、 $- 6 x^{2} y^{3}$ C、 $- 6 x^{3} y^{3}$ D、 $18 x^{3} y^{3}$

查看试题解析
4. 如图，四边形ABCD的对角线互相平分，要使它成为矩形，那么需要添加的条件是（）

A、AB=BC B、AC垂直BD C、∠A=∠C D、AC=BD

查看试题解析
5. 已知二元一次方程组 ${\begin{array}{l} x - y = - 5 \\ x + 2 y = - 2 \end{array}$ 的解为 ${\begin{array}{l} x = - 4 \\ y = 1 \end{array}$ ，则在同一平面直角坐标系中，直线 $l_{1}$ ： $y = x + 5$ 与直线 $l_{2}$ ： $y = - \frac{1}{2} x - 1$ 的交点坐标为（）

A、 $(4 ， 1)$ B、 $(1 ， - 4)$ C、 $(- 1 ， - 4)$ D、 $(- 4 ， 1)$

查看试题解析
6. 如图， $△ A B C$ 内接于⊙ $O ， ∠ C = 46 °$ ，连接 $O A$ ，则 $∠ O A B =$ （）

A、 $44 °$ B、 $45 °$ C、 $54 °$ D、 $67 °$

查看试题解析
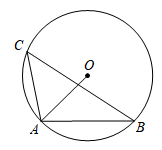7. 如图是四个二次函数的图象，则a、b、c、d的大小关系为（）

A、 $d < c < a < b$ B、 $d < c < b < a$ C、 $c < d < a < b$ D、 $c < d < b < a$

查看试题解析

二、填空题

8. $- π ， - 3 ， \sqrt[3]{3}$ 的大小顺序是（用“>”号连接）.

查看试题解析
9. 计算 $2^{5} \div 0 . 5^{- 4} - {(2 π - 6.28)}^{0}$ 的结果是.

查看试题解析
10. 比较大小： $\sqrt{10} - 4$ 0.（填“ $>$ ”、“ $<$ ”或“ $=$ ”）

查看试题解析
11. 数学中，把 $\frac{\sqrt{5} - 1}{2}$ 这个比例称为黄金分割比.鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例，是自然界最美的鬼斧神工.如图， $P$ 是 $A B$ 的黄金分割点 $(A P > B P)$ ，若线段 $A B$ 的长为 $8 c m$ ，则 $A P$ 的长为 $c m$ .

查看试题解析
12. 已知点A(−2，m)在一个反比例函数的图象上，点A′与点A关于y轴对称.若点A′在正比例函数 $y = \frac{1}{2} x$ 的图象上，则这个反比例函数的表达式为.

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A B = 2 \sqrt{3}$ ， $A D = 2$ ，点 $E$ 为线段 $C D$ 的中点，动点 $F$ 从点 $C$ 出发，沿 $C \to B \to A$ 的方向在 $C B$ 和 $B A$ 上运动，将矩形沿 $E F$ 折叠，点 $C$ 的对应点为 $C^{'}$ ，当点 $C^{'}$ 恰好落在矩形的对角线上时，点 $F$ 运动的距离为.

查看试题解析

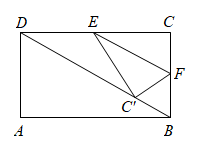
三、解答题

14. 计算： $\sqrt{2} \times \sqrt{8} + | - \sqrt{3} | - {(π - 3)}^{0}$ .

查看试题解析
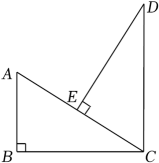
15. 解不等式组 ${\begin{array}{l} x - 3 (x - 2) > 4 \\ \frac{2 x - 1}{3} \geq \frac{3 x + 2}{6} - 1 \end{array}$ 并写出该不等式组的最小整数解．

查看试题解析
16. 化简： $(a + \frac{3 a b + b^{2}}{a - b}) \div \frac{a + b}{a - b}$ .

查看试题解析
17. 已知点 $A (2 a ， 3 a + 1)$ 是平面直角坐标系中的点.

(1)、若点A在第二象限的角平分线上，求a的值；

(2)、若点A在第三象限，且到两坐标轴的距离和为9，请确定点A的坐标.

查看试题解析
18. 如图，在Rt△ABC中，∠B＝90°，CD∥AB，DE⊥AC于点E，且CE＝AB．求证：△CED≌△ABC．

查看试题解析
19. 如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为 $A (1 ， 2) ， B (3 ， 1) ， C (- 2 ， - 1)$ .在图中作出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出点B、C的对应点 $B_{1}$ 、 $C_{1}$ 的坐标.

查看试题解析
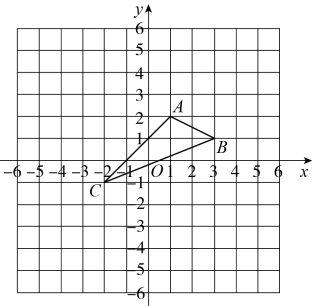20. 保护环境，人人有责，某校为培养学生“垃圾分类，从我做起”的环保意识，组织开展“游戏互动”､“趣味问答”､“模拟投放”三项活动（分别以 $A$ 、 $B$ 、 $C$ 来依次表示这三项活动）.活动开始前，将 $A$ ， $B$ ， $C$ 这三个字母分别写在三张无差别不透明的卡片正面上，洗匀后正面向下放在桌面上，小南同学先从中随机抽取一张卡片放回后洗匀，小晶同学从中再随机抽取一张卡片.

(1)、求小南抽到参加“趣味问答”活动的概率；

(2)、用列表法或画树状图法，求小南和小晶都抽到参加“趣味问答”活动的概率.

查看试题解析
21. 已知有一块三角形材料 $∠ A B C$ ，其中 $B C = 120 c m$ ，高 $A D = 80 c m$ ，现需要在三角形 $A B C$ 上裁下一个正方形材料做零件，使得正方形 $E F G H$ 的顶点 $E$ 、 $F$ 分别在边 $A B$ ， $A C$ 上， $H$ 、 $G$ 在 $B C$ 上，裁下的正方形 $E F G H$ 的边长是多少？

查看试题解析
22. 如图1，小明家、食堂、图书馆在同一条直线上，小明从食堂吃完早餐，接着骑自行车去图书馆读书，然后以相同的速度原路返回家.如图2中反映了小明离家的距离 $y (m)$ 与他所用时间 $x (m i n)$ 之间的函数关系.

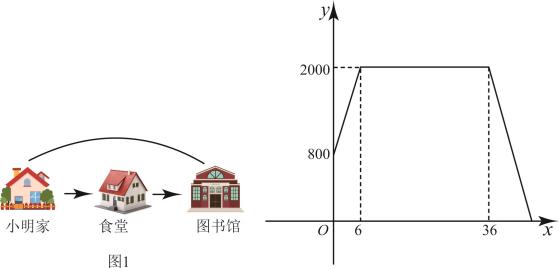(1)、小明家与图书馆的距离为 $m$ ，小明骑自行车速度为 $m / m i n$ ；

(2)、求小明从图书馆返回家的过程中， $y$ 与 $x$ 的函数解析式；

(3)、当小明离家的距离为 $1000 m$ 时，求 $x$ 的值.

查看试题解析
23. 为迎接党的二十大胜利召开，某校开展了以“不忘初心跟党走”为主题的读书活动，学校对本校学生9月份“读书量”进行了随机抽样调查，对所有随机抽取的数据进行了统计，并绘制成如下两幅不完整的统计图.

(1)、求出此次抽样调查的学生总数，并补全条形统计图；

(2)、本次所抽取学生9月份“读书量”的众数为本；

(3)、根据抽样调查的结果，请你估计该校1000名学生中，9月份“读书量”不少于4本的学生人数.

查看试题解析
24. 在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ， $A D$ 是 $△ A B C$ 的角平分线.

(1)、如图1，点E、F分别是线段 $C D$ 、 $A D$ 上的点，且 $D E = D F$ ， $A E$ 与 $B F$ 的延长线交于点G，则 $A E$ 与 $B F$ 的数量关系是，位置关系是；

(2)、如图2，点E、F分别在 $D C$ 和 $D A$ 的延长线上，且 $D E = D F$ ， $E A$ 的延长线交 $B F$ 于点G.
①（1）中的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由；
②连接 $D G$ ，若 $D G = 4 \sqrt{2}$ ， $D E = 6$ ，求 $E G$ 的长.

查看试题解析
25. 卡塔尔世界杯完美落幕.在一场比赛中，球员甲在离对方球门30米处的 $O$ 点起脚吊射（把球高高地挑过守门员的头顶，射入球门），假如球飞行的路线是一条抛物线，在离球门14米时，足球达到最大高度8米.如图所示，以球员甲所在位置 $O$ 点为原点，球员甲与对方球门所在直线为 $x$ 轴，建立平面直角坐标系.

(1)、求满足条件的抛物线的函数表达式；

(2)、如果葡萄牙球员 $C$ 罗站在球员甲前3米处， $C$ 罗跳起后最高能达到2.88米，那么 $C$ 罗能否在空中截住这次吊射？

查看试题解析
26. 如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为倍角三角形，并称这两个角的公共边为底边.

例如：若△ABC中，∠A＝2∠B，则△ABC为以边AB为底边的倍角三角形.

(1)、已知△ABC为倍角三角形，且 $∠ A B C ＝ 2 ∠ C$ .
①如图1，若BD为△ABC的角平分线，则图中相等的线段有，图中相似三角形有；
②如图2，若AC的中垂线交边BC于点E，连接AE，则图中等腰三角形有.

(2)、【问题解决】
如图3，现有一块梯形板材ABCD， $A D ∥ B C$ ， ∠A＝90°，AB＝48，BC＝132，AD＝68.工人师傅想用这块板材裁出一个△BCP型部件，使得点P在梯形ABCD的边上，且△BCP为以BC为底边的倍角三角形.工人师傅在这块板材上的作法如下：
①作BC的中垂线l交BC于点E；

②在BC上方的直线l上截取EF＝33，连接CF并延长，交AD于点P；

③连接BP，得△BCP.

1）请问，若按上述作法，裁得的△BCP型部件是否符合要求？请证明你的想法.

2）是否存在其它满足要求的△BCP？若存在，请画出图形并求出CP的长；若不存在，请说明理由.

查看试题解析