陕西省铜川市2023年中考数学第一次模拟考试卷
试卷更新日期:2023-03-08 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、3 B、-3 C、 D、12. 如图,将三角尺的直角顶点放在直尺的一边上, , , 则的度数等于( )
 A、 B、 C、 D、3. 下列计算不正确的是( )A、 B、 C、 D、4. 如图,AC、BD是四边形ABCD的两条对角线,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A、 B、 C、 D、3. 下列计算不正确的是( )A、 B、 C、 D、4. 如图,AC、BD是四边形ABCD的两条对角线,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( ) A、AC⊥BD B、AB=CD C、AB∥CD D、AC=BD5. 如图,在中,为斜边上的中线,过点D作 , 连接 , 若 , , 则的长为( )
A、AC⊥BD B、AB=CD C、AB∥CD D、AC=BD5. 如图,在中,为斜边上的中线,过点D作 , 连接 , 若 , , 则的长为( )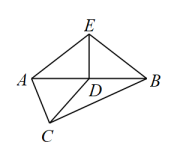 A、2 B、3 C、4 D、56. 如图,一次函数与的图象相交于点 , 则关于 , 的二元方程组的解是( )
A、2 B、3 C、4 D、56. 如图,一次函数与的图象相交于点 , 则关于 , 的二元方程组的解是( ) A、 B、 C、 D、7. 如图,点A是中优弧的中点, , C为劣弧上一点,则的度数是( )
A、 B、 C、 D、7. 如图,点A是中优弧的中点, , C为劣弧上一点,则的度数是( ) A、 B、 C、 D、8. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
A、 B、 C、 D、8. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:x
…
-2
0
1
3
…
y
…
6
-4
-6
-4
…
下列选项中,正确的是( )
A、这个函数的开口向下 B、这个函数的图象与x轴无交点 C、当时,y的值随x的增大而减小 D、这个函数的最小值小于6二、填空题
-
9. 计算:=10. 已知a、b、c在数轴上的位置如图所示,化简:
 11. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐到足底的长度之比约是黄金分割比.著名的“断臂维纳斯”便是如此.若某人的身体满足上述黄金分割比,且身高为175cm,则此人的肚脐到足底的长度约是(精确到1cm).12. 在平面直角坐标系中,等腰直角如图放置,其中 , 直角顶点A在反比例函数的图象上,若 , 则.
11. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐到足底的长度之比约是黄金分割比.著名的“断臂维纳斯”便是如此.若某人的身体满足上述黄金分割比,且身高为175cm,则此人的肚脐到足底的长度约是(精确到1cm).12. 在平面直角坐标系中,等腰直角如图放置,其中 , 直角顶点A在反比例函数的图象上,若 , 则.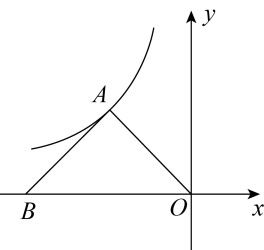 13. 中国结象征着中华民族的历史文化与精神,小贤家有一中国结挂饰,他想求两对边的距离,利用所学知识抽象出如图所示的菱形 , 测得 , 直线交两对边于点E,F,则的长为cm.
13. 中国结象征着中华民族的历史文化与精神,小贤家有一中国结挂饰,他想求两对边的距离,利用所学知识抽象出如图所示的菱形 , 测得 , 直线交两对边于点E,F,则的长为cm.
三、解答题
-
14. 计算:.15. 解不等式组:16. 化简:17. 如图,已知是的一个外角.请用尺规作图法,求作射线 , 使.(保留作图痕迹,不写作法)
 18. 如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.
18. 如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.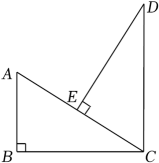 19. 如图,的顶点坐标分别为.将平移后得到 , 且点A的对应点是 , 点B、C的对应点分别是.
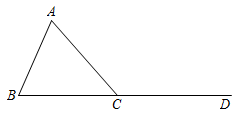
19. 如图,的顶点坐标分别为.将平移后得到 , 且点A的对应点是 , 点B、C的对应点分别是.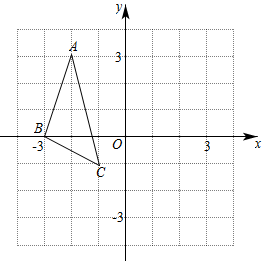 (1)、点A、之间的距离是;(2)、请在图中画出.20. 保护环境,人人有责,某校为培养学生“垃圾分类,从我做起”的环保意识,组织开展“游戏互动”、“趣味问答”、“模拟投放”三项活动(分别以、、来依次表示这三项活动).活动开始前,将 , , 这三个字母分别写在三张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,小南同学先从中随机抽取一张卡片放回后洗匀,小晶同学从中再随机抽取一张卡片.(1)、求小南抽到参加“趣味问答”活动的概率;(2)、用列表法或画树状图法,求小南和小晶都抽到参加“趣味问答”活动的概率.21. 已知有一块三角形材料 , 其中 , 高 , 现需要在三角形上裁下一个正方形材料做零件,使得正方形的顶点、分别在边 , 上,、在上,裁下的正方形的边长是多少?
(1)、点A、之间的距离是;(2)、请在图中画出.20. 保护环境,人人有责,某校为培养学生“垃圾分类,从我做起”的环保意识,组织开展“游戏互动”、“趣味问答”、“模拟投放”三项活动(分别以、、来依次表示这三项活动).活动开始前,将 , , 这三个字母分别写在三张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,小南同学先从中随机抽取一张卡片放回后洗匀,小晶同学从中再随机抽取一张卡片.(1)、求小南抽到参加“趣味问答”活动的概率;(2)、用列表法或画树状图法,求小南和小晶都抽到参加“趣味问答”活动的概率.21. 已知有一块三角形材料 , 其中 , 高 , 现需要在三角形上裁下一个正方形材料做零件,使得正方形的顶点、分别在边 , 上,、在上,裁下的正方形的边长是多少? 22. 如图,是一个“函数求值机”的示意图,其中y是x的函数.下面表格中,是通过该“函数求值机”得到的几组x与y的对应值.
22. 如图,是一个“函数求值机”的示意图,其中y是x的函数.下面表格中,是通过该“函数求值机”得到的几组x与y的对应值.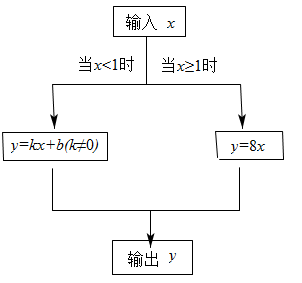
输人x
…
-6
-4
-2
0
2
…
输出y
…
-6
-2
2
6
16
…
根据以上信息,解答下列问题:
(1)、当输入的x值为1时,输出的y值为;(2)、求k,b的值;(3)、当输出的y值为0时,求输入的x值.23. 阳光中学积极开展课后廷时服务话动,提供了“有趣的生物实验,虚拟机器人竞赛,国际象棋大赛,趣味篮球训练,经典影视欣赏……”等课程供学生自由选择一个学期后,该校为了解学生对课后延时服务的满意情况,随机对部分学生进行问卷调查,并将调查结果按照“A.非常满意;B.比较满意;C.基本满意;D.不满意”四个等级绘制成了如图所示的两幅不完整的统计图.
请根据图中信息,解答下列问题:
(1)、该校抽样调查的学生人数为 ▲ 人,请补全条形统计图;(2)、样本中,学生对课后延时服务满意情况的“中位数”所在等级为 , “众数”所在等级为;(填“ , , 或”)(3)、若该校共有学生2000人,估计全校学生对课后延时服务满意的(包含 , , 三个等级)有多少人?24. 如图,是⊙的直径,是⊙的切线,、是⊙的弦,且 , 垂足为E,连接并延长,交于点P.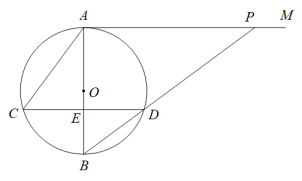 (1)、求证:;(2)、若⊙的半径 , 求线段的长.25. 现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求: , 该抛物线的顶点P到的距离为.
(1)、求证:;(2)、若⊙的半径 , 求线段的长.25. 现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求: , 该抛物线的顶点P到的距离为. (1)、求满足设计要求的抛物线的函数表达式;(2)、现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为 , 求点A、B的坐标.26. 如图:
(1)、求满足设计要求的抛物线的函数表达式;(2)、现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为 , 求点A、B的坐标.26. 如图: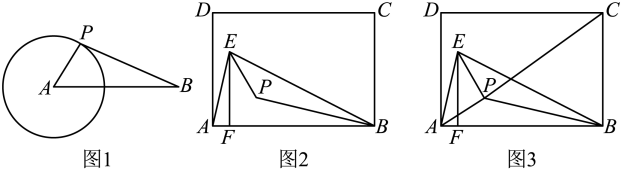 (1)、如图1,的半径为2, , 点为上任意一点,则的最小值为.(2)、如图2,已知矩形 , 点为上方一点,连接 , , 作于点 , 点是的内心,求角的度数.(3)、如图3,在(2)的条件下,连接 , , 若矩形的边长 , , , 求此时的最小值.
(1)、如图1,的半径为2, , 点为上任意一点,则的最小值为.(2)、如图2,已知矩形 , 点为上方一点,连接 , , 作于点 , 点是的内心,求角的度数.(3)、如图3,在(2)的条件下,连接 , , 若矩形的边长 , , , 求此时的最小值.