海南省儋州市2023年中考数学第一次模拟试题
试卷更新日期:2023-03-08 类型:中考模拟
一、单选题
-
1. 若非零数 , 互为相反数,下列四组数中,互为相反数的个数为( )
①与;②与;③与;④与
A、0 B、1 C、2 D、32. 成人体内成熟的红细胞的平均直径一般为0.000007245m,数0.000007245用科学记数法表示( )A、 B、 C、 D、3. 如图是由6个相同的小立方块搭成的几何体,那么这个几何体从上面看是( )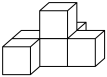 A、
A、 B、
B、 C、
C、 D、
D、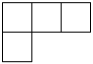 4. 关于x的一元一次不等式的解集为( )A、x B、x C、x D、x5. 如图,直线、被直线l所截, , , 则的大小为( )
4. 关于x的一元一次不等式的解集为( )A、x B、x C、x D、x5. 如图,直线、被直线l所截, , , 则的大小为( ) A、40° B、80° C、135° D、140°6. 小明用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:
A、40° B、80° C、135° D、140°6. 小明用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:步数(万步)
1.0
1.1
1.2
1.3
1.4
天数
3
3
9
11
4
在每天所走的步数这组数据中,众数和中位数分别是( )
A、1.3,1.25 B、1.3,1.3 C、1.4,1.3 D、1.3,1.17. 一个不透明的袋子中装有2个红球和若干个黄球,这些球除颜色外都相同.经过多次试验发现,摸出红球的频率稳定在左右,则袋子中的黄球个数最有可能是( )A、1 B、2 C、4 D、68. 如图,在平面直角坐标系中,的顶点在轴的正半轴上, , 点的坐标为 , 将绕点逆时针旋转,使点的对应点落在边上,连接、 , 则线段的长度是( ) A、1 B、2 C、 D、9. 反比例函数y=(k≠0)经过点(-2,4),则下列各点也在这个函数图象上的是( )A、(2,4) B、(-1,-8) C、(-2,-4) D、(4,-2)10. 的三边为 , , , 下列条件不能确保为直角三角形的是( )A、 B、 C、 D、11. 小杰在一个高为的建筑物顶端,测得一根高出此建筑物的旗杆顶端的仰角为 , 旗杆与地面接触点的俯角为 , 那么该旗杆的高度是( )A、 B、 C、 D、12. 如图,已知D、E分别是的边、的中点,是的中线,连接、、 , 若的面积为40,则阴影部分的面积为( )
A、1 B、2 C、 D、9. 反比例函数y=(k≠0)经过点(-2,4),则下列各点也在这个函数图象上的是( )A、(2,4) B、(-1,-8) C、(-2,-4) D、(4,-2)10. 的三边为 , , , 下列条件不能确保为直角三角形的是( )A、 B、 C、 D、11. 小杰在一个高为的建筑物顶端,测得一根高出此建筑物的旗杆顶端的仰角为 , 旗杆与地面接触点的俯角为 , 那么该旗杆的高度是( )A、 B、 C、 D、12. 如图,已知D、E分别是的边、的中点,是的中线,连接、、 , 若的面积为40,则阴影部分的面积为( ) A、10 B、5 C、8 D、4
A、10 B、5 C、8 D、4二、填空题
-
13. 分解因式:.14. 如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠CBG=.
 15. 如图,△ABC与△A′B′C′关于直线l对称,则∠B的度数为 .
15. 如图,△ABC与△A′B′C′关于直线l对称,则∠B的度数为 .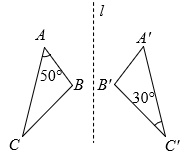 16. 用火柴棒按如图的方式摆出一系列图案,按这种方式摆下去,第个图案所用的火柴棒的根数为.
16. 用火柴棒按如图的方式摆出一系列图案,按这种方式摆下去,第个图案所用的火柴棒的根数为.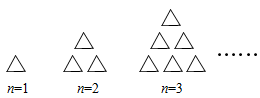
三、解答题
-
17. 已知 , 求下列代数式的值.(1)、;(2)、.18. 阅读理解:
为打造陶子河沿岸的风景带,有一段长为360米的河道整治任务由A、B两个工程队先后接力完成,A工程队每天整治24米,B工程队每天整治16米,共用20天.
(1)、根据题意,甲乙两个同学分别列出了尚不完整的方程组如下:甲: 乙:
根据甲、乙两名同学所列的方程组,请你分别指出未知数 , 表示的意义,并且补全甲、乙两名同学所列的方程组:
甲:表示 ▲ , 表示 ▲ ;
乙:表示 ▲ , 表示 ▲ ;
(2)、求出其中一个方程组的解,并回答A、B两工程队分别整治河道多少米?19. 某社区从不同住宅楼中随机选取了200名居民,调查社区居民双休日的学习状况,并将得到的数据制成扇形统计图(如图①)和频数分布直方图(如图②).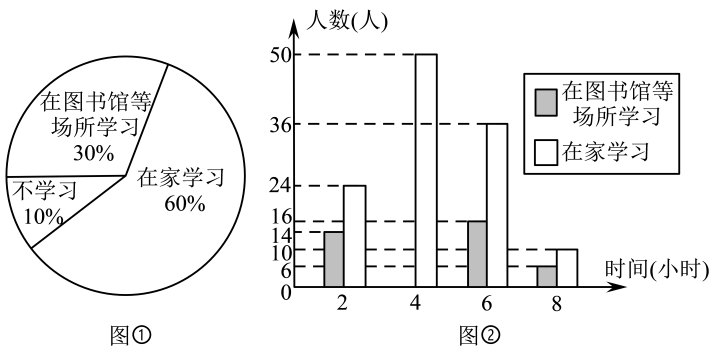 (1)、在这个调查中,200名居民双休日在家学习的有人;(2)、在这个调查中,在图书馆等场所学习的居民学习时间的平均数和众数分别是多少?(3)、估计该社区2000名居民双休日学习时间不少于4小时的人数.20. 如图,在坡顶A处的同一水平面上有一座古塔 , 数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为 , 然后他们沿着坡度为的斜坡攀行了26米到达点A,在坡顶A处又测得该塔的塔顶B的仰角为.
(1)、在这个调查中,200名居民双休日在家学习的有人;(2)、在这个调查中,在图书馆等场所学习的居民学习时间的平均数和众数分别是多少?(3)、估计该社区2000名居民双休日学习时间不少于4小时的人数.20. 如图,在坡顶A处的同一水平面上有一座古塔 , 数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为 , 然后他们沿着坡度为的斜坡攀行了26米到达点A,在坡顶A处又测得该塔的塔顶B的仰角为.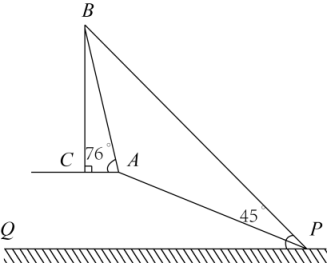 (1)、求坡顶A到地面的距离;(2)、计算古塔的高度(结果精确到1米).(参考数据: , , )21. 是边长为4的等边三角形,是等腰三角形, , , 以F为顶点作一个60°的角,角的两边分别交射线CA,BC于点D、E两点,连接DE.
(1)、求坡顶A到地面的距离;(2)、计算古塔的高度(结果精确到1米).(参考数据: , , )21. 是边长为4的等边三角形,是等腰三角形, , , 以F为顶点作一个60°的角,角的两边分别交射线CA,BC于点D、E两点,连接DE. (1)、如图1,若D、E两点在线段CA,BC的延长线上.
(1)、如图1,若D、E两点在线段CA,BC的延长线上.①求证:;
②试写出线段AD、BE、DE之间的数量关系,并说明理由;
(2)、如图2,若D、E两点在线段CA,BC上,求的周长.22. 如图,在直角坐标系中有 , 为坐标原点, , , 将此三角形绕原点顺时针旋转 , 得到 , 二次函数的图象刚好经过 , , 三点. (1)、求二次函数的解析式及顶点的坐标;(2)、过定点的直线与二次函数图象相交于M,两点.
(1)、求二次函数的解析式及顶点的坐标;(2)、过定点的直线与二次函数图象相交于M,两点.①若 , 求的值;
②证明:无论为何值,恒为直角三角形;
③当直线绕着定点旋转时,外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.