福建省福州市2022-2023学年九年级上学期适应性练习数学试卷
试卷更新日期:2023-03-08 类型:中考模拟
一、单选题
-
1. 地铁标志作为城市地铁的形象和符号,是城市文化的缩影,下列图案分别为北京,上海,深圳,福州四个城市的地铁标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列成语所描述的事件属于不可能事件的是( )A、守株待兔 B、水中捞月 C、水滴石穿 D、百发百中3. 下列图形中,正多边形内接于半径相等的圆,其中正多边形周长最小的是( )A、
2. 下列成语所描述的事件属于不可能事件的是( )A、守株待兔 B、水中捞月 C、水滴石穿 D、百发百中3. 下列图形中,正多边形内接于半径相等的圆,其中正多边形周长最小的是( )A、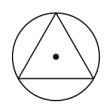 B、
B、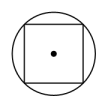 C、
C、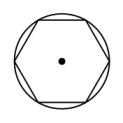 D、
D、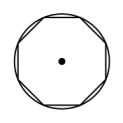 4. 如图,已知直线直线和分别与直线 , , 交于点A,B,C和点D,E,F,若 , , 则的长是( )
4. 如图,已知直线直线和分别与直线 , , 交于点A,B,C和点D,E,F,若 , , 则的长是( )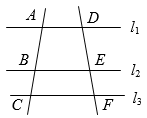 A、 B、3 C、6 D、95. 方程的解是( )A、 , B、 , C、 , D、 ,6. 如图,将点M绕点O顺时针旋转90°得到点N,则点N在( )
A、 B、3 C、6 D、95. 方程的解是( )A、 , B、 , C、 , D、 ,6. 如图,将点M绕点O顺时针旋转90°得到点N,则点N在( )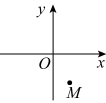 A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 将抛物线向左平移1个单位长度,平移后的抛物线的解析式是( )A、 B、 C、 D、8. 2020年教育部印发了《大中小学劳动教育指导纲要(试行)》,劳动教育已纳入人才培养过程.某中学加大校园农场建设,为学生提供更多的劳动场所.该农场某种作物2020年的年产量为100千克,2022年的年产量为225千克,设该作物年产量的平均增长率为x,则符合题意的方程是( )A、 B、 C、 D、9. 关于x的一元二次方程 , 若 , 则该方程必有一个根是( )A、 B、 C、 D、10. 公元前3世纪,古希腊科学家阿基米德发现了“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂,当用撬棍撬动一块石头时,发现阻力和阻力臂分别为和 , 关于动力F和动力臂l,下列说法错误的是( )A、F与l的积为定值 B、F随l的增大而减小 C、当l为时,撬动石头至少需要的力 D、F关于l的函数图象位于第一、第三象限
A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 将抛物线向左平移1个单位长度,平移后的抛物线的解析式是( )A、 B、 C、 D、8. 2020年教育部印发了《大中小学劳动教育指导纲要(试行)》,劳动教育已纳入人才培养过程.某中学加大校园农场建设,为学生提供更多的劳动场所.该农场某种作物2020年的年产量为100千克,2022年的年产量为225千克,设该作物年产量的平均增长率为x,则符合题意的方程是( )A、 B、 C、 D、9. 关于x的一元二次方程 , 若 , 则该方程必有一个根是( )A、 B、 C、 D、10. 公元前3世纪,古希腊科学家阿基米德发现了“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂,当用撬棍撬动一块石头时,发现阻力和阻力臂分别为和 , 关于动力F和动力臂l,下列说法错误的是( )A、F与l的积为定值 B、F随l的增大而减小 C、当l为时,撬动石头至少需要的力 D、F关于l的函数图象位于第一、第三象限二、填空题
-
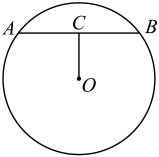
11. 若反比例函数的图象经过点 , 则k的值是.12. 如图,在中,弦 , , 垂足为C, , 则的半径为.
 13. 某林业部门要考察某种幼树在一定条件下的移植成活率,在同样条件下,对这种幼树进行大量移植,并完成统计情况,得到一组统计数据:
13. 某林业部门要考察某种幼树在一定条件下的移植成活率,在同样条件下,对这种幼树进行大量移植,并完成统计情况,得到一组统计数据:移植总次数n
1500
3500
7000
9000
14000
成活数m
1335
3203
6335
8037
12628
成活的频率
估计该种幼树在此条件下移植成活的概率是(结果精确到0.1).
14. 在半径为1的圆中,圆心角所对的弧长是.15. 某足球运动员将足球沿与地面成一定角度的方向踢出,如果不考虑空气阻力,足球飞行的高度h(单位:m)与足球飞行的时间t(单位:s)之间具有二次函数关系,其部分图象如图所示,则足球从踢出到落地所需的时间是.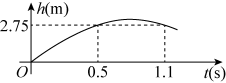 16. 已知内接于⊙O,I是的内心,若 , 则的度数是.
16. 已知内接于⊙O,I是的内心,若 , 则的度数是.三、解答题
-
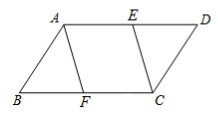
17. 解方程: .18. 如图,在中,点E,F分别在边 , 上,且 , 连接 , , 求证:四边形是中心对称图形.
 19. 已知一元二次方程有两个不相等的实数根,求a的取值范围.20. 如图,将绕点A顺时针旋转得到(为锐角),点D与点B对应,连接 , .求证:.
19. 已知一元二次方程有两个不相等的实数根,求a的取值范围.20. 如图,将绕点A顺时针旋转得到(为锐角),点D与点B对应,连接 , .求证:.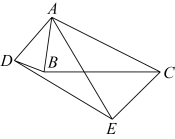 21. 为增强学生爱国意识,激发爱国情怀,某校9月开展了“喜迎二十大、永远跟党走、奋进新征程”主题教育活动,活动方式有:A.主题征文,B.书法绘画,C.红歌传唱,D.经典诵读.为了解最受学生喜爱的活动方式,现随机抽取若干名学生进行调查,并将调查结果绘制成如下两幅不完整的统计图.
21. 为增强学生爱国意识,激发爱国情怀,某校9月开展了“喜迎二十大、永远跟党走、奋进新征程”主题教育活动,活动方式有:A.主题征文,B.书法绘画,C.红歌传唱,D.经典诵读.为了解最受学生喜爱的活动方式,现随机抽取若干名学生进行调查,并将调查结果绘制成如下两幅不完整的统计图.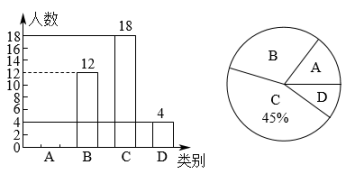
根据以上信息,解答下列问题:
(1)、参与此次抽样调查的学生人数是 , 扇形统计图中A部分圆心角的度数是;(2)、学校从1班,2班,3班,4班中随机选取两个班参加“红歌传唱”的活动,求恰好选中2班和3班的概率.22. 如图,P为外一点,M为中点.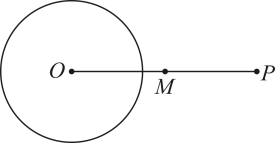 (1)、过点P作的一条切线 , 且Q为切点(尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,若 , 求证:点M在上.23. 如图,一块余料 , , , , , , 且和之间的距离为4.以所在直线为x轴,长为1个单位长度,建立适当的平面直角坐标系,图中曲线恰好是该平面直角坐标系中反比例函数图象的一部分.
(1)、过点P作的一条切线 , 且Q为切点(尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,若 , 求证:点M在上.23. 如图,一块余料 , , , , , , 且和之间的距离为4.以所在直线为x轴,长为1个单位长度,建立适当的平面直角坐标系,图中曲线恰好是该平面直角坐标系中反比例函数图象的一部分.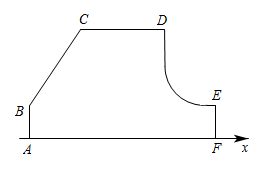 (1)、补全该平面直角坐标系,并写出点B,C,D,E的坐标;(2)、李师傅想利用该余料截取一块矩形材料 , 其中边在上(点P在点Q的右侧),其余两个顶点M与N分别在线段与曲线段上,求所截取的矩形材料面积的最大值.24. 在中, , 两条高 , 交于点H,F是的中点,连接并延长交边于点G.
(1)、补全该平面直角坐标系,并写出点B,C,D,E的坐标;(2)、李师傅想利用该余料截取一块矩形材料 , 其中边在上(点P在点Q的右侧),其余两个顶点M与N分别在线段与曲线段上,求所截取的矩形材料面积的最大值.24. 在中, , 两条高 , 交于点H,F是的中点,连接并延长交边于点G.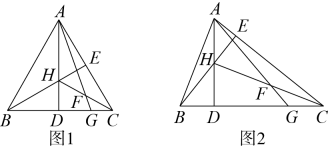 (1)、如图1,若是等边三角形.
(1)、如图1,若是等边三角形.①求证:;
②求的长.
(2)、如图2,若 , , 求的面积.25. 已知抛物线与轴的正半轴交于点 , 与轴交于点 , 当时,抛物线最低点的纵坐标为-4:当时,抛物线最低点的纵坐标为-3.(1)、求 , 的关系式(用含的代数式表示);(2)、若 , 求抛物线的解析式;(3)、在(2)的条件下,为抛物线对称轴上一点,过点的直线交抛物线于 , 两点,为线段的中点,过点作轴的垂线,交抛物线于点 , 探究是否存在定点 , 使得总成立,若存在,求出点的坐标:若不存在,请说明理由.