黑龙江省双鸭山市宝清县2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-07 类型：期中考试

进入出卷网下载

一、单选题

1. 2022年，在中国举办了第二十四届冬季奥林匹克运动会，图中是吉祥物“冰墩墩”，将图中的“冰墩墩”通过平移可以得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. $\sqrt[3]{8}$ 的算术平方根是（　　）

A、2 B、±2 C、 $\sqrt{2}$ D、± $\sqrt{2}$

查看试题解析
3. 如图，直线 $A B ∥ C D$ ， ∠2=50°，则∠1的度数是（）

A、120° B、110° C、140° D、130°

查看试题解析
4. 在平面直角坐标系中，已知点 $A (- 2 ， 3)$ ， $B (4 ， 3)$ ，则A，B两点之间的距离为（）

A、4 B、5 C、6 D、10

查看试题解析
5. 如图，将三角形纸板ABC沿直线AB向右平行移动，使△CAB到达△DBE的位置，若∠CAB=50°，∠ABC=100°，则∠CBE的度数为（）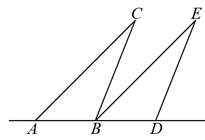

A、50° B、40° C、30° D、110°

查看试题解析
6. 下列命题中是真命题的是（）

A、若 $| x | = 3$ ，则x＝3 B、平行于同一条直线的两条直线平行 C、一个锐角与一个钝角的和等于一个平角 D、同位角相等

查看试题解析
7. 已知点 $A (a - 5 ， 2 b - 1)$ 在y轴上，点 $B (3 a + 2 ， b + 3)$ 在x轴上，则点 $C (a ， b)$ 的坐标为（）

A、 $(5 ， - 3)$ B、 $(- 5 ， 3)$ C、 $(- 5 ， - 3)$ D、 $(5 ， 3)$

查看试题解析
8. 若 $\sqrt{x - 5} + | y + 25 | = 0$ ，则 $\sqrt[3]{x y}$ 的值为（）

A、5 B、15 C、25 D、－5

查看试题解析
9. 如图摆放的一副学生用直角三角板， $∠ F = 30^{\circ} ， ∠ C = 45^{\circ}$ ， $A B$ 与 $D E$ 相交于点G，当 $E F // B C$ 时， $∠ E G B$ 的度数是（）

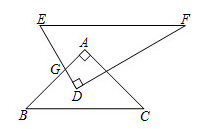A、135° B、120° C、115° D、105°

查看试题解析
10. 如图，AB//CD，OP⊥CD，OE平分∠BOC，OF⊥OE，∠OCD＝50°．下列结论：①∠COE＝65°；②OF平分∠AOC；③∠AOF＝∠POE；④∠POC＝2∠AOF．其中结论正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知一个正数的平方根为－3与2a－5，则a＝．

查看试题解析
12. 将命题“在同一平面内，垂直于同一条直线的两条直线平行”改写为“如果……，那么……”的形式为.

查看试题解析
13. 如图，有一个数值转换器：
当输入x＝625时，输出的y等于．

查看试题解析
14. 将点A（x，-2）向上平移3个单位，再向左平移2个单位，得到点B（1，y），则 $\sqrt{x + y}$ ＝．

查看试题解析
15. 定义新运算：对于a，b有 $a ☆ b = \sqrt{a} - \sqrt[3]{b}$ ，如 $4 ☆ (- 27) = \sqrt{4} - \sqrt[3]{- 27} = 2 + 3 = 5$ ，根据定义新运算，计算： $9 ☆ (- 125) =$ ．

查看试题解析
16. 如图，AO⊥BO，CO⊥DO，∠AOC＝75°，则∠BOD＝．

查看试题解析
17. 如图，点A，B的坐标分别为 $(3 ， 0)$ ， $(0 ， 2)$ ，若将线段AB平移至 $A_{1} B_{1}$ ，则a＋b的值为．

查看试题解析
18. 设 $\sqrt{6}$ 的整数部分为m， $\sqrt{17}$ 的整数部分为n，则m＋n＝．

查看试题解析
19. 如图所示，已知DE//BC，∠ABC＝100°，点F在射线BA上，且∠EDF＝120°，则∠DFB的度数为．

查看试题解析
20. 如图，动点P在平面直角坐标系xOy中，按图中箭头所示方向运动，第1次从原点到点 $(1 ， 2)$ ，第2次接着运动到点 $(2 ， 0)$ ，第3次接着运动到点 $(3 ， 1)$ ，第4次接着运动到点 $(4 ， 0)$ ……按这样的运动规律，经过第2023次运动后，动点P的坐标是．

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt[3]{- 8} - \sqrt{\frac{1}{9}} + \sqrt[3]{1 - \frac{63}{64}}$ ；

(2)、 $\sqrt{81} + \sqrt[3]{- 64} + | 2 - \sqrt{3} | + \sqrt{3}$ ．

查看试题解析
22. 求下列各式中x的值：

(1)、 $3 {(5 x + 1)}^{2} - 48 = 0$ ；

(2)、 $2 {(x - 1)}^{3} = - \frac{125}{4}$ ．

查看试题解析
23. 已知点 $P (2 x - 6 ， 3 x + 1)$ ，求下列情形下点P的坐标．

(1)、点P到x轴、y轴的距离相等，且点P在第二象限；

(2)、点P在过点 $A (2 ， - 4)$ 且与y轴平行的直线上．

查看试题解析
24. 如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD．

(1)、若∠BOD＝40°，求∠EOF的度数；

(2)、若 $∠ A O C = \frac{1}{4} ∠ E O D$ ，求∠AOC的度数．

查看试题解析
25. 已知：a是 $8 + \sqrt{15}$ 的小数部分，b是 $8 - \sqrt{15}$ 的小数部分．

(1)、求a、b的值；

(2)、求4a+4b+5的平方根．

查看试题解析
26. 如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为（﹣5，4）、（﹣3，0）、（0，2）．

(1)、画出三角形ABC，并求其面积；

(2)、如图，△A′B′C′是由△ABC经过怎样的平移得到的？

(3)、已知点P（a，b）为△ABC内的一点，则点P在△A′B′C′内的对应点P′的坐标为（，）．

查看试题解析
27. 如图，已知AB//CD．

(1)、如图①，EF分别和AB，CD相交于点E，F，求证∠1＝∠2；

(2)、如图②，试猜想∠1，∠2，∠EFD之间有什么数量关系，并证明你的结论；

(3)、如图③，若FH⊥AB于点E，∠1＝40°，求∠EFD的度数．

查看试题解析
28. 如图，在平面直角坐标系中， $A (0 ， a)$ ， $C (b ， 3)$ ，且满足 $| a + 3 | + \sqrt{b - 3} = 0$ ，过点C作CB⊥y轴于点B，连接AC，动点P从点B出发沿射线BC以每秒1个单位长度的速度运动（点P不与点C重合），设运动的时间为t秒，

(1)、求a，b的值；

(2)、设△APC的面积为S，用含t的式子表示S，并写出t的取值范围；

(3)、在x轴上是否存在点M，使△ABM的面积等于△ABC的面积的2倍？若存在，请直接写出点M的坐标，若不存在，请说明理由．

查看试题解析